Сила между магнитами

Магниты оказывают друг на друга силы и крутящие моменты посредством взаимодействия своих магнитных полей . Силы притяжения и отталкивания являются результатом этих взаимодействий. Магнитное поле каждого магнита создается микроскопическими токами электрически заряженных электронов, вращающихся вокруг ядер, и собственным магнетизмом фундаментальных частиц (таких как электроны), из которых состоит материал. Оба они довольно хорошо моделируются как крошечные петли тока, называемые магнитными диполями , которые создают собственное магнитное поле и подвергаются воздействию внешних магнитных полей. Самая элементарная сила между магнитами — это магнитное диполь-дипольное взаимодействие . Если известны все магнитные диполи для каждого магнита, то результирующую силу, действующую на оба магнита, можно определить путем суммирования всех взаимодействий между диполями первого магнита и диполями второго магнита.

Часто удобнее моделировать силу между двумя магнитами, возникающую из-за сил между магнитными полюсами, по которым распределены магнитные заряды . Положительный и отрицательный магнитный заряд всегда соединены нитью намагниченного материала; изолированного магнитного заряда не существует. Эта модель хорошо работает для прогнозирования сил между простыми магнитами, где доступны хорошие модели распределения магнитного заряда.

Магнитные полюса против атомных токов

Основная статья: магнитные полюса против атомных токов

Модель магнитного полюса для H и модель петли Ампера для B дают идентичное поле вне магнита. Внутри они очень разные.

Поле магнита представляет собой сумму полей всех намагниченных элементов объема, состоящих из небольших магнитных диполей на атомном уровне. Прямое суммирование всех этих дипольных полей требует трехмерного интегрирования для получения поля одного магнита, что может быть сложным.

Для однородной намагниченности проблему можно упростить двумя разными способами, используя теорему Стокса . При интегрировании по направлению намагничивания все диполи вдоль линии интегрирования нейтрализуют друг друга, за исключением торцевой поверхности магнита. Тогда поле возникает только из этих (математических) магнитных зарядов, распределенных по торцам магнита. Напротив, при интегрировании по намагниченной области, ортогональной направлению намагничивания, диполи внутри этой области нейтрализуют друг друга , за исключением внешней поверхности магнита, где они (математически) суммируются до кольцевого тока. Это называется моделью петли Ампера. В обеих моделях необходимо учитывать только двумерные распределения по поверхности магнита, что проще, чем исходная трехмерная задача.

Модель магнитного полюса : В модели магнитного полюса предполагается, что поверхности полюса постоянного магнита покрыты так называемым магнитным зарядом , частицы северного полюса на северном полюсе и частицы южного полюса на южном полюсе, которые являются источником линий магнитного поля. Поле, обусловленное магнитными зарядами, получается по закону Кулона с магнитными зарядами вместо электрических. Если известно распределение магнитных полюсов, то модель магнитного полюса дает точное распределение напряженности магнитного поля H как внутри, так и снаружи магнита. Распределение поверхностного заряда однородно, если магнит намагничен однородно и имеет плоские торцевые грани (например, цилиндр или призма).

Модель петли Ампера : В модели петли Ампера вся намагниченность обусловлена ​​эффектом микроскопических или атомных круговых связанных токов , также называемых токами Ампера во всем материале. Конечным эффектом этих микроскопических связанных токов является то, что магнит ведет себя так, как будто макроскопический электрический ток в петлях магнита течет с магнитным полем, нормальным к петлям. Поле, обусловленное такими токами, получается посредством закона Био-Савара . Модель петли Ампера дает правильную плотность магнитного потока B как внутри, так и снаружи магнита. Иногда бывает сложно рассчитать амперовы токи на поверхности магнита.

Магнитный дипольный момент

Основная статья: Магнитный дипольный момент

Вдали от магнита его магнитное поле почти всегда описывается (с хорошим приближением) дипольным полем, характеризуемым его полным дипольным моментом магнитным m . Это верно независимо от формы магнита, если магнитный момент отличен от нуля. Одной из характеристик дипольного поля является то, что напряженность поля падает обратно пропорционально кубу расстояния от центра магнита.

Таким образом, магнитный момент магнита является мерой его силы и ориентации. Петля электрического тока , стержневой магнит , электрон , молекула и планета — все они имеют магнитные моменты. Точнее, термин «магнитный момент» системы обычно относится к магнитному дипольному моменту , который создает первый член в мультипольном разложении. общего магнитного поля.

И крутящий момент, и сила, действующая на магнит со стороны внешнего магнитного поля, пропорциональны магнитному моменту этого магнита. Магнитный момент — это вектор : он имеет как величину, так и направление. Направление магнитного момента указывает с южного на северный полюс магнита (внутри магнита). Например, направление магнитного момента стержневого магнита, например, в компасе , — это направление, в котором указывают северные полюса.

В физически корректной модели петли Ампера магнитные дипольные моменты возникают из-за бесконечно малых петель тока. Для достаточно маленькой петли тока I и площади A магнитный дипольный момент равен: $$\mathbf {m} =I\mathbf {A} ,$$ где направление m нормально правила к площади в направлении, определенном с использованием тока и правой руки . Таким образом, в системе СИ единицей магнитного дипольного момента является амперметр . ² . Точнее, для учета многовитковых соленоидов единицей магнитного дипольного момента является ампер-витковый метр. ² .

В модели магнитного полюса магнитный дипольный момент обусловлен двумя равными и противоположными магнитными зарядами, разделенными расстоянием d . В этой модели m аналогичен электрическому дипольному моменту p, обусловленному электрическими зарядами: $$m=q_{\mathrm {m} }d,$$ где q _m — «магнитный заряд». Направление магнитного дипольного момента указывает от отрицательного южного полюса к положительному северному полюсу этого крошечного магнита.

Магнитная сила из-за неоднородного магнитного поля

Вершина: $\mathbf {B}$, сила, действующая на северные магнитные полюса.
Нижний: $\mathbf {\nabla } |\mathbf {B} |$, сила, действующая на выровненные диполи, такие как частицы железа.

Магниты рисуются по градиенту магнитного поля. Самый простой пример – притяжение противоположных полюсов двух магнитов. Каждый магнит создает магнитное поле, которое сильнее вблизи его полюсов. Если противоположные полюса двух отдельных магнитов обращены друг к другу, каждый из магнитов втягивается в более сильное магнитное поле рядом с полюсом другого. Однако если одинаковые полюса обращены друг к другу, они отталкиваются от большего магнитного поля.

Модель магнитного полюса предсказывает правильную математическую форму этой силы, и ее легче понять качественно. Ведь если магнит поместить в однородное магнитное поле, то оба полюса будут испытывать одинаковую магнитную силу, но в противоположных направлениях, поскольку они имеют противоположный магнитный заряд. Но когда магнит помещен в неоднородное поле, например, из-за другого магнита, полюс, испытывающий большое магнитное поле, будет испытывать большую силу, и на магнит будет действовать результирующая сила. Если магнит выровнен по магнитному полю, что соответствует двум магнитам, ориентированным в одном направлении вблизи полюсов, то он будет втянут в большее магнитное поле. Если он ориентирован противоположно, как в случае двух магнитов с одинаковыми полюсами, обращенными друг к другу, то магнит будет отталкиваться от области более сильного магнитного поля.

В модели петли Ампера на магнитный диполь также действует сила из-за неоднородного магнитного поля, но это связано с силами Лоренца в токовой петле, составляющей магнитный диполь. Сила, полученная в случае модели с токовой петлей, равна $$\mathbf {F} =\nabla \left(\mathbf {m} \cdot \mathbf {B} \right),$$ где градиент ∇ это изменение величины m · B на единицу расстояния, а направление — направление максимального увеличения m · B. — Чтобы понять это уравнение, обратите внимание, что скалярное произведение m · B = mB cos( θ ) , где m и B представляют собой величину θ между — угол векторов m и B, а ними . Если m находится в том же направлении, что и B, то скалярное произведение положительно, и точки градиента «вверх» тянут магнит в области с более высоким B-полем (точнее, с большим m · B ). B представляет силу и направление магнитного поля. Это уравнение справедливо только для магнитов нулевого размера, но часто является хорошим приближением для не слишком больших магнитов. Магнитная сила на более крупных магнитах определяется путем разделения их на более мелкие области, имеющие собственное значение m, а затем суммирования сил, действующих на каждую из этих областей.

Модель магнитного полюса

Модель магнитного полюса предполагает, что магнитные силы между магнитами возникают из-за магнитных зарядов вблизи полюсов. Эта модель работает даже вблизи магнита, когда магнитное поле становится более сложным и более зависимым от детальной формы и намагниченности магнита, а не только от вклада магнитного диполя. Формально поле можно выразить как мультипольное разложение : дипольное поле плюс квадрупольное поле плюс октопольное поле и т. д. в модели петли Ампера, но это может быть очень громоздко математически.

Расчет магнитной силы

Расчет силы притяжения или отталкивания между двумя магнитами в общем случае является очень сложной операцией, так как зависит от формы, намагниченности, ориентации и расстояния между магнитами. Модель магнитного полюса действительно зависит от некоторых знаний о том, как «магнитный заряд» распределяется по магнитным полюсам. Даже в этом случае он действительно полезен только для простых конфигураций. К счастью, это ограничение охватывает множество полезных случаев.

Сила между двумя магнитными полюсами

Если оба полюса достаточно малы, чтобы их можно было представить в виде отдельных точек, их можно рассматривать как точечные магнитные заряды. Классически сила между двумя магнитными полюсами определяется выражением:

$$F={{\mu q_{m1}q_{m2}} \over {4\pi r^{2}}}$$ где

• F — сила (единица СИ: ньютон )
• q _{m 1} и q _{m 2} — величины магнитного заряда на магнитных полюсах (единица СИ: ампер - метр ).
• μ — проницаемость промежуточной среды (единицы СИ: тесла -метр на ампер , генри на метр или ньютон на ампер в квадрате)
• r — расстояние (единица СИ: метр).

Описание полюса полезно практикующим магнетистам, проектирующим реальные магниты, но настоящие магниты имеют более сложное распределение полюсов, чем отдельные север и юг. Поэтому реализация идеи полюса непроста. В некоторых случаях одна из более сложных формул, приведенных ниже, будет более полезной.

Сила между двумя близлежащими намагниченными поверхностями области A

Механическую силу между двумя близлежащими намагниченными поверхностями можно рассчитать с помощью следующего уравнения. Уравнение справедливо только для случаев, когда влияние бахромы незначительно и объем воздушного зазора значительно меньше, чем у намагниченного материала, сила для каждой намагниченной поверхности равна: $$F={\frac {\mu _{0}H^{2}A}{2}}={\frac {B^{2}A}{2\mu _{0}}}$$ где:

• A — площадь каждой поверхности, м ²
• H — их намагничивающее поле , А/м.
• µ ₀ — проницаемость пространства , равная 4π×10 ⁻⁷ Т·м/А
• B — плотность потока , в Тл

Вывод этого уравнения аналогичен силе между двумя соседними электрически заряженными поверхностями: который предполагает, что поле между пластинами однородно.

Сила между двумя стержневыми магнитами

Поле двух притягивающих цилиндрических стержневых магнитов

Поле двух отталкивающихся цилиндрических стержневых магнитов

Сила между двумя одинаковыми цилиндрическими стержневыми магнитами, расположенными друг к другу на большом расстоянии. $x\gg R$ примерно: $$F\simeq \left[{\frac {B_{0}^{2}A^{2}\left(L^{2}+R^{2}\right)}{\pi \mu _{0}L^{2}}}\right]\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]$$ где

• B ₀ — плотность потока очень близко к каждому полюсу, в Т,
• A — площадь каждого столба, м. ² ,
• L — длина каждого магнита, м,
• R — радиус каждого магнита, м,
• x — расстояние между двумя магнитами, м

$$B_{0}={\frac {\mu _{0}}{2}}M$$ связывает плотность потока на полюсе с намагниченностью магнита.

Обратите внимание, что эти формулировки предполагают точечное распределение магнитного заряда вместо равномерного распределения по торцам, что является хорошим приближением только на относительно больших расстояниях. Для промежуточных расстояний численные методы необходимо использовать .

Сила между двумя цилиндрическими магнитами

Точная сила между двумя коаксиальными цилиндрическими стержневыми магнитами для нескольких соотношений сторон.

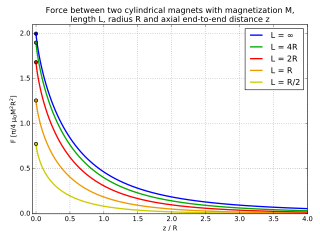
Для двух цилиндрических магнитов одинакового радиуса $R$и длины $L_{1}$ и $L_{2}$, и учитывая большой боковой зазор между ними, в пределе $x\gg R$, силу можно аппроксимировать выражением

$F(x,r)\simeq {\frac {\pi K_{d}}{2}}R^{4}\sum _{i,j=0}^{1}{\left({\frac {(-1)^{i+j}}{(x+iL_{1}+jL_{2})^{2}}}\left(1-{\frac {3}{2}}{\frac {r^{2}}{(x+iL_{1}+jL_{2})^{2}}}\right)\right)}$

где

• $R$ - радиус каждого из двух магнитов в предположении равенства радиусов
• $L_{1}$ длина первого магнита
• $L_{2}$ длина второго магнита
• $K_{d}$ - максимальный энергетический продукт в Дж/м. ³ (Джоули на кубический метр)
• $x$ нормальное расстояние между двумя параллельными гранями магнитов
• $r$ - расстояние между осями магнитных диполей двух магнитов.

Когда их магнитный диполь выровнен, силу можно вычислить аналитически с использованием эллиптических интегралов .

$$F(x)\simeq {\frac {\pi K_{d}}{2}}R^{4}\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]$$

Это можно переписать так:

$$F(x)\simeq {\frac {\pi \mu _{0}}{4}}M^{2}R^{4}\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]$$

Где $M$ намагниченность магнитов и $x$ это расстояние между ними. Для небольших значений $x$, результаты ошибочны, поскольку сила становится большой на расстоянии, близком к нулю.

Если магнит длинный ( $L\gg R$), измерение плотности магнитного потока очень близко к магниту $B_{0}$ примерно связано с $M$ по формуле $$B_{0}={\frac {\mu _{0}}{2}}M.$$

Эффективный магнитный дипольный момент можно записать как $$m=MV$$ где $V$ это объем магнита. Для цилиндра это $V=\pi R^{2}L$, и $M$ – поле намагничивания диполя.

Когда $L\ll x$ получено приближение точечного диполя, $$F(x)={\frac {3\pi \mu _{0}}{2}}M^{2}R^{4}L^{2}{\frac {1}{x^{4}}}={\frac {3\mu _{0}}{2\pi }}M^{2}V^{2}{\frac {1}{x^{4}}}={\frac {3\mu _{0}}{2\pi }}m_{1}m_{2}{\frac {1}{x^{4}}}$$

Что соответствует выражению силы между двумя магнитными диполями.

Модель петли Ампера

Французский ученый Андре Мари Ампер обнаружил, что магнетизм, создаваемый постоянными магнитами, и магнетизм, создаваемый электромагнитами, представляют собой один и тот же вид магнетизма. Поэтому силу постоянного магнита можно выразить теми же терминами, что и силу электромагнита.

Сила магнетизма электромагнита, представляющего собой плоскую проволочную петлю, по которой течет ток, измеренная на расстоянии, большом по сравнению с размером петли, пропорциональна этому току и площади поверхности этой петли. .

Чтобы выразить силу постоянного магнита в тех же терминах, что и электромагнита, постоянный магнит рассматривается так, как будто он содержит небольшие токовые петли по всему объему, и тогда магнитная сила этого магнита оказывается пропорциональной току каждой петли (в амперах), пропорционально поверхности каждой петли (в квадратных метрах) и пропорционально плотности токовых петель в материале (в единицах на кубический метр), поэтому размер прочности магнетизма постоянного магнита ампер, умноженный на квадратный метр на кубический метр, это ампер на метр.

Вот почему правильной единицей магнетизма является ампер на метр, хотя в постоянном магните этих небольших токовых петель на самом деле нет.

Справедливость модели Ампера означает, что можно думать о магнитном материале так, как будто он состоит из токовых петель, а общий эффект представляет собой сумму эффектов каждой токовой петли, и, следовательно, магнитный эффект настоящего магнита может быть вычислена как сумма магнитных эффектов крошечных кусочков магнитного материала, находящихся на расстоянии, большом по сравнению с размером каждого кусочка.

Это очень полезно для расчета магнитного силового поля настоящего магнита; Он включает в себя суммирование большого количества малых сил, и вам не следует делать это вручную, а пусть ваш компьютер сделает это за вас; Все, что нужно знать компьютерной программе, — это сила между маленькими магнитами, находящимися на большом расстоянии друг от друга.

В таких расчетах часто предполагается, что каждый небольшой кусочек магнитного материала (одного и того же размера) обладает одинаково сильным магнетизмом, но это не всегда верно: магнит, помещенный рядом с другим магнитом, может изменить намагниченность этого другого магнита. Для постоянных магнитов это обычно небольшое изменение, но если у вас есть электромагнит, состоящий из проволоки, намотанной на железный сердечник, и вы подносите постоянный магнит близко к этому сердечнику, то намагниченность этого сердечника может резко измениться (например, например, если в проводе нет тока, электромагнит не будет магнитным, но когда постоянный магнит приближается, сердечник электромагнита становится магнитным).

Таким образом, модель Ампера подходит для расчета магнитного силового поля постоянного магнита, но для электромагнитов лучше использовать подход магнитной цепи.

Магнитное диполь-дипольное взаимодействие

Основная статья: Магнитное диполь-дипольное взаимодействие

Если два или более магнита достаточно малы или достаточно удалены друг от друга, так что их форма и размер не имеют значения, то оба магнита можно смоделировать как магнитные диполи, имеющие магнитные моменты m ₁ и m ₂ . В случае однородно намагниченных сферических магнитов эта модель точна даже при конечном размере и расстоянии, поскольку внешнее поле таких магнитов представляет собой в точности дипольное поле.

Магнитное поле идеального диполя.

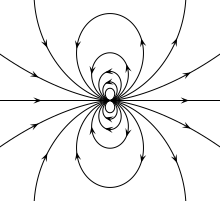
Магнитное поле магнитного диполя в векторных обозначениях равно: $$\mathbf {B} (\mathbf {m} ,\mathbf {r} )={\frac {\mu _{0}}{4\pi r^{3}}}\left(3(\mathbf {m} \cdot {\hat {\mathbf {r} }}){\hat {\mathbf {r} }}-\mathbf {m} \right)+{\frac {2\mu _{0}}{3}}\mathbf {m} \delta ^{3}(\mathbf {r} )$$ где

• B — поле
• r - вектор от положения диполя до места, где измеряется поле.
• r — абсолютное значение r : расстояние от диполя.
• ${\hat {\mathbf {r} }}=\mathbf {r} /r$ — единичный вектор, параллельный r ;
• m - (векторный) дипольный момент
• µ ₀ — проницаемость свободного пространства
• д ³ — трехмерная дельта-функция .

Это в точности поле точечного диполя, в точности дипольный член в мультипольном разложении произвольного поля и приблизительно поле любой дипольной конфигурации на больших расстояниях.

Системы отсчета для расчета сил между двумя диполями

Сила между магнитами коаксиального цилиндра. Согласно дипольному приближению, сила падает пропорционально $1/z^{4}$ для большого расстояния z , что приводит к наклону −4 на логарифмическом графике .

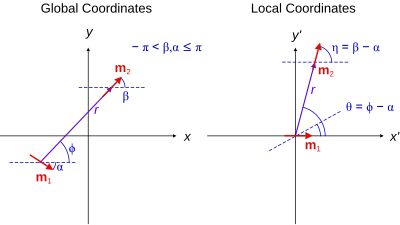
Если система координат сдвинута, чтобы центрировать ее на m ₁ , и повернута так, что ось x указывает в направлении m _1, то предыдущее уравнение упрощается до $${\begin{aligned}B_{x}(\mathbf {r} )&={\frac {\mu _{0}}{4\pi }}m_{1}\left({\frac {3\cos ^{2}\theta -1}{r^{3}}}\right)\\B_{y}(\mathbf {r} )&={\frac {\mu _{0}}{4\pi }}m_{1}\left({\frac {3\cos \theta \sin \theta }{r^{3}}}\right),\end{aligned}}$$ где переменные r и θ измеряются в системе отсчета с началом в m ₁ и ориентированы так, что m ₁ находится в начале координат, указывая в направлении x. Эта рамка называется Локальные координаты и показана на рисунке справа.

Сила одного магнитного диполя на другой определяется путем использования магнитного поля первого диполя, приведенного выше, и определения силы, возникающей из-за магнитного поля на втором диполе, с использованием приведенного выше уравнения силы. Используя векторные обозначения, сила магнитного диполя m ₁ на магнитном диполе m ₂ равна: $$\mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\frac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\frac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right]$$ где r — вектор расстояния от дипольного момента m ₁ до дипольного момента m ₂ , при этом r = ‖ r ‖ . Сила, действующая на m _1, направлена ​​в противоположном направлении. Например, магнитная сила для двух магнитов, направленных в направлении z, выровненных по оси z и разделенных расстоянием z, равна:

$\mathbf {F} (z,m_{1},m_{2})=-{\frac {3\mu _{0}m_{1}m_{2}}{2\pi z^{4}}}$, направление z.

Окончательные формулы показаны ниже. Они выражаются в глобальной системе координат, $${\begin{aligned}F_{r}(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\left[2\cos(\phi -\alpha )\cos(\phi -\beta )-\sin(\phi -\alpha )\sin(\phi -\beta )\right]\\F_{\phi }(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\sin(2\phi -\alpha -\beta )\end{aligned}}$$

См. также

• Магнитный двигатель