Ростки (игра)

Sprouts — это беспристрастная игра с карандашом и бумагой свойства которой можно проанализировать , математические . Его изобрели математики Джон Хортон Конвей и Майкл С. Патерсон. в Кембриджском университете в начале 1960-х годов. Настройка даже проще, чем у популярной игры с точками и коробочками , но игровой процесс развивается гораздо более художественно и органично.

Правила

Игра на 2 места в Sprouts. Игра заканчивается, когда первый игрок не может провести соединительную линию между двумя свободными точками, отмеченными зеленым.

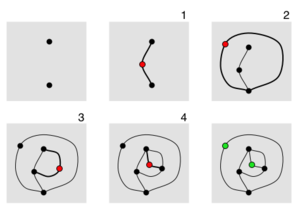
В игре участвуют два игрока, начиная с нескольких пятен, нарисованных на листе бумаги. Игроки ходят по очереди, причем каждый ход состоит из рисования линии между двумя точками (или от точки к себе) и добавления новой точки где-то вдоль линии. Игроки ограничены следующими правилами:

• Линия может быть прямой или изогнутой, но не должна касаться или пересекать себя или любую другую линию.
• Новое пятно не может быть размещено поверх одной из конечных точек новой линии. Таким образом, новое пятно делит линию на две более короткие линии.
• Ни к одному месту не может быть прикреплено более трех линий. Для целей этого правила линия от точки до самой себя считается двумя прикрепленными линиями, а новые точки считаются как имеющие две уже прикрепленные линии.
• Вы не можете дважды коснуться точки одной линией, а затем соединить ее с другой.

В так называемой нормальной игре побеждает игрок, сделавший последний ход. В мизер-игре проигрывает игрок, сделавший последний ход. Misère Sprouts — пожалуй, единственная комбинаторная игра Misère, в которую играют на организованном форуме состязательно.

На диаграмме справа показана игра Sprouts с двумя точками в обычной игре. После четвертого хода большинство точек мертвы – к ним прикреплены три линии, поэтому их нельзя использовать в качестве конечных точек для новой линии. Есть два пятна (показаны зеленым), которые все еще живы , и к ним прикреплено менее трех линий. Однако сделать еще один ход невозможно, потому что линия от живой точки к самой себе сделала бы четыре присоединения, а линия от одной живой точки к другой пересекла бы линии. Следовательно, пятый ход невозможен, и первый игрок проигрывает. Живые споты в конце игры называются выжившими и играют ключевую роль в анализе Ростков.

Количество ходов

Игра Ростки всегда завершается, хотя из правил игры этот факт не вытекает, поскольку количество клеток увеличивается с каждым ходом. Чтобы понять, почему игра всегда завершается, нужно учитывать количество жизней (возможностей соединить линию), а не количество мест. Тогда можно показать, что если игра начинается с n позиций, то она закончится не более чем за 3 n − 1 ходов и не менее чем за 2 n ходов.

В следующих доказательствах предполагается, что игра начинается с n позиций и длится ровно m ходов.

Максимальное количество ходов

Игра в ростки с n начальными точками (синим цветом), которая заканчивается за 3 n − 1 ходов.

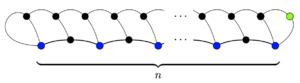
Каждая точка начинается с трех жизней , и каждый ход уменьшает общее количество жизней в игре на одну (на концах линии теряется две жизни, но в новой точке остается одна жизнь). Итак, в конце игры осталось 3 n − m жизней. В каждом выжившем месте есть только одна жизнь (иначе этот участок присоединился бы к себе еще одним ходом), поэтому выживших ровно 3 n − m . Должен остаться хотя бы один выживший, а именно место, добавленное последним ходом. Итак, 3 п - м ≥ 1 ; следовательно, игра может длиться не более 3 n − 1 ходов.

Эта верхняя граница на самом деле является максимальной, и ее можно достичь разными способами, гарантируя, что в конце игры останется только один выживший. Например, в игре справа один выживший и 3 n − 1 ходов.

Живые точки (зеленые) и их мертвые соседи (черные)

Минимальное количество ходов

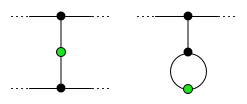
В конце игры мертвая точка называется соседом выжившего, если она либо примыкает к этому выжившему, либо, если у выжившего есть петля, она примыкает к месту, соседнему с выжившим. Это показано на диаграмме справа. У каждого выжившего есть ровно два мертвых соседа. Никакая мертвая точка не может быть соседом двух разных выживших, иначе выжившие могли бы объединиться. Все остальные мертвые точки (не соседи выжившего) называются фарисеями (от иврита « отделенные »). Предположим, есть p фарисеев. Затем

$n+m=3n-m+2(3n-m)+p$

поскольку начальные места + ходы = общее количество мест в конце игры = выжившие + соседи + фарисеи. Перестановка дает:

$m=2n+p/4$

Следовательно, игра длится не менее 2n ходов , а число фарисеев делится на 4.

Игра в ростки с n начальными позициями, заканчивающаяся за 2 n ходов.

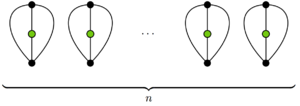
Эта нижняя граница продолжительности игры на самом деле является минимальной. На диаграмме справа показана завершенная игра из 2 n ходов. В нем n выживших, 2 n соседей и 0 фарисеев.

Важность в реальных играх

Реальные игры, похоже, превращаются в битву за то, будет ли количество ходов k или k + 1, при этом другие возможности маловероятны. Один игрок пытается создать закрытые регионы, содержащие выживших (таким образом уменьшая общее количество ходов, которые будут сыграны), а другой пытается создать фарисеев (таким образом увеличивая количество ходов, которые будут сыграны).

Выигрышные стратегии

Поскольку Sprouts — это конечная игра, в которой ничья невозможна, идеальная стратегия существует либо для первого, либо для второго игрока, в зависимости от количества начальных позиций. Главный вопрос относительно данной стартовой позиции заключается в том, чтобы определить, какой игрок сможет добиться победы, если будет играть идеально.

Когда выигрышная стратегия предназначена для первого игрока, говорят, что исход позиции является «выигрышем», а когда выигрышная стратегия предназначена для второго игрока, говорят, что исход позиции является «проигрышем». (потому что это проигрыш с точки зрения первого игрока).

Результат определяется путем построения дерева игры стартовой позиции. Это можно сделать вручную только для небольшого числа пятен, а все новые результаты с 1990 года были получены путем обширного поиска с помощью компьютеров.

Обычная версия

В журнале «Winning Ways for your Mathematical Plays» сообщается, что Денис Моллисон с помощью ручного анализа на 47 страницах доказал, что нормальная игра с 6 точками стала победой для второго игрока. Оно долгое время оставалось рекордом, вплоть до первого компьютерного анализа, который был проведен в Университете Карнеги-Меллона в 1990 году Дэвидом Эпплгейтом , Гаем Джейкобсоном и Дэниелом Слитером . Они заняли до 11 мест с одним из лучших аппаратных средств, доступных на тот момент.

Эпплгейт, Джейкобсон и Слитор заметили закономерность в своих результатах и ​​предположили , что у первого игрока есть выигрышная стратегия, когда количество мест, разделенное на шесть, оставляет остаток в три, четыре или пять. Это математический способ сказать, что закономерность, отображаемая в результате в таблице ниже, повторяется бесконечно, с периодом в шесть точек.

Пятна	0	1	2	3	4	5	6	7	8	9	10	11	...
Нормальный результат	Потеря	Потеря	Потеря	Победить	Победить	Победить	Потеря	Потеря	Потеря	Победить	Победить	Победить	...

В 2001 году Риккардо Фокарди и Фламина Луччио описали метод, позволяющий вручную доказать, что обычная игра с 7 точками является проигрышем.

Затем в 2006 году Джош Джордан расширил результаты вычислений до 14 точек. В 2007 году Жюльен Лемуан и Саймон Вьенно представили алгоритм, основанный на концепции нимберов , для ускорения вычислений, достигая 32 точек. Они увеличили количество мест до 44 в 2011 году и до трех изолированных стартовых позиций: 46, 47 и 53 места.

На данный момент все результаты нормальной игры согласуются с гипотезой Эпплгейта, Джейкобсона и Слиатора.

Версия страдания

История вычислений в «мизерной» версии Sprouts очень похожа на историю вычислений в обычной версии, в ней участвуют те же люди. Однако версию Misère вычислить труднее, и прогресс идет значительно медленнее.

В 1990 году Эпплгейт, Джейкобсон и Слитор поднялись до девяти позиций. Основываясь на своих результатах, они предположили, что результат соответствует регулярной схеме пятого периода. Однако эта гипотеза была признана недействительной в 2007 году, когда Джош Джордан и Роман Хорьков расширили анализ мизера до 12 позиций: игра с 12 мизерами является победой, а не предполагаемым поражением. В 2009 году эта же команда достигла 16 мест. В том же году Жюльен Лемуан и Симон Вьенно заняли 17 мест со сложными алгоритмами. В 2011 году им удалось расширить свой анализ до 20 пунктов.

Теперь предполагается, что результаты игры в мизер следуют схеме длиной шесть с некоторыми исключительными значениями: первый игрок выигрывает в игре Ростки мизер, когда остаток ( мод. 6) равен нулю, четырем или пяти, за исключением того, что первый игрок выигрывает один -очковую игру и проигрывает четырехочковую игру. В таблице ниже показана закономерность, два нестандартных значения выделены жирным шрифтом.

Пятна	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	...
Страдание	Победить	Победить	Потеря	Потеря	Потеря	Победить	Победить	Потеря	Потеря	Потеря	Победить	Победить	Победить	Потеря	Потеря	Потеря	...

Брюссельская капуста

Игра с двумя крестами в брюссельскую капусту всегда длится ровно восемь ходов.

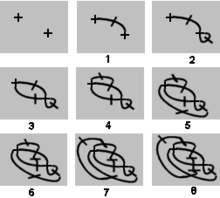
Вариант игры, названный «Брюссельская капуста» в честь крестоцветного овоща , начинается с нескольких крестиков, то есть пятен с четырьмя свободными концами. Каждое движение включает в себя соединение двух свободных концов кривой, опять же не пересекая существующие линии, а затем короткий штрих поперек линии, чтобы создать два новых свободных конца. Эта игра конечна, и общее количество ходов (и, следовательно, победитель игры) предопределено начальным количеством крестиков: игроки не могут повлиять на результат своей игрой. Таким образом, этот вариант можно назвать, в соответствии с категоризацией математики Конвеем, «игрой для одного игрока».

Каждое движение удаляет два свободных конца и вводит еще два. Тем не менее, игра обязательно закончится, поскольку некоторые свободные концы становятся изолированными. При n начальных крестиках число ходов, что примечательно, всегда будет равно 5 n − 2. Следовательно, игра, начинающаяся с нечетным числом крестов, будет победой первого игрока, а игра, начинающаяся с четного числа, будет победой второго игрока. игрок выигрывает независимо от ходов.

Чтобы доказать это, во-первых, мы утверждаем, что игра должна закончиться. Затем мы точно посчитаем, сколько ходов ему нужно, чтобы закончиться. Тогда подразумевается результат игры, как уже описано.

Рассматривайте каждый крест как граф с 5 вершинами и 4 ребрами. В исходной позиции с n крестами мы имеем плоский граф с v = 5 n вершинами, e = 4 n ребрами, f = 1 гранью и k = n компонентами связности . Эйлерова характеристика связных планарных графов равна 2. В несвязном планарном графе получаем

$1+k=f-e+v$

После m ходов имеем:

• e = 4 n + 4 m , так как за каждый ход игрок добавляет 4 ребра.
• v = 5 n + 3 m , так как за каждый ход игрок добавляет 3 вершины.

Тогда согласно вышесказанному мы имеем

• е - k знак равно 1 + е - v = 1 - п + м

Далее обратите внимание, что каждый раз, когда мы добавляем крест, мы гарантируем, что каждая сторона этого креста будет иметь вершину степени 1. Таким образом, на протяжении всей игры каждая грань имеет хотя бы одну вершину степени 1. Тем не менее, количество вершин степени 1 остается неизменным на протяжении всей игры и остается равным 4 n . Следовательно, f не превосходит 4 n .

Отсюда мы видим, что m = f − k − 1 + n не превышает 5 n − 2 (поскольку k не меньше 1, а f не превышает 4 n ). Таким образом, игра должна завершиться, и она должна завершиться не более чем за 5 n − 2 ходов. Теперь мы утверждаем, что он должен завершиться ровно за 5 n − 2 хода.

В окончательной конфигурации ни одна грань не может иметь более одной вершины степени 1, так как в противном случае мы могли бы соединить их крестом и все равно был бы допустимый ход. У каждой грани есть хотя бы одна такая вершина, поэтому она должна заканчиваться ровно одной такой вершиной. Итак, в окончательной конфигурации f равно ровно 4 n .

Аналогично, в окончательной конфигурации граф должен быть связным, поскольку внешняя грань получает хотя бы одну вершину степени 1 на каждую связную компоненту и не может иметь более одной такой вершины. Итак, в окончательной конфигурации k равно ровно 1.

Таким образом, для получения окончательной конфигурации мы должны были иметь m = f − k −1+ n = 4 n −1−1+ n = 5 n −2.

Также можно использовать комбинацию стандартной и брюссельской капусты. Игра начинается с произвольного количества ( n ) точек или крестиков. На каждом ходу игрок выбирает точку или крестик вдоль только что нарисованной линии. Продолжительность игры составляет от (2 n ) до ( 5 n − 2 ), в зависимости от количества добавленных точек или крестиков.

При n = 1, начиная с точки, игра закончится через 2 хода. Начиная с крестика, он закончится через 2 хода, если первый игрок добавит точку, и через 3 хода, если он добавит крестик: следовательно, у первого игрока есть выигрышная стратегия как для нормальной, так и для мизерной версии. При n > 1 анализ не завершается.

Ссылки

Библиография

• Элвин Р. Берлекамп , Джон Конвей и Ричард К. Гай , Пути победы в математических играх , 1992.
• Sprouts for Spring , Science News Online, заархивировано из оригинала 16 июля 2012 года .
• Причард, Д.Б. (1982). «Ростки». Мозговые игры . Пингвин Букс Лтд . стр. 169–71. ISBN  0-14-00-5682-3 .

Внешние ссылки

• Полный (?) список литературы по игре Ростки
• Ассоциация Всемирной игры ростков. , Дэнни Первис, ассоциация игроков Sprouts
• «Игра в ростки» в Университете Юты с интерактивным апплетом для игры между людьми. (Требуется Java)
• SproutsWiki , веб-сайт Жюльена Лемуана и Саймона Вьенно, с исходным кодом и двоичными файлами их программы.