Уравнение Ландау–Лифшица–Гильберта

В физике уравнение Ландау-Лифшица-Гилберта (обычно сокращенно уравнение ЛЛГ), названное в честь Льва Ландау , Евгения Лифшица и Т.Л. Гилберта , — это название, используемое для дифференциального уравнения, описывающего динамику (обычно прецессионное движение ) намагниченности $M.$ в твердом виде . Это модифицированная версия Гилберта исходного уравнения Ландау и Лифшица. ^{[ 1 ]} Уравнение ЛЛГ аналогично уравнению Блоха , но они отличаются формой затухающей части. Уравнение ЛЛГ описывает более общий сценарий динамики намагничивания, выходящий за рамки простой ларморовской прецессии . В частности, эффективное поле, вызывающее прецессионное движение $M,$ не ограничивается реальными магнитными полями; он включает в себя широкий спектр механизмов, включая магнитную анизотропию , обменное взаимодействие и так далее.

Различные формы уравнения ЛЛГ обычно используются в микромагнетике для моделирования эффектов магнитного поля и других магнитных взаимодействий на ферромагнитных материалах . Он обеспечивает практический способ моделирования поведения магнитных элементов во временной области. Недавние разработки обобщают уравнение ЛЛГ, включив в него влияние спин-поляризованных токов в виде крутящего момента, передающего спин . ^{[ 2 ]}

Уравнение Ландау–Лифшица

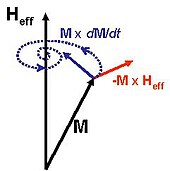
В ферромагнетике величина намагниченности M $в$ каждой точке пространства-времени аппроксимируется намагниченностью насыщения $M s$ (хотя она может быть меньше при усреднении по фрагменту объема). Уравнение Ландау-Лифшица, предшественник уравнения ЛЛГ, феноменологически описывает вращение намагниченности в ответ на эффективное поле $H eff,$ которое объясняет не только реальное магнитное поле, но и внутренние магнитные взаимодействия, такие как обмен и анизотропия. Более раннее, но эквивалентное уравнение (уравнение Ландау–Лифшица) было введено Ландау и Лифшицем (1935) : ^{[ 1 ]}

{\frac {\mathrm {d} \mathbf {M} }{\mathrm {d} t}}=-\gamma \mathbf {M} \times \mathbf {H_{\mathrm {eff} }} -\lambda \mathbf {M} \times \left(\mathbf {M} \times \mathbf {H_{\mathrm {eff} }} \right)

( 1 )

где $γ$ электрона — гиромагнитное отношение , а $λ$ — феноменологический параметр затухания, часто заменяемый на

\lambda =\alpha {\frac {\gamma }{M_{\mathrm {s} }}},

где $α$ — безразмерная константа, называемая коэффициентом затухания. Эффективное поле $H eff$ представляет собой комбинацию внешнего магнитного поля, размагничивающего поля и различных внутренних магнитных взаимодействий, включающих квантово-механические эффекты, которое обычно определяется как функциональная производная магнитной свободной энергии по отношению к локальной намагниченности $M$ . Чтобы решить это уравнение, необходимо включить дополнительные условия для размагничивающего поля, учитывающие геометрию материала.

Уравнение Ландау–Лифшица–Гильберта

В 1955 году Гилберт заменил затухающий член в уравнении Ландау–Лифшица (ЛЛ) на тот, который зависит от производной по времени намагниченности:

{\frac {\mathrm {d} \mathbf {M} }{\mathrm {d} t}}=-\gamma \left(\mathbf {M} \times \mathbf {H} _{\mathrm {eff} }-\eta \mathbf {M} \times {\frac {\mathrm {d} \mathbf {M} }{\mathrm {d} t}}\right)

( 2б )

Это уравнение Ландау–Лифшица–Гильберта (ЛЛГ), где $η$ — параметр затухания, характерный для материала. Его можно преобразовать в уравнение Ландау–Лифшица: ^{[ 3 ]}

{\frac {\mathrm {d} \mathbf {M} }{\mathrm {d} t}}=-\gamma '\mathbf {M} \times \mathbf {H} _{\mathrm {eff} }-\lambda \mathbf {M} \times (\mathbf {M} \times \mathbf {H} _{\mathrm {eff} })

( 2а )

где

\gamma '={\frac {\gamma }{1+\gamma ^{2}\eta ^{2}M_{s}^{2}}}\qquad {\text{and}}\qquad \lambda ={\frac {\gamma ^{2}\eta }{1+\gamma ^{2}\eta ^{2}M_{s}^{2}}}.

В этой форме уравнения ЛЛ член прецессии $γ'$ зависит от члена затухания. Это лучше отражает поведение реальных ферромагнетиков при большом затухании. ^{[ 4 ]}^{[ 5 ]}

Уравнение Ландау–Лифшица–Гильберта–Слончевского

В 1996 году Джон Слончевски расширил модель, чтобы учесть крутящий момент переноса спина , то есть крутящий момент, наведенный при намагничивании спин -поляризованным током, протекающим через ферромагнетик. Обычно это записывают в терминах единичного момента, $m = M / MS определяемого$ :

{\dot {\mathbf {m} }}=-\gamma \mathbf {m} \times \mathbf {H} _{\mathrm {eff} }+\alpha \mathbf {m} \times {\dot {\mathbf {m} }}+\tau _{\parallel }{\frac {\mathbf {m} \times (\mathbf {x} \times \mathbf {m} )}{\left|\mathbf {x} \times \mathbf {m} \right|}}+\tau _{\perp }{\frac {\mathbf {x} \times \mathbf {m} }{\left|\mathbf {x} \times \mathbf {m} \right|}}

где $\alpha$ – безразмерный параметр демпфирования, $\tau _{\perp }$ и $\tau _{\parallel }$ — движущие моменты, а $x$ — единичный вектор вдоль поляризации тока. ^{[ 6 ]}^{[ 7 ]}

Ссылки и сноски

^ Jump up to: ^а ^б Ландау Лев Давидович; Лифшич, Евгений М.; Питаевский Лев П.; Ландау, Лев Давидович (2006). Статистическая физика. 2: Теория конденсированного состояния / Е. М. Лифшица и Л. П. Питаевского . Курс теоретической физики / Л. Д. Ландау и Е. М. Лифшиц (Ред.). Оксфорд Берлингтон, Массачусетс: Эльзевир Баттерворт-Хайнеманн. ISBN 978-0-7506-2636-1 .
^ Ральф, округ Колумбия; Стайлз, доктор медицины (1 апреля 2008 г.). «Спиновые передаточные моменты» . Журнал магнетизма и магнитных материалов . 320 (7): 1190–1216. дои : 10.1016/j.jmmm.2007.12.019 . ISSN 0304-8853 .
^ Ахарони, Амикам (1996). Введение в теорию ферромагнетизма . Кларендон Пресс . ISBN 978-0-19-851791-7 .
^ Подробную информацию о нерезонансном эксперименте Келли и анализе Гилберта (который привел к изменению Гилбертом термина затухания) см. Gilbert, TL и Kelly, JM «Аномальное демпфирование вращения в ферромагнитных листах», Conf. Магнетизм и магнитные материалы, Питтсбург, Пенсильвания, 14–16 июня 1955 г. (Нью-Йорк: Американский институт инженеров-электриков, октябрь 1955 г., стр. 253–263 ). Текстовые ссылки на рисунки 5 и 6 должны были относиться к таблицам 1 и 2. Гилберт не мог соответствовать экспериментам Келли с фиксированным обычным гиромагнитным отношением $γ$ и частотно-зависимым $λ = αγ$ , но мог соответствовать этим данным для фиксированного гиромагнитного отношения Гилберта $γ G. = γ /(1+ α 2)$ и частотно-зависимое $α$ . Требовалось значение $α$ , равное 9, что указывает на очень широкое поглощение и, следовательно, на образец относительно низкого качества. Современные образцы при анализе по резонансному поглощению дают $значения α$ порядка 0,05 или меньше. Дж. Р. Мэйфилд, в J. Appl. Физ. Дополнение к Vol. 30, 256S-257S (1959), вверху слева на стр. 257S, пишет: «Как было впервые отмечено JC Slonczewski, наблюдаемый пик крутящего момента может быть интерпретирован с точки зрения эффектов вращательного переключения (резких переориентаций M), которые должны происходят, когда K/M ≤ H ≤ 2K/M». Поэтому интерпретация, данная Гилбертом, не была общепринятой.
^ Дж. Мэллинсон, «О затухающей гиромагнитной прецессии», в IEEE Transactions on Magnetics, vol. 23, нет. 4, стр. 2003–2004, июль 1987 г., номер документа: 10.1109/TMAG.1987.1065181.
^ Слончевски, Джон К. (1996). «Токовое возбуждение магнитных мультислоев». Журнал магнетизма и магнитных материалов . 159 (1): –1–L7. Бибкод : 1996JMMM..159L...1S . дои : 10.1016/0304-8853(96)00062-5 .
^ Вольф, Ю.А. (16 ноября 2001 г.). «Спинтроника: взгляд на спиновую электронику будущего» . Наука . 294 (5546): 1488–1495. Бибкод : 2001Sci...294.1488W . дои : 10.1126/science.1065389 . ПМИД 11711666 . S2CID 14010432 . Архивировано из оригинала 18 июня 2017 года.

Дальнейшее чтение

Гилберт, ТЛ (1955). «Лагранжева формулировка гиромагнитного уравнения магнитного поля». Физический обзор . 100 (4): 1243. Бибкод : 1955PhRv..100.1235. . дои : 10.1103/PhysRev.100.1235 . Это только абстрактно; полный отчет - «Проект Фонда исследований брони № A059, дополнительный отчет, 1 мая 1956 г.», но так и не был опубликован. Описание работы приведено в Гилберт, ТЛ (2004). «Феноменологическая теория затухания в ферромагнитных материалах». IEEE Транс. Магн . 40 (6): 3443–3449. Бибкод : 2004ITM....40.3443G . дои : 10.1109/TMAG.2004.836740 . S2CID 35628797 .
Ландау, LD ; Лифшиц, Э.М. (1935). «Теория дисперсии магнитной проницаемости в ферромагнитных телах». Физ. З. Советюнион . 8, 153.
Скроцкий, Г.В. (1984). «Возврат к уравнению Ландау – Лифшица». Сов. Физ. Усп . 27 (12): 977–979. Бибкод : 1984СвФУ..27..977С . дои : 10.1070/PU1984v027n12ABEH004101 .
Го, Болин; Дин, Шиджин (2008). Уравнения Ландау–Лифшица . Границы исследований с Китайской академией наук. Мировое научное издательство. ISBN 978-981-277-875-8 .
Цимрак, Иван (2007). «Обзор численных показателей и расчетов уравнения микромагнетизма Ландау – Лифшица» (PDF) . Архив вычислительных методов в технике . 15 (3): 1–37. дои : 10.1007/BF03024947 . S2CID 195272703 . Архивировано из оригинала (PDF) 5 июля 2015 г. Проверено 30 мая 2012 г.
М, Лакшманан (2010). «Увлекательный мир уравнения Ландау – Лифшица – Гилберта: обзор». Фил. Пер. Р. Сок. А. 369 (1939): 1280–1300. arXiv : 1101.1005 . Бибкод : 2011RSPTA.369.1280L . дои : 10.1098/rsta.2010.0319 . ПМИД 21320917 . S2CID 23275414 .

Внешние ссылки

Апплет динамики намагничивания

[:0-1] Jump up to: ^а ^б Ландау Лев Давидович; Лифшич, Евгений М.; Питаевский Лев П.; Ландау, Лев Давидович (2006). Статистическая физика. 2: Теория конденсированного состояния / Е. М. Лифшица и Л. П. Питаевского . Курс теоретической физики / Л. Д. Ландау и Е. М. Лифшиц (Ред.). Оксфорд Берлингтон, Массачусетс: Эльзевир Баттерворт-Хайнеманн. ISBN 978-0-7506-2636-1 .

[2] Ральф, округ Колумбия; Стайлз, доктор медицины (1 апреля 2008 г.). «Спиновые передаточные моменты» . Журнал магнетизма и магнитных материалов . 320 (7): 1190–1216. дои : 10.1016/j.jmmm.2007.12.019 . ISSN 0304-8853 .

[Aharoni96-3] Ахарони, Амикам (1996). Введение в теорию ферромагнетизма . Кларендон Пресс . ISBN 978-0-19-851791-7 .

[4] Подробную информацию о нерезонансном эксперименте Келли и анализе Гилберта (который привел к изменению Гилбертом термина затухания) см. Gilbert, TL и Kelly, JM «Аномальное демпфирование вращения в ферромагнитных листах», Conf. Магнетизм и магнитные материалы, Питтсбург, Пенсильвания, 14–16 июня 1955 г. (Нью-Йорк: Американский институт инженеров-электриков, октябрь 1955 г., стр. 253–263 ). Текстовые ссылки на рисунки 5 и 6 должны были относиться к таблицам 1 и 2. Гилберт не мог соответствовать экспериментам Келли с фиксированным обычным гиромагнитным отношением $γ$ и частотно-зависимым $λ = αγ$ , но мог соответствовать этим данным для фиксированного гиромагнитного отношения Гилберта $γ G. = γ /(1+ α 2)$ и частотно-зависимое $α$ . Требовалось значение $α$ , равное 9, что указывает на очень широкое поглощение и, следовательно, на образец относительно низкого качества. Современные образцы при анализе по резонансному поглощению дают $значения α$ порядка 0,05 или меньше. Дж. Р. Мэйфилд, в J. Appl. Физ. Дополнение к Vol. 30, 256S-257S (1959), вверху слева на стр. 257S, пишет: «Как было впервые отмечено JC Slonczewski, наблюдаемый пик крутящего момента может быть интерпретирован с точки зрения эффектов вращательного переключения (резких переориентаций M), которые должны происходят, когда K/M ≤ H ≤ 2K/M». Поэтому интерпретация, данная Гилбертом, не была общепринятой.

[5] Дж. Мэллинсон, «О затухающей гиромагнитной прецессии», в IEEE Transactions on Magnetics, vol. 23, нет. 4, стр. 2003–2004, июль 1987 г., номер документа: 10.1109/TMAG.1987.1065181.

[6] Слончевски, Джон К. (1996). «Токовое возбуждение магнитных мультислоев». Журнал магнетизма и магнитных материалов . 159 (1): –1–L7. Бибкод : 1996JMMM..159L...1S . дои : 10.1016/0304-8853(96)00062-5 .

[7] Вольф, Ю.А. (16 ноября 2001 г.). «Спинтроника: взгляд на спиновую электронику будущего» . Наука . 294 (5546): 1488–1495. Бибкод : 2001Sci...294.1488W . дои : 10.1126/science.1065389 . ПМИД 11711666 . S2CID 14010432 . Архивировано из оригинала 18 июня 2017 года.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]