Координаты Лоде

Поверхности, на которых инварианты $\xi$, $\rho$, $\theta$ постоянны. Построено в пространстве главных напряжений. Красная плоскость представляет собой меридиональную плоскость, а желтая плоскость — октаэдрическую плоскость.

Координаты Лоде $(z,r,\theta )$ или координаты Хейга – Вестергора $(\xi ,\rho ,\theta )$. представляют собой набор тензорных инвариантов , которые охватывают пространство действительных , симметричных , трехмерных тензоров второго порядка и изоморфны относительно пространства главных напряжений . Эта правосторонняя ортогональная система координат названа в честь немецкого ученого доктора Вальтера Лоде из-за его основополагающей статьи, написанной в 1926 году, описывающей влияние среднего главного напряжения на пластичность металла. Другими примерами наборов тензорных инвариантов являются набор главных напряжений. $(\sigma _{1},\sigma _{2},\sigma _{3})$ или набор кинематических инвариантов $(I_{1},J_{2},J_{3})$. Систему координат Лоде можно описать как цилиндрическую систему координат в пространстве главных напряжений с совпадающим началом координат и осью z, параллельной вектору. $(\sigma _{1},\sigma _{2},\sigma _{3})=(1,1,1)$.

Инварианты механики

Координаты Лоде проще всего вычислять с использованием инвариантов механики . Эти инварианты представляют собой смесь инвариантов тензора напряжений Коши , ${\boldsymbol {\sigma }}$, и девиатор напряжений , ${\boldsymbol {s}}$, и даны

$I_{1}=\mathrm {tr} ({\boldsymbol {\sigma }})$

$J_{2}={\frac {1}{2}}\left[{\text{tr}}({\boldsymbol {\sigma }}^{2})-{\frac {1}{3}}{\text{tr}}({\boldsymbol {\sigma }})^{2}\right]={\frac {1}{2}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)={\frac {1}{2}}\lVert {\boldsymbol {s}}\rVert ^{2}$

$J_{3}=\mathrm {det} ({\boldsymbol {s}})={\frac {1}{3}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)$

что можно эквивалентно записать в обозначениях Эйнштейна

$I_{1}=\sigma _{kk}$

$J_{2}={\frac {1}{2}}\left[{\text{tr}}({\boldsymbol {\sigma }}^{2})-{\frac {1}{3}}{\text{tr}}({\boldsymbol {\sigma }})^{2}\right]={\frac {1}{2}}s_{ij}s_{ji}={\frac {1}{2}}s_{ij}s_{ij}$

$J_{3}={\frac {1}{6}}\epsilon _{ijk}\epsilon _{pqr}\sigma _{ip}\sigma _{jq}\sigma _{kr}={\frac {1}{3}}s_{ij}s_{jk}s_{ki}$

где $\epsilon$ — это символ Леви-Чивита (или символ перестановки), а две последние формы — $J_{2}$ эквивалентны, потому что ${\boldsymbol {s}}$ симметричен ( $s_{ij}=s_{ji}$).

Градиенты этих инвариантов можно рассчитать по

${\frac {\partial I_{1}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {I}}$

${\frac {\partial J_{2}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {s}}={\boldsymbol {\sigma }}-{\frac {\mathrm {tr} \left({\boldsymbol {\sigma }}\right)}{3}}{\boldsymbol {I}}$

${\frac {\partial J_{3}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {T}}={\boldsymbol {s}}\cdot {\boldsymbol {s}}-{\frac {2J_{2}}{3}}{\boldsymbol {I}}$

где ${\boldsymbol {I}}$ - тождественный тензор второго порядка и ${\boldsymbol {T}}$ называется тензором Хилла.

Осевая координата $(z)$

The $z$-координата находится путем расчета величины ортогональной проекции напряженного состояния на гидростатическую ось.

$z={\boldsymbol {E_{z}}}\colon {\boldsymbol {\sigma }}={\frac {\mathrm {tr} ({\boldsymbol {\sigma }})}{\sqrt {3}}}={\frac {I_{1}}{\sqrt {3}}}$

где

${\boldsymbol {E_{z}}}={\frac {\boldsymbol {I}}{\lVert {\boldsymbol {I}}\rVert }}={\frac {\boldsymbol {I}}{\sqrt {3}}}$

– единица измерения нормали к гидростатической оси.

Радиальная координата $(r)$

The $r$-координата находится путем вычисления величины девиатора напряжений ( ортогональной проекции напряженного состояния на девиаторную плоскость).

$r={\boldsymbol {E_{r}}}\colon {\boldsymbol {\sigma }}=\lVert {\boldsymbol {s}}\rVert ={\sqrt {2J_{2}}}$

где

${\boldsymbol {E_{r}}}={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}$

showВывод

The relation that $r={\sqrt {2J_{2}}}$ can be found by expanding the relation $r={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}\colon {\boldsymbol {\sigma }}$ and writing $\sigma$ in terms of the isotropic and deviatoric parts while expanding the magnitude of ${\boldsymbol {s}}$ $r={\frac {\boldsymbol {s}}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}\colon \left({\boldsymbol {s}}+z{\boldsymbol {E_{z}}}\right)={\frac {1}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}\left({\boldsymbol {s}}\colon {\boldsymbol {s}}+z{\boldsymbol {s}}\colon {\boldsymbol {E_{z}}}\right)$. Because ${\boldsymbol {E_{z}}}$ is isotropic and ${\boldsymbol {s}}$ is deviatoric, their product is zero. Which leaves us with $r={\frac {{\boldsymbol {s}}\colon {\boldsymbol {s}}}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}={\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}$ Applying the identity ${\boldsymbol {A}}\colon {\boldsymbol {B}}=\mathrm {tr} \left({\boldsymbol {A}}^{T}\cdot {\boldsymbol {B}}\right)$ and using the definition of $J_{2}={\frac {1}{2}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)$ $r={\sqrt {\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)}}={\sqrt {2J_{2}}}$

— единичный тензор в направлении радиальной составляющей.

Угол Лоде – угловая координата $(\theta )$

Этот график показывает, что интуитивное приближение угла Лоде — это относительное положение среднего главного напряжения. $\lambda _{m}$ относительно малых и высоких главных напряжений.

Угол Лоде можно довольно условно рассматривать как меру типа нагрузки. Угол Лоде изменяется в зависимости от среднего собственного значения напряжения. Существует множество определений угла Лоде, каждое из которых использует разные тригонометрические функции: положительный синус, отрицательный синус, и положительный косинус (здесь обозначено $\theta _{s}$, ${\bar {\theta }}_{s}$, и $\theta _{c}$, соответственно)

$\sin(3\theta _{s})=-\sin(3{\bar {\theta }}_{s})=\cos(3\theta _{c})={\frac {J_{3}}{2}}\left({\frac {3}{J_{2}}}\right)^{3/2}$

и связаны

$\theta _{s}={\frac {\pi }{6}}-\theta _{c}\qquad \qquad \theta _{s}=-{\bar {\theta }}_{s}$

showВывод

The relation between $\theta _{c}$ and $\theta _{s}$ can be shown by applying a trigonometric identity relating sine and cosine by a shift $\cos(3\theta _{c})=\sin(3\theta _{s})$ $\cos(3\theta _{c})=\sin \left(\left(3\theta _{s}-{\frac {\pi }{2}}\right)+{\frac {\pi }{2}}\right)$ $\cos(3\theta _{c})=\cos \left(3\theta _{s}-{\frac {\pi }{2}}\right)$. Because cosine is an even function and the range of the inverse cosine is usually $0\leq \cos ^{-1}(\theta )\leq 1$ we take the negative possible value for the $\theta _{s}$ term, thus ensuring that $\theta _{c}$ is positive. $3\theta _{c}=\pm \left(3\theta _{s}-{\frac {\pi }{2}}\right)$ $\theta _{c}={\frac {\pi }{6}}-\theta _{s}$

Все эти определения определены для ряда $\pi /3$.

	Стрессовое состояние $\sigma _{1}\geq \sigma _{2}\geq \sigma _{3}$	$\theta _{s}$	${\bar {\theta }}_{s}$	$\theta _{c}$
диапазон		$-{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}$	$-{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}$	$0\leq \theta _{c}\leq {\frac {\pi }{3}}$
Трехосное сжатие (TXC)	$\sigma _{1}\geq \sigma _{2}=\sigma _{3}$	$-{\frac {\pi }{6}}$	${\frac {\pi }{6}}$	${\frac {\pi }{3}}$
Сдвиг (SHR)	$\sigma _{2}=(\sigma _{1}+\sigma _{3})/2$	$0$	$0$	${\frac {\pi }{6}}$
Трехосное расширение (TXE)	$\sigma _{1}=\sigma _{2}\geq \sigma _{3}$	${\frac {\pi }{6}}$	$-{\frac {\pi }{6}}$	$0$

Единичную нормаль в угловом направлении, завершающую ортонормированный базис, можно рассчитать для $\theta _{s}$ и $\theta _{c}$ с использованием

${\boldsymbol {E_{\theta s}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\sin(3\theta _{s}){\boldsymbol {E_{r}}}}{\cos(3\theta _{s})}}\qquad {\boldsymbol {E_{\theta c}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\cos(3\theta _{c}){\boldsymbol {E_{r}}}}{\sin(3\theta _{c})}}$.

Меридиональный профиль

На этом графике показан типичный меридиональный профиль нескольких моделей пластичности: фон Мизеса , линейной Друкера-Прагера , Мора-Кулона , Гурсона и Бигони-Пикколороаза . Верхняя часть графика отображает поведение поверхности текучести при трехосном растяжении, а нижняя часть изображает поведение поверхности текучести при трехосном сжатии.

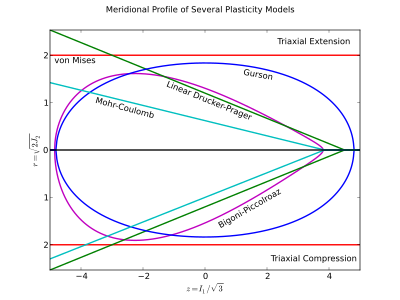
Меридиональный профиль представляет собой двухмерный график $(z,r)$ проведение $\theta$ постоянная и иногда отображается с использованием скалярных кратных $(z,r)$. Его обычно используют для демонстрации зависимости поверхности текучести от давления или траектории давления-сдвига траектории напряжения. Потому что $r$ неотрицательный , график обычно опускает отрицательную часть $r$-ось, но может быть включен для иллюстрации эффектов при противоположных углах Лоде (обычно трехосное растяжение и трехосное сжатие).

Одно из преимуществ построения меридионального профиля с помощью $(z,r)$ заключается в том, что это геометрически точное изображение поверхности текучести. Если для меридионального профиля используется неизоморфная пара, то нормаль к поверхности текучести не будет выглядеть нормальной в меридиональном профиле. Любая пара координат, отличающаяся от $(z,r)$ постоянными кратными одинакового абсолютного значения также изоморфны относительно пространства главных напряжений. Например, давление $p=-I1/3$ и напряжение фон Мизеса $\sigma _{v}={\sqrt {3J_{2}}}$ не являются изоморфной парой координат и, следовательно, искажают поверхность текучести, поскольку

$p=-{\frac {1}{\sqrt {3}}}z$

$\sigma _{v}={\sqrt {\frac {3}{2}}}r$

и, наконец, $|-1/{\sqrt {3}}|\neq |{\sqrt {3/2}}|$.

Октаэдрический профиль

На этом графике показан типичный октаэдрический профиль нескольких моделей пластичности: фон Мизеса , линейной Друкера–Прагера , Мора–Кулона , Гурсона и Бигони–Пикколоаза . На этом графике пропущены значения угла Лоде в пользу загрузки описаний из-за преобладания определений угла Лоде. Радиальная координата $r={\sqrt {2J_{2}}}$.

Октаэдрический профиль представляет собой двумерный график $(r,\theta )$ проведение $z$ постоянный. Построение поверхности текучести в октаэдрической плоскости демонстрирует уровень зависимости угла Лоде. Октаэдрическую плоскость иногда называют «плоскостью Пи». или «девиаторная плоскость».

Октаэдрический профиль не обязательно является постоянным для разных значений давления, за заметными исключениями критерия текучести фон Мизеса и критерия текучести Треска, которые постоянны для всех значений давления.

Примечание о терминологии

Термин «пространство Хайга-Вестергора» в литературе неоднозначно используется для обозначения как декартова пространства главных напряжений, так и пространства главных напряжений. и цилиндрическое координатное пространство Лоде

См. также

• Выход (инжиниринг)
• Пластичность (физика)
• Стресс
• Анри Треска
• стресс фон Мизеса
• Теория Мора – Кулона
• Напряжение
• Тензор деформации
• Тензор энергии-напряжения
• Концентрация стресса
• 3-D эластичность