Предпочтительный номер

В промышленном дизайне предпочтительные числа (также называемые предпочтительными значениями или предпочтительными сериями ) являются стандартными рекомендациями для выбора точных размеров продукта в рамках заданного набора ограничений. Разработчикам продукта приходится выбирать многочисленные длины, расстояния, диаметры, объемы и другие характерные величины . Хотя все эти варианты выбора ограничены соображениями функциональности, удобства использования, совместимости, безопасности или стоимости, обычно остается значительная свобода действий в выборе точного решения по многим параметрам.

Предпочтительные номера служат двум целям:

1. Их использование увеличивает вероятность совместимости объектов, созданных в разное время разными людьми. Другими словами, это одна из многих тактик стандартизации , будь то внутри компании или внутри отрасли, и она обычно желательна в промышленном контексте (если только целью не является привязка к поставщику или запланированное устаревание ).
2. Они выбираются таким образом, чтобы при производстве продукта разных размеров они располагались примерно на одинаковом расстоянии друг от друга в логарифмическом масштабе . Таким образом, они помогают свести к минимуму количество изделий различных размеров, которые необходимо производить или хранить на складе.

Предпочтительные числа представляют собой предпочтения простых чисел (таких как 1, 2 и 5), умноженных на степени удобного базиса, обычно 10.

Числа Ренарда

Основная статья: Серия Ренарда

В 1870 году Шарль Ренар предложил набор предпочтительных чисел. Его система была принята в 1952 году как международный стандарт ISO 3 . Система Ренара делит интервал от 1 до 10 на 5, 10, 20 или 40 шагов, что приводит к шкалам R5, R10, R20 и R40 соответственно. Множитель между двумя последовательными числами в ряду Ренара примерно постоянный (до округления), а именно корень 5-й, 10-й, 20-й или 40-й степени из 10 (приблизительно 1,58, 1,26, 1,12 и 1,06 соответственно), что приводит к геометрическому последовательность . Таким образом, максимальная относительная ошибка сводится к минимуму, если произвольное число заменяется ближайшим числом Ренара, умноженным на соответствующую степень 10. Пример: 1,0, 1,6, 2,5, 4,0, 6,3.

Серия Е

Основная статья: Серия E предпочтительных номеров

График двух декад номиналов резисторов серии E12, который дает значения резисторов от 1 до 82 Ом (Ом)

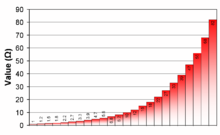
Серия E — еще одна система предпочтительных чисел. В его состав входят серии E1 , E3 , E6 , E12 , E24 , E48 , E96 и E192 . Основываясь на некоторых существующих производственных соглашениях, Международная электротехническая комиссия (МЭК) начала работу над новым международным стандартом в 1948 году. Первая версия этого стандарта IEC 63 (переименованная в IEC 60063 в 2007 году) была выпущена в 1952 году.

Он работает аналогично ряду Ренара, за исключением того, что интервал от 1 до 10 подразделяется на 3, 6, 12, 24, 48, 96 или 192 шага. Эти подразделения гарантируют, что при замене некоторого произвольного значения ближайшим предпочтительным числом максимальная относительная ошибка будет порядка 40%, 20%, 10%, 5% и т. д.

Использование серии E в основном ограничивается электронными деталями, такими как резисторы, конденсаторы, катушки индуктивности и стабилитроны. Обычно производимые размеры для других типов электрических компонентов либо выбираются из серии Renard, либо определяются в соответствующих стандартах на продукцию (например, провода ).

1–2–5 серии

В приложениях, для которых серия R5 обеспечивает слишком тонкую градацию, серия 1–2–5 иногда используется как более грубая альтернатива. Фактически это серия E3, округленная до одной значащей цифры:

… 0.1 0.2 0.5 1 2 5 10 20 50 100 200 500 1000 …

Эта серия охватывает десятилетие (соотношение 1:10) в три этапа. Соседние значения отличаются в 2 или 2,5 раза. В отличие от серии Ренара, серия 1–2–5 не была официально принята в качестве международного стандарта . Однако серию Renard R10 можно использовать для расширения серии 1–2–5 до более точной градации.

Эта серия используется для определения масштабов для графиков и для приборов, отображающих двухмерную форму с сеткой, таких как осциллографы .

Номиналы рядам большинства современных стерлингов , следуют валют, особенно евро и 1–2–5 . Соединенные Штаты и Канада следуют примерной серии 1–2–5: 1, 5, 10, 25, 50 (центов), 1 доллар, 2 доллара, 5 долларов, 10 долларов, 20 долларов, 50 долларов, 100 долларов. 1 ⁄ 4 – Серия 1 ⁄ 2 –1 (... 0,1 0,25 0,5 1 2,5 5 10 ...) также используется валютами, производными от бывшего голландского гульдена ( флорин Арубы , гульден Нидерландских Антильских островов , суринамский доллар ), некоторыми валютами Ближнего Востока ( иракский флорин , нидерландский антильский гульден, суринамский доллар). иорданские сейшельская динары, ливанский фунт , сирийский фунт ), а также рупия . Однако новые банкноты, выпущенные в Ливане и Сирии из-за инфляции, вместо этого следуют стандартным сериям 1–2–5.

Удобные номера

Основная статья: Удобные номера

В 1970-х годах Национальное бюро стандартов (NBS) определило набор удобных чисел для упрощения метрики в Соединенных Штатах . Эта система значений метрики описывалась как ряды 1–2–5 в обратном порядке, с отдачей предпочтения числам, кратным 5, 2 и 1 (плюс их степени 10), исключая линейные размеры выше 100 мм.

Звуковые частоты

ISO 266 «Акустика — Предпочтительные частоты» определяет две разные серии звуковых частот для использования в акустических измерениях. Обе серии относятся к стандартной опорной частоте 1000 Гц и используют серию Ренара R10 из ISO 3, причем одна использует степени 10, а другая связана с определением октавы как отношения частот 1:2.

Например, набор номинальных центральных частот для использования в аудиотестах и ​​аудиотестовом оборудовании:

Частоты, используемые в третьоктавных анализаторах слышимого диапазона

Номинальная центральная частота (Гц)
20
25
31.5
40
50
63
80
100
125
160
200
250
315
400
500
630
800
1000
1250
1600
2000
2500
3150
4000
5000
6300
8000
10000
12500
16000
20000

Компьютерная инженерия

При определении размеров компонентов компьютера в качестве предпочтительных чисел часто используются степени двойки:

 1    2    4    8   16   32   64  128  256  512  1024 ...

Если необходима более точная оценка, дополнительные предпочтительные числа получаются путем умножения степени двойки на небольшое нечетное целое число:

     1  2   4   8   16    32    64    128   256    512    1024 ...
(×3) 3  6   12  24  48    96    192   384   768    1536   3072 ...
(×5) 5  10  20  40  80    160   320   640   1280   2560   5120 ...
(×7) 7  14  28  56  112   224   448   896   1792   3584   7168 ...

Предпочтительные соотношения сторон

	16:	15:	12:
:8	2:1		3:2
:9	16:9	5:3	4:3
:10	8:5	3:2
:12	4:3	5:4	1:1

В компьютерной графике ширина и высота растровых изображений предпочтительно, чтобы были кратны 16, поскольку многие алгоритмы сжатия ( JPEG , MPEG ) делят цветные изображения на квадратные блоки такого размера. Черно-белые изображения JPEG разделены на блоки 8×8. Разрешение экрана часто соответствует тому же принципу. Здесь также важное влияние имеют предпочтительные соотношения сторон , например, 2:1, 3:2, 4:3, 5:3, 5:4, 8:5, 16:9.

Бумажные документы, конверты и ручки для рисования.

Основная статья: Размер бумаги

В стандартных метрических форматах бумаги используется квадратный корень из двух ( √ 2 ) как коэффициент между соседними размерами, округленный до ближайшего миллиметра ( Лихтенберга серия , ISO 216 ). Например, лист формата А4 имеет соотношение сторон очень близкое к √ 2 , а площадь очень близкую к 1/16 квадратного метра. A5 почти вполовину меньше A4 и имеет такое же соотношение сторон. Коэффициент √ 2 также появляется между стандартной толщиной пера для технических чертежей в ISO 9175-1: 0,13, 0,18, 0,25, 0,35, 0,50, 0,70, 1,00, 1,40 и 2,00 мм. Таким образом, можно получить перо нужного размера, чтобы продолжить рисунок, увеличенный до другого стандартного размера бумаги.

Фотография

В фотографии диафрагма, экспозиция и чувствительность пленки обычно подчиняются степеням 2:

Размер апертуры определяет, сколько света попадает в камеру. Измеряется в диафрагмах : f /1,4 , ж /2 , f /2,8 , f /4 и т. д. Полные значения диафрагмы представляют собой квадратный корень из двух . Настройки объектива камеры часто устанавливаются на промежутки в последовательные трети, поэтому каждая диафрагма представляет собой корень шестой степени из 2, округленный до двух значащих цифр: 1,0, 1,1, 1,2, 1,4, 1,6, 1,8, 2,0, 2,2, 2,5, 2,8. 3,2, 3,5, 4,0 и т. д. Расстояние называется «одна треть стопа». (Округление неточно в случаях f /1,2 , f /3,5 , f /5,6 , f /22 и т. д.)

Чувствительность пленки является мерой чувствительности пленки к свету. Это выражается в значениях ISO, например «ISO 100». В более раннем стандарте, который иногда все еще используется, используется термин «ASA», а не «ISO», имея в виду (бывшую) Американскую ассоциацию стандартов. Измеренная светочувствительность пленки округляется до ближайшего предпочтительного числа из модифицированной серии Renard, включая 100, 125, 160, 200, 250, 320, 400, 500, 640, 800... Это то же самое, что и округленная серия Renard R10 ' , за исключением использования 6,4 вместо 6,3 и более агрессивного округления ниже ISO 16. Однако в пленках, продаваемых любителям, используется ограниченная серия, включающая только степени, кратные двум ISO 100: 25, 50, 100, 200, 400. , 800, 1600 и 3200. Некоторые камеры бюджетного класса могут надежно считывать эти значения только с картриджей с пленкой с кодировкой DX, поскольку у них отсутствуют дополнительные электрические контакты, необходимые для считывания всей серии. Некоторые цифровые камеры расширяют этот двоичный ряд до таких значений, как 12800, 25600 и т. д. вместо модифицированных значений Ренарда 12500, 25000 и т. д.

Выдержка определяет , как долго объектив камеры будет открыт для приема света. Они выражаются в долях секунды, грубо, но не точно, на основе степеней 2: 1 секунда, 1 ⁄ 2 , 1 ⁄ 4 , 1 ⁄ 8 , 1 ⁄ 15 , 1 ⁄ 30 , 1 ⁄ 60 , 1 ⁄ 125 , 1 ⁄ 250 , 1 ⁄ 500 , 1/1000 ​ секунды .

Розничная упаковка

В некоторых странах законы о защите потребителей ограничивают количество различных размеров расфасованных продуктов, в которых могут продаваться определенные продукты, чтобы потребителям было легче сравнивать цены.

Примером такого регулирования является директива Европейского Союза об объёме некоторых расфасованных жидкостей (75/106/EEC). ). Он ограничивает список разрешенных размеров винных бутылок до 0,1, 0,25 ( 1 ⁄ 4 ), 0.375 ( 3 ⁄ 8 ), 0.5 ( 1 ⁄ 2 ), 0.75 ( 3 ⁄ 4 ), 1, 1,5, 2, 3 и 5 литров. Подобные списки существуют и для некоторых других видов продукции. Они различаются и часто значительно отклоняются от любого геометрического ряда, чтобы, когда это возможно, соответствовать традиционным размерам. Соседние размеры пакетов в этих списках обычно различаются по факторам. 2 ⁄ 3 или 3/4 даже , в некоторых случаях 1 ⁄ 2 , 4 ⁄ 5 или какое-либо другое соотношение двух маленьких целых чисел.

См. также

• Удобный номер
• Номинальное сопротивление
• Номинальный размер
• Предпочтительные метрические размеры

Дальнейшее чтение

• Хиршфельд, Кларенс Флойд ; Берри, Швейцария (4 декабря 1922 г.). «Стандартизация размеров по предпочтительным числам» . Машиностроение . 44 (12). Нью-Йорк, США: Американское общество инженеров-механиков : 791–. [1]
• Хейзелтин, Луи Алан (январь 1927 г.) [декабрь 1926 г.]. «Предпочтительные номера». Труды Института радиоинженеров . 14 (4). Институт радиоинженеров (ИРЭ): 785–787. дои : 10.1109/JRPROC.1926.221089 . ISSN   0731-5996 .
• Ван Дейк, Артур Ф. (февраль 1936 г.). «Предпочтительные номера». Труды Института радиоинженеров . 24 (2). Институт радиоинженеров (ИРЭ): 159–179. дои : 10.1109/JRPROC.1936.228053 . ISSN   0731-5996 . S2CID   140107818 . […] на выбор серии влияет тот факт, что эти единицы продаются с разными стандартными допусками, а именно пятью, десятью и двадцатью процентами, и есть желание, чтобы каждая изготовленная единица, независимо от того, какова может быть ее стоимость, падала в некоторый стандартный размер и допуск […]
• Баттнер, Гарольд Х.; Кольхаас, HT, ред. (1943). Справочные данные для радиоинженеров (1-е изд.). Федеральная телефонная и радиокорпорация (FTR). стр. 37–38 . Проверено 3 января 2020 г. (Примечание. В этой публикации 1943 года уже приведен список новых «предпочтительных значений сопротивления» после того, что было принято IEC для стандартизации с 1948 года и стандартизировано как серия E предпочтительных чисел в IEC 63:1952. Для сравнения в нем также перечислены «старые стандартные значения сопротивления» следующие: 50, 75, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 750, 1000 , 1200 , 1500 , 2000 , 2500 , 3000 , 3500 , 4 000 , 5000 , 7500 , 10 000 , 12 000 , 15 000 , 20 000 , 25 000 , 30 000 , 40 000 , 50 000 , 60 000 , 75 000 , 100 000 , 120 00 0 , 150 000 , 200 000 , 250 000 , 300 000 , 400 000 , 500 000 , 600 000 , 750 000 , 1 Мег, 1,5 Мег, 2,0 Мег, 3,0 Мег, 4,0 Мег, 5,0 Мег, 6,0 Мег, 7,0 Мег, 8,0 Мег, 9,0 Мэг, 10,0 0 Мэг.)
• Баттнер, Гарольд Х.; Кольхаас, ХТ; Манн, Ф.Дж., ред. (1946). Справочные данные для радиоинженеров (PDF) (2-е изд.). Федеральная телефонная и радиокорпорация (FTR). стр. 53–54. Архивировано (PDF) из оригинала 16 мая 2018 г. Проверено 3 января 2020 г. (Примечание. Показывает список «старых стандартных значений сопротивления» и новых «предпочтительных значений сопротивления» после более поздней стандартизированной серии предпочтительных чисел E. )
• Ван Дейк, Артур Ф. (март 1951 г.) [февраль 1951 г.]. «Предпочтительные номера». Труды Института радиоинженеров . 39 (2). Институт радиоинженеров (IRE): 115. doi : 10.1109/JRPROC.1951.230759 . ISSN   0096-8390 . […] Например, несколько лет назад Ассоциация производителей радио и телевидения сочла желательным стандартизировать номиналы резисторов. Был рассмотрен стандарт предпочтительных номеров ASA , но было сочтено, что он не соответствует условиям производства и практике покупки резисторов на данный момент, тогда как специальная серия номеров подходит лучше. Была принята специальная серия, и, поскольку это был официальный список RTMA, она использовалась более поздними комитетами RTMA для других применений, помимо резисторов, хотя изначально была принята из-за кажущихся преимуществ резисторов. По иронии судьбы, первоначальные преимущества в значительной степени исчезли из-за изменений в условиях производства резисторов. Но нестандартный стандарт остается… […]
• ISO 17:1973-04 – Руководство по использованию предпочтительных номеров и серий предпочтительных номеров . Международная организация по стандартизации (ISO). Апрель 1973 г. Архивировано из оригинала 2 ноября 2017 г. Проверено 2 ноября 2017 г. (Заменено: Рекомендация ISO R17-1956 — Предпочтительные номера — Руководство по использованию предпочтительных номеров и серий предпочтительных номеров . 1956 г. (1955 г.) и ISO R17/A1-1966 — Поправка 1 к Рекомендации ISO R17-1955 . 1966. )
• ISO 497:1973-05 – Руководство по выбору серий предпочтительных чисел и серий, содержащих более округленные значения предпочтительных чисел . Международная организация по стандартизации (ISO). Май 1973 г. Архивировано из оригинала 2 ноября 2017 г. Проверено 2 ноября 2017 г. (Заменено: Рекомендация ISO R497-1966 - Предпочтительные числа - Руководство по выбору серий предпочтительных чисел и серий, содержащих более округленные значения предпочтительных чисел . 1966. )
• ANSI Z17.1-1973 — Американский национальный стандарт предпочтительных номеров . Американский национальный институт стандартов (ANSI). 05.09.1973. (9 страниц) (Заменено: ASA Z17.1-1958 — Американский национальный стандарт предпочтительных номеров . 1958. Вновь подтвержден как USASI Z17.1-1958 в 1966 году и назван ANSI Z17.1-1958 с 1969 года.)
• Полин, Евгений (1 сентября 2007 г.). Логарифмы, стандартные числа, децибелы, Непер, Фон - конечно родственные! [ Логарифмы, предпочтительные числа, децибелы, непер, фон - естественно связаны! ] (PDF) (на немецком языке). Архивировано (PDF) из оригинала 18 декабря 2016 г. Проверено 18 декабря 2016 г.
• Кинцле, Отто Хельмут [на немецком языке] (04 октября 2013 г.) [1950]. Написано в Ганновере, Германия. Номера стандартизации [ предпочтительные номера ]. Научная стандартизация (на немецком языке). Том 2 (перепечатка 1-го изд.). Берлин / Геттинген / Гейдельберг, Германия: Springer-Verlag OHG . ISBN  978-3-642-99831-7 . Проверено 1 ноября 2017 г. (340 страниц)
• Бергтольд, Фриц (1965). Математика для радиоэлектронщиков [ Математика для радиоэлектронщиков ] (на немецком языке) (3-е изд.). Мюнхен, Германия: Францис-Верлаг .
• Бауэр, Хорст, изд. Автомобильная промышленность в мягкой обложке (на немецком языке) (22-е изд.). Дюссельдорф, Германия: Bosch , VDI-Verlag . ISBN  3-18419122-2 .
• Рис, Клеменс (1962). Стандартизация ( по предпочтительным числам на немецком языке) (1-е изд.). Берлин, Германия: Duncker & Humblot Verlag . ISBN  3-42801242-9 . (135 страниц)
• Берг, Зигфрид (1949). номер Прикладной предпочтительный - Сборник статей ] (на немецком языке). Берлин/Кёльн, Германия: Beuth-Vertrieb GmbH . Проверено 1 ноября 2017 г. (191 страница)
• Таффентсаммер, Карл; Шумахер, П. (1953). «Предпочтительные числа — таблица однозначных логарифмов инженера». Мастерская технологии и машиностроения (на немецком языке). 43 (4): 156.
• Таффензаммер, Карл (1956). «Децилог, мост между логарифмами, децибелами, неперами и предпочтительными числами». Журнал VDI (на немецком языке). 98 :267-274.
• Штрарингер, Вильгельм (1952). ( на Волшебный мир предпочтительных чисел немецком языке). Франкфурт а. Майн, Германия: Verlags- und Wirtschaftsgesellschaft der Elektrowerke mbH (VWEW). (95 страниц)