Гидравлическая головка

Жидкость течет из бака вверху в бассейн внизу под давлением гидронапора.

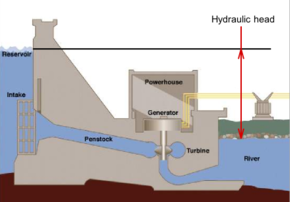
Гидравлический напор или пьезометрический напор — это конкретное измерение давления жидкости над вертикальной точкой отсчета . ^[1]^[2]

Обычно его измеряют как высоту поверхности жидкости, выраженную в единицах длины, на входе (или дне) пьезометра . В водоносном горизонте его можно рассчитать по глубине до воды в пьезометрической скважине (специализированной водяной скважине ) и учитывая информацию о высоте пьезометра и глубине экрана. Гидравлический напор можно аналогичным образом измерить в столбе воды с помощью пьезометра на стояке путем измерения высоты поверхности воды в трубке относительно общей точки отсчета. Гидравлическая головка может использоваться для определения гидравлического градиента между двумя или более точками.

Определение

В гидродинамике напор — это понятие, которое связывает энергию жидкости несжимаемой с высотой эквивалентного статического столба этой жидкости. Согласно принципу Бернулли , полная энергия в данной точке жидкости представляет собой кинетическую энергию, связанную со скоростью потока жидкости, плюс энергию статического давления в жидкости, плюс энергию высоты жидкости относительно произвольной точки отсчета. . ^[3] Голова выражается в единицах расстояния, таких как метры или футы. Сила, действующая на единицу объема жидкости в гравитационном поле, равна ρg, где ρ — плотность жидкости, а g — ускорение свободного падения . На Земле дополнительная высота пресной воды добавляет статическое давление примерно 9,8 кПа на метр (0,098 бар / м) или 0,433 фунта на квадратный дюйм на фут высоты водного столба.

Статический напор насоса — это максимальная высота (давление), которую он может обеспечить. Производительность насоса при определенной частоте вращения можно определить по его кривой QH (расход в зависимости от высоты).

Напор полезен при определении центробежных насосов , поскольку их характеристики перекачки обычно не зависят от плотности жидкости.

Обычно существует четыре типа голов:

Скорость напора обусловлена объемным движением ( кинетической энергией ) жидкости. $h_{v}={\tfrac {1}{2}}\rho v^{2}/\rho g={\frac {1}{2}}{\frac {v^{2}}{g}}$ Обратите внимание, что $\rho gh_{v}$ равно динамическому давлению для безвихревого течения .
Подъем напора обусловлен весом жидкости, силой гравитации, действующей на столб жидкости. Высота подъема — это просто высота ( h ) жидкости над произвольно обозначенной нулевой точкой: $h_{e}=\rho gh/\rho g$
Напор возникает из-за статического давления — внутреннего молекулярного движения жидкости, которое оказывает силу на контейнер. Оно равно давлению, разделенному на силу/объем жидкости в гравитационном поле: $h_{p}=p/\rho g$
Напор сопротивления (или напор трения , или потеря напора ) возникает из-за сил трения, действующих против движения жидкости в контейнере. Для сплошной среды это описывается законом Дарси , который связывает объемный расход ( q ) с градиентом гидравлического напора через гидравлическую проводимость K : $\mathbf {q} =-K\nabla h$ в то время как в трубопроводной системе потери напора описываются уравнением Хагена – Пуазейля и уравнением Бернулли .

Компоненты

После свободного падения с высоты $h$ в вакууме от начальной скорости 0 масса достигнет скорости $v={\sqrt {{2g}{h}}}$ где $g$ это ускорение свободного падения. Переставлено как голова : $h={\frac {v^{2}}{2g}}.$

Термин ${\frac {v^{2}}{2g}}$ называется скоростным напором и выражается как измерение длины. В текущей жидкости он представляет собой энергию жидкости, обусловленную ее объемным движением.

Общий гидравлический напор жидкости состоит из напора напора и напора подъема . ^[1]^[2] Напор — это эквивалентное манометрическое давление столба воды у основания пьезометра, а напор — это относительная потенциальная энергия, выраженная в единицах высоты. Уравнение напора , упрощенная форма принципа Бернулли для несжимаемых жидкостей, может быть выражено как: $h=\psi +z$ где

$h$ — это гидравлический напор ( длина в м или футах), также известный как пьезометрический напор.
$\psi$ - напор , выраженный в перепаде высот водяного столба относительно дна пьезометра ( длина в м или футах), и
$z$ - высота нижней части пьезометра ( длина в м или футах)

В примере с пьезометром глубиной 400 м, высотой 1000 м и глубиной до воды 100 м: z = 600 м, ψ = 300 м и h = 900 м.

Напор можно выразить как: $\psi ={\frac {P}{\gamma }}={\frac {P}{\rho g}}$ где $P$ - манометрическое давление (сила на единицу площади, часто Па или фунт на квадратный дюйм),

$\gamma$ — единица веса жидкости (сила на единицу объема, обычно Н·м). ⁻³ или фунт-сила /фут ³),
$\rho$ плотность м жидкости (масса на единицу объема, часто кг· ⁻³), и
$g$ — ускорение свободного падения (изменение скорости в единицу времени, часто м·с ⁻²)

Напор пресной воды

Напор зависит от плотности воды, которая может меняться в зависимости как от температуры, так и от химического состава ( в частности, солености ). Это означает, что расчет гидравлического напора зависит от плотности воды внутри пьезометра. Если необходимо сравнить одно или несколько измерений гидравлического напора, их необходимо стандартизировать, обычно по напору пресной воды , который можно рассчитать как:

h_{\mathrm {fw} }=\psi {\frac {\rho }{\rho _{\mathrm {fw} }}}+z

где

$h_{\mathrm {fw} }$ - напор пресной воды (длина, измеренная в м или футах), и
$\rho _{\mathrm {fw} }$ плотность . пресной воды (масса на единицу объема, обычно в кг·м) ⁻³)

Гидравлический градиент

Гидравлический градиент представляет собой векторный градиент между двумя или более измерениями гидравлического напора по длине пути потока. Для грунтовых вод его также называют уклоном Дарси , поскольку он определяет величину потока или расхода Дарси . Он также имеет применение в потоке в открытом канале , где он также известен как градиент потока и может использоваться для определения того, набирает или теряет энергию участок. гидравлический градиент Безразмерный можно рассчитать между двумя точками с известными значениями напора как: $i={\frac {dh}{dl}}={\frac {h_{2}-h_{1}}{\mathrm {length} }}$ где

$i$ – гидравлический градиент (безразмерный),
$dh$ это разница между двумя гидравлическими напорами (длина, обычно в метрах или футах), и
$dl$ длина пути потока между двумя пьезометрами (длина, обычно в м или футах)

Гидравлический градиент можно выразить в векторной записи, используя del оператор . гидравлического напора Для этого требуется поле , которое практически можно получить только из численных моделей, таких как MODFLOW для грунтовых вод или стандартного шага или HEC-RAS для открытых каналов. В декартовых координатах это можно выразить так: $\nabla h=\left({\frac {\partial h}{\partial x}},{\frac {\partial h}{\partial y}},{\frac {\partial h}{\partial z}}\right)={\frac {\partial h}{\partial x}}\mathbf {i} +{\frac {\partial h}{\partial y}}\mathbf {j} +{\frac {\partial h}{\partial z}}\mathbf {k}$ Этот вектор описывает направление потока грунтовых вод, где отрицательные значения указывают на поток по измерению, а ноль указывает на отсутствие потока. Как и в любом другом примере в физике, энергия должна течь сверху вниз, поэтому поток имеет отрицательный градиент. Этот вектор можно использовать в сочетании с законом Дарси и тензором гидравлической проводимости для определения потока воды в трех измерениях.

В грунтовых водах

Связь между напорами для *гидростатического* случая и *случая нисходящего потока* .

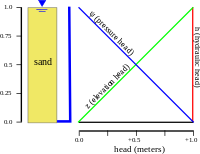
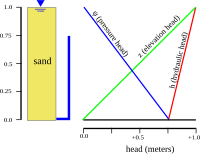
Распределение гидравлического напора через водоносный горизонт определяет, куда будут течь грунтовые воды. В гидростатическом примере (первый рисунок), где гидравлический напор постоянный, поток отсутствует. Однако если существует разница в гидравлическом напоре сверху вниз из-за слива снизу (второй рисунок), вода будет течь вниз из-за разницы в напоре, также называемой гидравлическим градиентом .

Атмосферное давление

Несмотря на то, что при расчете гидравлического напора принято использовать манометрическое давление , правильнее использовать абсолютное давление (манометрическое давление + атмосферное давление ), поскольку оно действительно является движущей силой потока грунтовых вод. Часто подробные наблюдения за барометрическим давлением не доступны для каждой скважины во времени, поэтому этим часто пренебрегают (что способствует большим ошибкам в местах, где гидравлические градиенты низкие или угол между скважинами острый).

Влияние изменений атмосферного давления на уровень воды, наблюдаемое в скважинах, известно уже много лет. Эффект прямой, повышение атмосферного давления – это увеличение нагрузки на воду в водоносном горизонте, что увеличивает глубину до воды (понижает высоту уровня воды). Паскаль впервые качественно наблюдал эти эффекты в 17 веке, а более строго они были описаны почвенным физиком Эдгаром Бэкингемом (работающим в Министерстве сельского хозяйства США (USDA)) с использованием моделей воздушного потока в 1907 году.

Потеря головы

В любой реальной движущейся жидкости энергия рассеивается из-за трения ; турбулентность рассеивает еще больше энергии для потоков с большим числом Рейнольдса . Это рассеяние, называемое потерей напора , делится на две основные категории: «большие потери», связанные с потерями энергии на длину трубы, и «незначительные потери», связанные с изгибами, фитингами, клапанами и т. д. Наиболее распространенное уравнение, используемое для расчета основных потерь. потери напора представляют собой уравнение Дарси – Вейсбаха . Более старыми, более эмпирическими подходами являются уравнение Хазена-Вильямса и уравнение Прони .

Для относительно коротких трубопроводных систем с относительно большим количеством изгибов и фитингов незначительные потери могут легко превысить крупные потери. При проектировании незначительные потери обычно оцениваются по таблицам с использованием коэффициентов или более простого и менее точного приведения малых потерь к эквивалентной длине трубы - метод, часто используемый для сокращенных расчетов падения давления в линиях пневмотранспорта. ^[4]

См. также

Примечания

^ Jump up to: ^а ^б Малли, Раймонд (2004), Поток промышленных жидкостей: теория и уравнения , CRC Press, ISBN 978-0849327674 , 410 стр. См. стр. 43–44.
^ Jump up to: ^а ^б Шансон, Хьюберт (2004), Гидравлика потока в открытом канале: Введение , Баттерворт – Хайнеманн, ISBN 978-0750659789 , 650 страниц. См. стр. 22.
^ Стритер, Виктор Л. (1958) Механика жидкости , раздел 3.7 (четвертое издание) McGraw-Hill
^ «Эквивалентная длина трубы (Пневматическая транспортировка)» .

Ссылки

Беар, Дж. 1972. Динамика жидкостей в пористых средах , Дувр. ISBN 0-486-65675-6 .
другие ссылки, в которых обсуждается гидравлический напор в контексте гидрогеологии, см. в разделе «Дальнейшая литература» на этой странице.

[Mulley_43_44-1] Jump up to: ^а ^б Малли, Раймонд (2004), Поток промышленных жидкостей: теория и уравнения , CRC Press, ISBN 978-0849327674 , 410 стр. См. стр. 43–44.

[Chanson_22-2] Jump up to: ^а ^б Шансон, Хьюберт (2004), Гидравлика потока в открытом канале: Введение , Баттерворт – Хайнеманн, ISBN 978-0750659789 , 650 страниц. См. стр. 22.

[3] Стритер, Виктор Л. (1958) Механика жидкости , раздел 3.7 (четвертое издание) McGraw-Hill

[4] «Эквивалентная длина трубы (Пневматическая транспортировка)» .

[1]

[2]

[3]

[4]

v т и Гидроэнергетика
гидроэлектроэнергии Производство	Плотина Список обычных гидроэлектростанций Гидроаккумулирующая гидроэлектроэнергия Малая гидроэлектростанция Микро ГЭС Пико гидро Русловая гидроэлектростанция
Гидроэнергетическое оборудование	Турбина Фрэнсиса турбина Каплана Тайсон турбина Винтовая турбина Горлова Колесо Пелтона Турго турбины Поперечная турбина Водяное колесо