Побитовая операция

В компьютерном программировании побитовая операция выполняется над битовой строкой , битовым массивом или двоичным числом (рассматриваемым как битовая строка) на уровне отдельных битов . Это быстрое и простое действие, лежащее в основе арифметических операций более высокого уровня и напрямую поддерживаемое процессором . Большинство побитовых операций представлены в виде инструкций с двумя операндами, результат которых заменяет один из входных операндов.

На простых недорогих процессорах побитовые операции обычно выполняются существенно быстрее, чем деление, в несколько раз быстрее, чем умножение, а иногда и значительно быстрее, чем сложение. Хотя современные процессоры обычно выполняют сложение и умножение так же быстро, как и побитовые операции, из-за более длинных конвейеров команд и других вариантов архитектуры , побитовые операции обычно потребляют меньше энергии из-за меньшего использования ресурсов. ^[1]

Побитовые операторы

В пояснениях ниже любые указания на положение бита отсчитываются с правой (наименее значимой) стороны, продвигаясь влево. Например, двоичное значение 0001 (десятичное 1) имеет нули в каждой позиции, кроме первой (т. е. самой правой).

НЕТ

Побитовое НЕ или побитовое дополнение — это унарная операция , которая выполняет логическое отрицание каждого бита, образуя дополнение до единиц данного двоичного значения. Биты, равные 0, становятся 1, а биты, равные 1, становятся 0. Например:

NOT 0111  (decimal 7)
  = 1000  (decimal 8)

NOT 10101011  (decimal 171)
  = 01010100  (decimal 84)

Результат равен дополнению двух значений минус один. Если используется арифметика с дополнением до двух, то NOT x = -x − 1.

Для целых чисел без знака побитовое дополнение числа представляет собой «зеркальное отражение» числа через половину диапазона целого числа без знака. Например, для 8-битных целых чисел без знака: NOT x = 255 - x, который можно визуализировать на графике в виде нисходящей линии, которая эффективно «переворачивает» возрастающий диапазон от 0 до 255 на уменьшающийся диапазон от 255 до 0. Простой, но наглядный пример использования — инвертировать изображение в оттенках серого, где каждый пиксель хранится как целое число без знака.

И

Побитовое И — это двоичная операция , которая принимает два двоичных представления одинаковой длины и выполняет логическую операцию И над каждой парой соответствующих битов. Таким образом, если оба бита в сравниваемой позиции равны 1, бит в результирующем двоичном представлении равен 1 (1 × 1 = 1); в противном случае результатом будет 0 (1 × 0 = 0 и 0 × 0 = 0). Например:

    0101 (decimal 5)
AND 0011 (decimal 3)
  = 0001 (decimal 1)

ли конкретный бит Эту операцию можно использовать для определения того, установлен (1) или очищен (0). Например, учитывая битовый шаблон 0011 (десятичное 3), чтобы определить, установлен ли второй бит, мы используем побитовое И с битовым шаблоном, содержащим 1 только во втором бите:

    0011 (decimal 3)
AND 0010 (decimal 2)
  = 0010 (decimal 2)

Поскольку результат 0010 не равен нулю, мы знаем, что второй бит в исходном шаблоне был установлен. Это часто называют битовой маскировкой . (По аналогии, использование малярной ленты закрывает или маскирует части, которые не следует изменять, или части, которые не представляют интереса. В этом случае значения 0 маскируют биты, которые не представляют интереса.)

Побитовое И может использоваться для очистки выбранных битов (или флагов ) регистра, в котором каждый бит представляет отдельное логическое состояние . Этот метод является эффективным способом хранения ряда логических значений, используя как можно меньше памяти.

Например, 0110 (десятичное 6) можно рассматривать как набор из четырех флагов, пронумерованных справа налево, где первый и четвертый флаги сброшены (0), а второй и третий флаги установлены (1). Третий флаг можно очистить с помощью поразрядного И с шаблоном, в котором ноль есть только в третьем бите:

    0110 (decimal 6)
AND 1011 (decimal 11)
  = 0010 (decimal 2)

Благодаря этому свойству становится легко проверить четность двоичного числа, проверив значение младшего бита. Используя приведенный выше пример:

    0110 (decimal 6)
AND 0001 (decimal 1)
  = 0000 (decimal 0)

Поскольку 6 И 1 равно нулю, 6 делится на два и, следовательно, четно.

ИЛИ

Побитовое ИЛИ — это двоичная операция , которая принимает два битовых шаблона одинаковой длины и выполняет логическую инклюзивную операцию ИЛИ над каждой парой соответствующих битов. Результат в каждой позиции равен 0, если оба бита равны 0, а в противном случае результат равен 1. Например:

   0101 (decimal 5)
OR 0011 (decimal 3)
 = 0111 (decimal 7)

Побитовое ИЛИ может использоваться для установки в 1 выбранных битов регистра, описанного выше. Например, четвертый бит 0010 (десятичное 2) может быть установлен путем выполнения побитового ИЛИ с шаблоном, в котором установлен только четвертый бит:

   0010 (decimal 2)
OR 1000 (decimal 8)
 = 1010 (decimal 10)

БЕСПЛАТНО

Побитовое исключающее ИЛИ — это двоичная операция , которая принимает два битовых шаблона одинаковой длины и выполняет логическую операцию исключающего ИЛИ для каждой пары соответствующих битов. Результат в каждой позиции равен 1, если только один из битов равен 1, но будет равен 0, если оба равны 0 или оба равны 1. При этом мы выполняем сравнение двух битов, получая 1, если два бита различны, и 0. если они одинаковы. Например:

    0101 (decimal 5)
XOR 0011 (decimal 3)
  = 0110 (decimal 6)

Побитовое исключающее ИЛИ может использоваться для инвертирования выбранных битов в регистре (также называемое переключением или переключением). Любой бит можно переключить с помощью операции XOR с 1. Например, учитывая битовый шаблон 0010 (десятичное 2), второй и четвертый биты могут быть переключены с помощью побитового исключающего ИЛИ с битовым шаблоном, содержащим 1 во второй и четвертой позициях:

    0010 (decimal 2)
XOR 1010 (decimal 10)
  = 1000 (decimal 8)

Этот метод можно использовать для управления битовыми шаблонами, представляющими наборы логических состояний.

Программисты на языке ассемблера и оптимизирующие компиляторы иногда используют XOR как ярлык для установки значения регистра в ноль. Выполнение XOR над значением против самого себя всегда дает ноль, и во многих архитектурах эта операция требует меньше тактов и меньше памяти, чем загрузка нулевого значения и сохранение его в регистр.

Если набор битовых строк фиксированной длины n (т. е. машинные слова ) рассматривается как n -мерное векторное пространство ${\bf {F}}_{2}^{n}$ над полем ${\bf {F}}_{2}$ , то сложение векторов соответствует побитовому исключающему ИЛИ.

Математические эквиваленты

Предполагая ⁠ $x\geq y$ ⁠ для неотрицательных целых чисел побитовые операции можно записать следующим образом:

{\begin{aligned}\operatorname {NOT} x&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+1\right){\bmod {2}}\right]=2^{\left\lfloor \log _{2}(x)\right\rfloor +1}-1-x\\x\operatorname {AND} y&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\\x\operatorname {OR} y&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)-\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right)\\x\operatorname {XOR} y&=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left(\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right]{\bmod {2}}\right)=\sum _{n=0}^{\lfloor \log _{2}(x)\rfloor }2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor +\left\lfloor {\frac {y}{2^{n}}}\right\rfloor \right){\bmod {2}}\right]\end{aligned}}

Таблица истинности для всех бинарных логических операторов

Существует 16 возможных функций истинности двух двоичных переменных ; это определяет таблицу истинности .

Вот побитовые эквивалентные операции двух битов P и Q:

Побитовый эквиваленты		0	НЕТ (п ИЛИ q)	(НЕ п) И q	НЕТ п	р И (НЕ q)	НЕТ д	п исключающее ИЛИ q	НЕТ (p И q)	р И q	НЕТ (p исключающее ИЛИ q)	д	(НЕ п) ИЛИ q	п	п ИЛИ (НЕ q)	п ИЛИ q	1
п	д	Ф ⁰	НИ ¹	Xq ²	¬p ³	↛ ⁴	¬q ⁵	БЕСПЛАТНО ⁶	NAND ⁷	И ⁸	ИСНО-ИЛИ ⁹	д ¹⁰	Если/то ¹¹	п ¹²	Тогда/если ¹³	ИЛИ ¹⁴	Т ¹⁵
1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
1	0	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
0	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
0	0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Битовые сдвиги

Битовые сдвиги иногда считаются побитовыми операциями, поскольку они рассматривают значение как последовательность битов, а не как числовую величину. В этих операциях цифры перемещаются или смещаются влево или вправо. Регистры в компьютерном процессоре имеют фиксированную ширину, поэтому некоторые биты будут «сдвинуты» из регистра на одном конце, в то время как такое же количество бит «сдвинуто» с другого конца; различия между операторами сдвига битов заключаются в том, как они определяют значения сдвинутых битов.

Битовая адресация

Если ширина регистра (часто 32 или даже 64) больше количества битов (обычно 8) наименьшей адресуемой единицы, часто называемой байтом, операции сдвига вызывают схему адресации от байтов к битам. Таким образом, ориентации «влево» и «вправо» берутся из стандартного написания чисел в разрядной записи , так что сдвиг влево увеличивает, а сдвиг вправо уменьшает значение числа – если сначала читаются левые цифры, это составляет ориентацию с прямым порядком байтов . Не принимая во внимание граничные эффекты на обоих концах регистра, арифметические и логические операции сдвига ведут себя одинаково, а сдвиг на 8-битные позиции переносит битовую комбинацию на 1-байтовую позицию следующим образом:

Прямой порядок:	сдвиг влево на 8 позиций увеличивает адрес байта на 1,
	сдвиг вправо на 8 позиций уменьшает адрес байта на 1.
Порядок с прямым порядком байтов :	сдвиг влево на 8 позиций уменьшает адрес байта на 1,
	сдвиг вправо на 8 позиций увеличивает адрес байта на 1.

Арифметический сдвиг

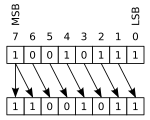
При арифметическом сдвиге биты, сдвинутые с любого конца, отбрасываются. При арифметическом сдвиге влево нули сдвигаются вправо; при арифметическом сдвиге вправо знаковый бит (старший бит в дополнении до двух) сдвигается влево, таким образом сохраняя знак операнда.

В этом примере используется 8-битный регистр, интерпретируемый как дополнение до двух:

   00010111 (decimal +23) LEFT-SHIFT
=  00101110 (decimal +46)

   10010111 (decimal −105) RIGHT-SHIFT
=  11001011 (decimal −53)

В первом случае самая левая цифра была сдвинута за конец регистра, а новый 0 был сдвинут в самую правую позицию. Во втором случае крайняя правая 1 была сдвинута (возможно, во флаг переноса ), а новая 1 скопирована в крайнюю левую позицию, сохраняя знак числа. Несколько смен иногда сокращаются до одной смены на некоторое количество цифр. Например:

   00010111 (decimal +23) LEFT-SHIFT-BY-TWO
=  01011100 (decimal +92)

Арифметический сдвиг влево на n эквивалентен умножению на 2. ^н (при условии, что значение не переполняется ), а арифметический сдвиг вправо на n значения дополнения до двух эквивалентен взятию нижнего предела деления на 2 ^н. Если двоичное число рассматривается как дополнение до единиц , то та же операция сдвига вправо приводит к делению на 2. ^н и округление к нулю .

Логический сдвиг

При логическом сдвиге нули сдвигаются, чтобы заменить отброшенные биты. Следовательно, логический и арифметический сдвиг влево совершенно одинаковы.

Однако, поскольку логический сдвиг вправо вставляет 0 битов в самый старший бит вместо копирования знакового бита, он идеально подходит для беззнаковых двоичных чисел, в то время как арифметический сдвиг вправо идеально подходит для со знаком , дополненных до двух двоичных чисел .

Круговой сдвиг

Другой формой сдвига является круговой сдвиг , побитовое вращение или побитовое вращение .

Поворот

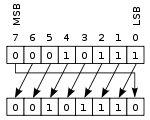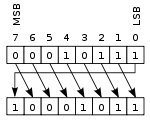В этой операции, иногда называемой ротацией без переноса , биты «вращаются», как если бы левый и правый концы регистра были соединены. Значение, которое смещается вправо во время сдвига влево, — это любое значение, которое было сдвинуто влево, и наоборот для операции сдвига вправо. Это полезно, если необходимо сохранить все существующие биты, и часто используется в цифровой криптографии . ^{[ нужны разъяснения ]}

Поворот через перенос

Поворот посредством переноса — это вариант операции поворота, при котором сдвигаемый бит (на любом конце) представляет собой старое значение флага переноса, а сдвигаемый бит (на другом конце) становится новым значением флага переноса. флаг переноса.

Один поворот посредством переноса может имитировать логический или арифметический сдвиг на одну позицию, предварительно установив флаг переноса. Например, если флаг переноса содержит 0, то x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE является логическим сдвигом вправо, и если флаг переноса содержит копию знакового бита, то x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE представляет собой арифметический сдвиг вправо. По этой причине некоторые микроконтроллеры, такие как PIC нижнего уровня, просто выполняют вращение и вращение посредством переноса и не беспокоятся об арифметических или логических инструкциях сдвига.

процессора Ротация через перенос особенно полезна при выполнении сдвигов чисел, превышающих собственный размер слова , поскольку, если большое число хранится в двух регистрах, бит, сдвинутый с одного конца первого регистра, должен войти в другой конец. второй. При ротационном переносе этот бит «сохраняется» во флаге переноса во время первой смены и готов к смещению во время второй смены без какой-либо дополнительной подготовки.

На языках высокого уровня

В семье языков C

В языках C и C++ операторами логического сдвига являются: <<"для левого смещения и" >>" для сдвига вправо. Число позиций для сдвига задается в качестве второго аргумента оператора. Например,

x = y << 2;

назначает x результат сдвига y влево на два бита, что эквивалентно умножению на четыре.

Сдвиги могут привести к поведению, определяемому реализацией, или к неопределенному поведению , поэтому при их использовании необходимо соблюдать осторожность. Результатом сдвига на количество битов, большее или равное размеру слова, является неопределенное поведение в C и C++. ^[2]^[3] Сдвиг вправо отрицательного значения определяется реализацией и не рекомендуется хорошей практикой кодирования; ^[4] результат сдвига влево знакового значения не определен, если результат не может быть представлен в типе результата. ^[2]

В C# сдвиг вправо — это арифметический сдвиг, когда первый операнд имеет значение int или long. Если первый операнд имеет тип uint или ulong, сдвиг вправо является логическим сдвигом. ^[5]

Круговые сдвиги

В языках семейства C отсутствует оператор поворота (хотя C++20 предоставляет std::rotl и std::rotr), но его можно синтезировать из операторов сдвига. Необходимо позаботиться о том, чтобы оператор был правильно сформирован, чтобы избежать на неопределенное поведение и атак время в программном обеспечении с требованиями безопасности. ^[6] Например, простая реализация, которая поворачивает влево 32-битное беззнаковое значение. x к n позиции - это просто

uint32_t x = ..., n = ...;
uint32_t y = (x << n) | (x >> (32 - n));

Однако сдвиг на 0 бит приводит к неопределенному поведению в правом выражении (x >> (32 - n)) потому что 32 - 0 является 32, и 32 находится за пределами диапазона 0–31 включительно. Вторая попытка может привести к

uint32_t x = ..., n = ...;
uint32_t y = n ? (x << n) | (x >> (32 - n)) : x;

где величина сдвига проверяется, чтобы убедиться, что она не приводит к неопределенному поведению. Однако эта ветвь добавляет дополнительный путь кода и предоставляет возможность временного анализа и атаки, что часто неприемлемо в программном обеспечении с высокой степенью целостности. ^[6] Кроме того, код компилируется в несколько машинных инструкций, что часто менее эффективно, чем собственные инструкции процессора.

Чтобы избежать неопределенного поведения и ветвей в GCC и Clang , рекомендуется следующее. Шаблон распознается многими компиляторами, и компилятор выдает одну команду поворота: ^[7]^[8]^[9]

uint32_t x = ..., n = ...;
uint32_t y = (x << n) | (x >> (-n & 31));

Существуют также встроенные функции , специфичные для компилятора, реализующие циклические сдвиги , такие как _rotl8, _rotl16 , _rotr8, _rotr16 в Microsoft Visual C++ . Clang предоставляет некоторые встроенные функции ротации для совместимости с Microsoft, которые страдают от описанных выше проблем. ^[9] GCC не предлагает встроенные функции вращения. Intel также предоставляет встроенные функции x86 .

Ява

В Java все целочисленные типы подписаны, поэтому " <<" и " >>"Операторы выполняют арифметические сдвиги. Java добавляет оператор " >>>" для выполнения логических сдвигов вправо, но поскольку логические и арифметические операции сдвига влево идентичны для целых чисел со знаком, " <<<"Оператор в Java.

Более подробная информация об операторах сдвига Java: ^[10]

Операторы << (левая смена), >> (подписанный правый сдвиг) и >>> (беззнаковый сдвиг вправо) называются операторами сдвига .
Тип выражения сдвига — это расширенный тип левого операнда. Например, aByte >>> 2 эквивалентно ((int) aByte) >>> 2.
Если расширенный тип левого операнда — int, в качестве расстояния сдвига используются только пять младших битов правого операнда. Это как если бы правый операнд был подвергнут побитовому логическому оператору И & со значением маски 0x1f (0b11111). ^[11] Таким образом, фактически используемый диапазон переключения всегда находится в диапазоне от 0 до 31 включительно.
Если расширенный тип левого операнда длинный, то в качестве расстояния сдвига используются только шесть младших битов правого операнда. Это как если бы правый операнд был подвергнут побитовому логическому оператору И & со значением маски 0x3f (0b111111). ^[11] Таким образом, фактически используемый диапазон переключения всегда находится в диапазоне от 0 до 63 включительно.
Стоимость n >>> s — это n позиций, сдвинутых вправо, битовых с нулевым расширением.
В битовых операциях и операциях сдвига тип byte неявно преобразуется в int. Если значение байта отрицательное, старший бит равен единице, тогда единицы используются для заполнения дополнительных байтов в int. Так byte b1 = -5; int i = b1 | 0x0200; приведет к i == -5.

JavaScript

JavaScript использует побитовые операции для оценки каждой из двух или более единиц места в 1 или 0. ^[12]

Паскаль

В Паскале, а также во всех его диалектах (таких как Object Pascal и Standard Pascal ), логическими операторами сдвига влево и вправо являются « shl" и " shr" соответственно. Даже для целых чисел со знаком shr ведет себя как логический сдвиг и не копирует знаковый бит. В качестве второго аргумента указывается количество мест для сдвига. Например, следующая команда присваивает x результат сдвига y влево на два бита:

x := y shl 2;

Другой

popcount , используемый в криптографии
считать ведущие нули

Приложения

Побитовые операции особенно необходимы в программировании нижнего уровня, таком как драйверы устройств, низкоуровневая графика, сборка пакетов протоколов связи и декодирование.

Хотя машины часто имеют эффективные встроенные инструкции для выполнения арифметических и логических операций, все эти операции могут быть выполнены путем комбинирования побитовых операторов и проверки нуля различными способами. ^[13] Например, вот псевдокода реализация древнеегипетского умножения, показывающая, как умножать два произвольных целых числа. a и b ( a больше, чем b), используя только битовые сдвиги и сложение:

c ← 0
while b ≠ 0
    if (b and 1) ≠ 0
        c ← c + a
    left shift a by 1
    right shift b by 1
return c

Другой пример — реализация сложения в псевдокоде, показывающая, как вычислить сумму двух целых чисел. a и b использование побитовых операторов и нулевого тестирования:

while a ≠ 0
    c ← b and a
    b ← b xor a
    left shift c by 1
    a ← c
return b

Булева алгебра

Иногда полезно упростить сложные выражения, состоящие из побитовых операций, например при написании компиляторов. Цель компилятора — преобразовать язык программирования высокого уровня в максимально эффективный машинный код . Булева алгебра используется для упрощения сложных поразрядных выражений.

И

x & y = y & x
x & (y & z) = (x & y) & z
x & 0xFFFF = x^[14]
x & 0 = 0

x & x = x

ИЛИ

x | y = y | x
x | (y | z) = (x | y) | z
x | 0 = x
x | 0xFFFF = 0xFFFF
x | x = x

НЕТ

~(~x) = x

БЕСПЛАТНО

x ^ y = y ^ x
x ^ (y ^ z) = (x ^ y) ^ z
x ^ 0 = x
x ^ y ^ y = x
x ^ x = 0
x ^ 0xFFFF = ~x

Кроме того, XOR может быть составлен с использованием трех основных операций (И, ИЛИ, НЕ).

a ^ b = (a | b) & (~a | ~b)
a ^ b = (a & ~b) | (~a & b)

Другие

x | (x & y) = x
x & (x | y) = x
~(x | y) = ~x & ~y
~(x & y) = ~x | ~y
x | (y & z) = (x | y) & (x | z)
x & (y | z) = (x & y) | (x & z)
x & (y ^ z) = (x & y) ^ (x & z)
x + y = (x ^ y) + ((x & y) << 1)
x - y = ~(~x + y)

Обратные и решение уравнений

Решить переменные в булевой алгебре может быть сложно, потому что в отличие от обычной алгебры некоторые операции не имеют обратных. При выполнении операций без обратных операций некоторые исходные биты данных теряются, и эту недостающую информацию невозможно восстановить.

Имеет инверсный
- НЕТ
- БЕСПЛАТНО
- Повернуть влево
- Повернуть вправо
Не повернуть вспять
- И
- ИЛИ
- Сдвиг влево
- Сдвиг вправо

Порядок действий

Операции, находящиеся вверху этого списка, выполняются первыми. Более полный список смотрите в основной статье.

( )
~ -^[15]
* / %
+ -^[16]
<< >>
&
^
|

См. также

Ссылки

^ «Блог CMicrotek по маломощному дизайну» . CМикротек . Проверено 12 августа 2015 г.
^ Перейти обратно: ^а ^б JTC1/SC22/WG14 N843 «Язык программирования C» , раздел 6.5.7
^ «Арифметические операторы — cppreference.com» . ru.cppreference.com . Проверено 6 июля 2016 г.
^ «INT13-C. Используйте побитовые операторы только с беззнаковыми операндами» . CERT: Стандарты безопасного кодирования . Институт программной инженерии Университета Карнеги-Меллона . Проверено 7 сентября 2015 г.
^ «Оператор (Справочник по C#)» . Майкрософт . Проверено 14 июля 2013 г.
^ Перейти обратно: ^а ^б «Почти постоянное вращение по времени, не нарушающее стандарты?» . Сеть обмена стеками . Проверено 12 августа 2015 г.
^ «Плохая оптимизация идиомы портативного вращения» . Проект GNU GCC . Проверено 11 августа 2015 г.
^ «Круговое вращение, не нарушающее стандарт C/C++?» . Форумы разработчиков Intel . Проверено 12 августа 2015 г.
^ Перейти обратно: ^а ^б «Константа не передается во встроенную сборку, что приводит к тому, что «ограничение 'I' ожидает целочисленное константное выражение»» . Проект ЛЛВМ . Проверено 11 августа 2015 г.
^ Спецификация языка Java, раздел 15.19. Операторы смены
^ Перейти обратно: ^а ^б «Глава 15. Выражения» . oracle.com .
^ «Побитовый JavaScript» . W3Schools.com .
^ «Синтез арифметических операций с использованием трюков со сдвигом битов» . Bisqwit.iki.fi. 15 февраля 2014 г. Проверено 8 марта 2014 г.
^ В этой статье 0xFFFF означает, что все биты вашего типа данных должны быть установлены в 1. Точное количество бит зависит от ширины типа данных.
^ - здесь отрицание, а не вычитание
^ - здесь вычитание, а не отрицание

Внешние ссылки

Онлайн-побитовый калькулятор поддерживает побитовое И, ИЛИ и XOR.
XORcat , инструмент для побитового XOR файлов/потоков.
Деление с использованием битовых сдвигов
« Побитовые операции Mod N », Энрике Зелени, Демонстрационный проект Wolfram .
« Сюжеты композиций побитовых операций », Энрике Зелени, Демонстрационный проект Wolfram.

[1] «Блог CMicrotek по маломощному дизайну» . CМикротек . Проверено 12 августа 2015 г.

[:0-2] Перейти обратно: ^а ^б JTC1/SC22/WG14 N843 «Язык программирования C» , раздел 6.5.7

[3] «Арифметические операторы — cppreference.com» . ru.cppreference.com . Проверено 6 июля 2016 г.

[4] «INT13-C. Используйте побитовые операторы только с беззнаковыми операндами» . CERT: Стандарты безопасного кодирования . Институт программной инженерии Университета Карнеги-Меллона . Проверено 7 сентября 2015 г.

[5] «Оператор (Справочник по C#)» . Майкрософт . Проверено 14 июля 2013 г.

[StackOverflow-6] Перейти обратно: ^а ^б «Почти постоянное вращение по времени, не нарушающее стандарты?» . Сеть обмена стеками . Проверено 12 августа 2015 г.

[7] «Плохая оптимизация идиомы портативного вращения» . Проект GNU GCC . Проверено 11 августа 2015 г.

[8] «Круговое вращение, не нарушающее стандарт C/C++?» . Форумы разработчиков Intel . Проверено 12 августа 2015 г.

[LLVM-9] Перейти обратно: ^а ^б «Константа не передается во встроенную сборку, что приводит к тому, что «ограничение 'I' ожидает целочисленное константное выражение»» . Проект ЛЛВМ . Проверено 11 августа 2015 г.

[10] Спецификация языка Java, раздел 15.19. Операторы смены

[jls15.22.1-11] Перейти обратно: ^а ^б «Глава 15. Выражения» . oracle.com .

[12] «Побитовый JavaScript» . W3Schools.com .

[13] «Синтез арифметических операций с использованием трюков со сдвигом битов» . Bisqwit.iki.fi. 15 февраля 2014 г. Проверено 8 марта 2014 г.

[:1-14] В этой статье 0xFFFF означает, что все биты вашего типа данных должны быть установлены в 1. Точное количество бит зависит от ширины типа данных.

[15] - здесь отрицание, а не вычитание

[16] - здесь вычитание, а не отрицание

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]