✖


Jump to content

Код исправления ошибок

(Перенаправлено из Кодирование канала )
«Перемежитель» перенаправляется сюда. Чтобы узнать о волоконно-оптическом устройстве, см. оптический перемежитель .

В вычислительной технике , телекоммуникациях , теории информации и теории кодирования используется прямое исправление ошибок ( FEC ) или канальное кодирование. [1] [2] [3] метод, используемый для контроля ошибок при передаче данных по ненадежным или зашумленным каналам связи .

Основная идея заключается в том, что отправитель кодирует сообщение избыточным способом, чаще всего с помощью кода исправления ошибок или кода исправления ошибок ( ECC ). [4] [5] Избыточность позволяет получателю не только обнаруживать ошибки , которые могут возникнуть в любом месте сообщения, но часто исправлять ограниченное количество ошибок. Поэтому обратный канал для запроса повторной передачи может не потребоваться. Цена — фиксированная, более высокая пропускная способность прямого канала.

Американский математик Ричард Хэмминг был пионером в этой области в 1940-х годах и в 1950 году изобрел первый код исправления ошибок: код Хэмминга (7,4) . [5]

FEC может применяться в ситуациях, когда повторная передача является дорогостоящей или невозможной, например, в односторонних каналах связи или при многоадресной передаче нескольким получателям .

Соединения с большой задержкой также выигрывают; в случае спутников, вращающихся вокруг далеких планет, повторная передача из-за ошибок приведет к задержке в несколько часов. FEC также широко используется в модемах и сотовых сетях .

Обработка FEC в приемнике может применяться к цифровому потоку битов или к демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью первоначального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала, искаженного шумом. Многие декодеры FEC также могут генерировать сигнал частоты ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.

Информация FEC добавляется к устройствам хранения данных (магнитным, оптическим и твердотельным/флэш-памятям), чтобы обеспечить восстановление поврежденных данных, и используется в качестве ECC компьютерной памяти в системах, которые требуют специальных мер для обеспечения надежности.

Максимальная доля ошибок или пропущенных битов, которые можно исправить, определяется конструкцией ECC, поэтому для разных условий подходят разные коды прямого исправления ошибок. В общем, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных и одновременно улучшает полученное эффективное соотношение сигнал/шум . Теорема о кодировании канала с шумом Клода Шеннона может использоваться для расчета максимально достижимой полосы пропускания связи при заданной максимально приемлемой вероятности ошибки. Это устанавливает границы теоретической максимальной скорости передачи информации для канала с некоторым заданным базовым уровнем шума. Однако доказательство не является конструктивным и, следовательно, не дает понимания того, как создать код достижения пропускной способности. После многих лет исследований некоторые передовые системы FEC, такие как полярный код, [3] приближаются к теоретическому максимуму, определяемому пропускной способностью канала Шеннона в рамках гипотезы о кадре бесконечной длины.

Метод [ править ]

ECC достигается путем добавления избыточности к передаваемой информации с использованием алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появиться или не появиться в закодированном выводе буквально; Коды, включающие неизмененные входные данные в выходные, являются систематическими , а те, которые этого не делают, — несистематическими .

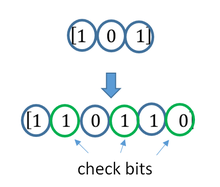
Упрощенный пример ECC — передача каждого бита данных 3 раза, что известно как код повторения (3,1) . Через канал с шумом приемник может увидеть 8 версий выходного сигнала, см. таблицу ниже.

Тройка получена Интерпретируется как
000 0 (без ошибок)
001 0
010 0
100 0
111 1 (без ошибок)
110 1
101 1
011 1

Это позволяет исправить ошибку в любом из трех образцов путем «голосования большинства» или «демократического голосования». Корректирующая способность этого ECC:

  • Ошибка до 1 бита триплета или
  • до 2 битов триплета опущено (случаи не показаны в таблице).

Несмотря на простоту реализации и широкое использование, такое тройное модульное резервирование является относительно неэффективным ECC. Лучшие коды ECC обычно проверяют последние несколько десятков или даже последние несколько сотен ранее полученных битов, чтобы определить, как декодировать текущую небольшую горстку битов (обычно в группах от 2 до 8 бит).

Усреднение шума для уменьшения ошибок [ править ]

Можно сказать, что ECC работает путем «усреднения шума»; поскольку каждый бит данных влияет на множество передаваемых символов, искажение некоторых символов шумом обычно позволяет извлечь исходные пользовательские данные из других, неповрежденных полученных символов, которые также зависят от тех же пользовательских данных.

  • Из-за этого эффекта «объединения рисков» цифровые системы связи, использующие ECC, имеют тенденцию работать значительно выше определенного минимального отношения сигнал/шум , а не ниже него.
  • Эта тенденция «все или ничего» — эффект обрыва — становится более выраженной по мере использования более сильных кодов, которые более близко приближаются к теоретическому пределу Шеннона .
  • Перемежение кодированных данных ECC может уменьшить свойства «все или ничего» передаваемых кодов ECC, когда ошибки канала имеют тенденцию возникать пакетами. Однако этот метод имеет ограничения; его лучше всего использовать для узкополосных данных.

Большинство телекоммуникационных систем используют фиксированный канальный код, в наихудшем случае предназначенный для того, чтобы выдерживать ожидаемую частоту ошибок по битам , а затем вообще перестают работать, если частота ошибок по битам становится еще хуже. Однако некоторые системы адаптируются к данным условиям ошибок канала: некоторые экземпляры гибридного автоматического запроса повторения используют фиксированный метод ECC, пока ECC может обрабатывать частоту ошибок, а затем переключаются на ARQ , когда частота ошибок становится слишком высокой; адаптивная модуляция и кодирование использует различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокая частота ошибок, или удаляя их, когда они не нужны.

Типы [ править ]

Основные статьи: Блочный код и сверточный код
Блочный код (в частности, код Хэмминга ), в котором избыточные биты добавляются в виде блока в конец исходного сообщения.
Непрерывный сверточный код , в котором избыточные биты непрерывно добавляются в структуру кодового слова.

Двумя основными категориями кодов ECC являются блочные коды и сверточные коды .

  • Блочные коды работают с блоками (пакетами) битов или символов фиксированного размера. Практические блочные коды обычно могут быть жестко декодированы за полиномиальное время относительно длины их блока.
  • Сверточные коды работают с потоками битов или символов произвольной длины. Чаще всего они мягко декодируются с помощью алгоритма Витерби , хотя иногда используются и другие алгоритмы. Декодирование Витерби обеспечивает асимптотически оптимальную эффективность декодирования с увеличением длины ограничения сверточного кода, но за счет экспоненциального увеличения сложности. Сверточный код, который завершается, также является «блочным кодом», поскольку он кодирует блок входных данных, но размер блока сверточного кода обычно произволен, тогда как блочные коды имеют фиксированный размер, определяемый их алгебраическими характеристиками. Типы завершения сверточных кодов включают «захват хвоста» и «сброс битов».

Существует много типов блочных кодов; Кодирование Рида-Соломона примечательно тем, что оно широко используется в компакт-дисках , DVD-дисках и жестких дисках . Другие примеры классических блочных кодов включают коды Голея , BCH , многомерной четности и коды Хэмминга .

Hamming ECC обычно используется для исправления ошибок флэш-памяти NAND . [6] Это обеспечивает коррекцию однобитных ошибок и обнаружение 2-битных ошибок. Коды Хэмминга подходят только для более надежных одноуровневых ячеек (SLC) NAND. Более плотная многоуровневая ячейка (MLC) NAND может использовать многобитовую корректирующую ECC, например BCH или Рида-Соломона. [7] [8] NOR Flash обычно не использует исправление ошибок. [7]

Классические блочные коды обычно декодируются с использованием жесткого решения . алгоритмов [9] это означает, что для каждого входного и выходного сигнала принимается жесткое решение, соответствует ли он единице или нулевому биту. Напротив, сверточные коды обычно декодируются с использованием алгоритмов мягкого решения, таких как алгоритмы Витерби, MAP или BCJR , которые обрабатывают (дискретизированные) аналоговые сигналы и которые обеспечивают гораздо более высокую производительность исправления ошибок, чем декодирование с жестким решением.

Почти все классические блочные коды применяют алгебраические свойства конечных полей . Поэтому классические блочные коды часто называют алгебраическими кодами.

В отличие от классических блочных кодов, которые часто предусматривают возможность обнаружения или исправления ошибок, многие современные блочные коды, такие как коды LDPC, не имеют таких гарантий. Вместо этого современные коды оцениваются с точки зрения частоты ошибок по битам.

Большинство кодов прямого исправления ошибок исправляют только перевороты битов, но не вставку или удаление битов. В этом случае расстояние Хэмминга является подходящим способом измерения частоты ошибок по битам . Несколько кодов прямого исправления ошибок предназначены для исправления вставки и удаления битов, например коды маркеров и коды водяных знаков. Расстояние Левенштейна является более подходящим способом измерения частоты ошибок по битам при использовании таких кодов. [10]

Скорость кода и компромисс между надежностью и передачи скоростью данных

См. Также: Скорость передачи данных § Скорость передачи информации.

Фундаментальный принцип ECC заключается в добавлении избыточных битов, чтобы помочь декодеру определить истинное сообщение, закодированное передатчиком. Скорость кода данной системы ECC определяется как соотношение между количеством информационных битов и общим количеством битов (т. е. информации плюс биты избыточности) в данном пакете связи. Следовательно, скорость кода является действительным числом. Низкая скорость кода, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, тогда как большая скорость кода, близкая к 1, подразумевает слабый код.

Избыточные биты, защищающие информацию, должны передаваться с использованием тех же ресурсов связи, которые они пытаются защитить. Это приводит к фундаментальному компромиссу между надежностью и скоростью передачи данных. [11] С одной стороны, сильный код (с низкой скоростью кодирования) может вызвать значительное увеличение SNR приемника (отношение сигнал/шум), уменьшая частоту ошибок по битам за счет снижения эффективной скорости передачи данных. С другой стороны, отсутствие использования ECC (т. е. кодовой скорости, равной 1) использует весь канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.

Интересен следующий вопрос: насколько эффективным с точки зрения передачи информации может быть ECC, имеющий пренебрежимо малую частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон с помощью своей второй теоремы, которая гласит, что пропускная способность канала — это максимальная скорость передачи данных, достижимая любым ECC, частота ошибок которого стремится к нулю: [12] Его доказательство основано на гауссовском случайном кодировании, которое не подходит для реальных приложений. Верхняя граница, полученная в работе Шеннона, вдохновила на долгий путь разработки ECC, который может приблизиться к предельной границе производительности. Различные коды сегодня могут достигать почти предела Шеннона. Однако реализация ECC для достижения пропускной способности обычно чрезвычайно сложна.

Наиболее популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных скоростей кода, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимизации влияния на скорость передачи данных. Другим критерием оптимизации скорости кодирования является баланс между низкой частотой ошибок и количеством повторных передач с учетом энергетических затрат на связь. [13]

коды ECC для Объединенные повышения производительности

Основная статья: Составные коды исправления ошибок

Классические (алгебраические) блочные коды и сверточные коды часто комбинируются в схемах каскадного кодирования, в которых сверточный код, декодированный по Витерби, с короткой длиной ограничения выполняет большую часть работы, и блочный код (обычно Рида – Соломона) с большим размером символа и длиной блока. «удаляет» любые ошибки, допущенные сверточным декодером. Однопроходное декодирование с использованием этого семейства кодов исправления ошибок может обеспечить очень низкую частоту ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.

Сцепленные коды стали стандартной практикой в ​​спутниковой связи и связи в дальнем космосе с тех пор, как «Вояджер-2» впервые использовал эту технику во время встречи с Ураном в 1986 году . Аппарат Галилео использовал итеративные каскадные коды, чтобы компенсировать очень высокую частоту ошибок, вызванную неисправной антенной.

четности низкой плотности ( Проверка LDPC )

Основная статья: Код проверки четности низкой плотности

Коды проверки четности низкой плотности (LDPC) представляют собой класс высокоэффективных линейных блоков. коды, состоящие из множества кодов одиночной проверки четности (SPC). Они могут обеспечить производительность, очень близкую к пропускной способности канала (теоретический максимум), используя метод итерационного декодирования с мягким решением, при линейной временной сложности с точки зрения длины блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.

Коды LDPC были впервые представлены Робертом Г. Галлагером в его докторской диссертации в 1960 году. но из-за вычислительных усилий по реализации кодера и декодера и введения кодов Рида – Соломона , их в основном игнорировали до 1990-х годов.

Коды LDPC в настоящее время используются во многих последних стандартах высокоскоростной связи, таких как DVB-S2 (цифровое видеовещание – спутник – второе поколение), WiMAX ( стандарт IEEE 802.16e для микроволновой связи), высокоскоростная беспроводная локальная сеть ( IEEE 802.11n) . ), [14] 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (стандарт ITU-T для организации сетей по линиям электропередачи, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в рамках 3GPP MBMS (см. исходные коды ).

Турбокоды [ править ]

Основная статья: Турбокод

Турбокодирование — это повторяющаяся схема мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до доли децибела от предела Шеннона . Предшествуя кодам LDPC с точки зрения практического применения, они теперь обеспечивают аналогичную производительность.

Одним из первых коммерческих применений турбокодирования была технология цифровой сотовой связи CDMA2000 1x (TIA IS-2000), разработанная Qualcomm и продаваемая Verizon Wireless , Sprint и другими операторами связи. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm и продается Verizon Wireless , Sprint и другими операторами связи (маркетинговое название 1xEV-DO от Verizon — Broadband Access , маркетинговые названия 1xEV-DO для потребителей и бизнеса — Power Vision и Mobile). Широкополосный доступ соответственно).

Локальное декодирование и тестирование кодов [ править ]

Основные статьи: Локально декодируемый код и Локально тестируемый код

Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и сделать это, не просматривая весь сигнал. Это может иметь смысл в условиях потоковой передачи, где кодовые слова слишком велики для достаточно быстрого классического декодирования и где на данный момент интерес представляют только несколько битов сообщения. Также такие коды стали важным инструментом в теории сложности вычислений , например, для разработки вероятностно проверяемых доказательств .

Локально декодируемые коды — это коды с исправлением ошибок, для которых отдельные биты сообщения могут быть вероятностно восстановлены, только рассматривая небольшое (скажем, постоянное) количество позиций кодового слова, даже после того, как кодовое слово было повреждено на некоторой постоянной доле позиций. Локально проверяемые коды — это коды с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, просматривая только небольшое количество позиций сигнала.

Не все коды тестирования осуществляют локальное декодирование и тестирование кодов.

Не все локально декодируемые коды (LDC) являются локально проверяемыми кодами (LTC). [15] ни локально корректируемых кодов (LCC), [16] LCC q-запроса ограничены экспоненциально [17] [18] в то время как НРС могут иметь субэкспоненциальную длину. [19] [20]

Чередование [ править ]

«Перемежитель» перенаправляется сюда. Чтобы узнать о волоконно-оптическом устройстве, см. оптический перемежитель .
Краткая иллюстрация идеи чередования

Чередование часто используется в цифровых системах связи и хранения для повышения производительности кодов прямого исправления ошибок. Многие каналы связи не лишены памяти: ошибки обычно возникают пакетами, а не независимо. Если количество ошибок в кодовом слове превышает возможности кода исправления ошибок, ему не удастся восстановить исходное кодовое слово. Чередование решает эту проблему, перетасовывая исходные символы по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок. [21] Поэтому чередование широко используется для исправления пакетов ошибок .

Анализ современных итерированных кодов, таких как турбокоды и коды LDPC , обычно предполагает независимое распределение ошибок. [22] Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов внутри кодового слова. [23]

Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности. [21] [24] нет коротких циклов Алгоритм итеративного декодирования работает лучше всего, когда в графе факторов , представляющем декодер, ; перемежитель выбран таким образом, чтобы избежать коротких циклов.

Конструкции перемежителя включают в себя:

  • прямоугольные (или равномерные) перемежители (аналогично методу с использованием коэффициентов пропуска, описанному выше)
  • сверточные перемежители
  • случайные перемежители (где перемежитель представляет собой известную случайную перестановку)
  • S-случайный перемежитель (где перемежитель представляет собой известную случайную перестановку с ограничением, что никакие входные символы на расстоянии S не появляются на расстоянии S на выходе). [25]
  • бесконкурентный квадратичный полином перестановки (QPP). [26] Примером использования является 3GPP Long Term Evolution . стандарт мобильной связи [27]

В системах связи с несколькими несущими перемежение по несущим может использоваться для обеспечения частотного разнесения , например, для уменьшения частотно-избирательного замирания или узкополосных помех. [28]

Пример [ править ]

Передача без чередования : 

Error-free message:                                 aaaabbbbccccddddeeeeffffgggg
Transmission with a burst error:                    aaaabbbbccc____deeeeffffgggg

Здесь каждая группа одной и той же буквы представляет собой 4-битное однобитовое кодовое слово, исправляющее ошибки. Кодовое слово cccc изменяется на один бит и может быть исправлено, но кодовое слово dddd изменяется на три бита, поэтому либо оно вообще не может быть декодировано, либо оно может быть декодировано неправильно .

С чередованием : 

Error-free code words:                              aaaabbbbccccddddeeeeffffgggg
Interleaved:                                        abcdefgabcdefgabcdefgabcdefg
Transmission with a burst error:                    abcdefgabcd____bcdefgabcdefg
Received code words after deinterleaving:           aa_abbbbccccdddde_eef_ffg_gg

В каждом из кодовых слов «аааа», «ееее», «фффф» и «гггг» изменяется только один бит, поэтому однобитный код исправления ошибок все правильно декодирует.

Передача без чередования : 

Original transmitted sentence:                      ThisIsAnExampleOfInterleaving
Received sentence with a burst error:               ThisIs______pleOfInterleaving

Термин «AnExample» в большинстве случаев оказывается непонятным и его трудно исправить.

С чередованием : 

Transmitted sentence:                               ThisIsAnExampleOfInterleaving...
Error-free transmission:                            TIEpfeaghsxlIrv.iAaenli.snmOten.
Received sentence with a burst error:               TIEpfe______Irv.iAaenli.snmOten.
Received sentence after deinterleaving:             T_isI_AnE_amp_eOfInterle_vin_...

Ни одно слово не потеряется полностью, а недостающие буквы можно восстановить с минимальными догадками.

Недостатки чередования [ править ]

Использование методов перемежения увеличивает общую задержку. Это связано с тем, что перед декодированием пакетов должен быть получен весь чередующийся блок. [29] Также перемежители скрывают структуру ошибок; без перемежителя более совершенные алгоритмы декодирования могут использовать структуру ошибок и обеспечить более надежную связь, чем более простой декодер в сочетании с перемежителем. [ нужна ссылка ] . Пример такого алгоритма основан на нейронной сети. [30] структуры.

Программное обеспечение для кодов, исправляющих ошибки [ править ]

Моделирование поведения кодов исправления ошибок (ECC) в программном обеспечении является обычной практикой проектирования, проверки и улучшения ECC. Грядущий стандарт беспроводной связи 5G открывает новый диапазон приложений для программных ECC: сети облачного радиодоступа (C-RAN) в контексте программно-определяемой радиосвязи (SDR) . Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программное обеспечение ECC может быть расположено в облаке, а антенны подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.

В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не исчерпывающее).

  • AFF3CT (A Fast Forward Error Correction Toolbox): полная коммуникационная цепочка на C++ (множество поддерживаемых кодов, таких как Turbo, LDPC, полярные коды и т. д.), очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
  • IT++ : библиотека классов и функций C++ для линейной алгебры, числовой оптимизации, обработки сигналов, связи и статистики.
  • OpenAir : реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.

Список кодов, исправляющих ошибки [ править ]

Расстояние Код
2 (обнаружение одиночной ошибки) Паритет
3 (исправление одиночных ошибок) Тройное модульное резервирование
3 (исправление одиночных ошибок) идеальный Хэмминг, такой как Хэмминг (7,4)
4 ( ОТДЕЛЕНО ) Расширенный Хэмминг
5 (исправление двойной ошибки)
6 (исправление двойной ошибки/обнаружение тройной ошибки) Код Нордстрома-Робинсона
7 (исправление трех ошибок) идеальный двоичный код Голея
8 (ТЕКФЕД) расширенный двоичный код Голея

См. также [ править ]

Ссылки [ править ]

  1. ^ Чарльз Ван; Дин Склар; Дайана Джонсон (зима 2001–2002 гг.). «Кодирование с прямым исправлением ошибок» . Перекрестная ссылка . 3 (1). Аэрокосмическая корпорация. Архивировано из оригинала 14 марта 2012 года . Проверено 5 марта 2006 г.
  2. ^ Чарльз Ван; Дин Склар; Дайана Джонсон (зима 2001–2002 гг.). «Кодирование с прямым исправлением ошибок» . Перекрестная ссылка . 3 (1). Аэрокосмическая корпорация. Архивировано из оригинала 14 марта 2012 года . Проверено 5 марта 2006 г. Как работают коды прямого исправления ошибок]
  3. ↑ Перейти обратно: Перейти обратно: а б Маундер, Роберт (2016). «Обзор канального кодирования» .
  4. ^ Гловер, Нил; Дадли, Трент (1990). Практическое проектирование коррекции ошибок для инженеров (редакция 1.1, 2-е изд.). Колорадо, США: Cirrus Logic . ISBN  0-927239-00-0 .
  5. ↑ Перейти обратно: Перейти обратно: а б Хэмминг, Ричард Уэсли (апрель 1950 г.). «Коды обнаружения и исправления ошибок». Технический журнал Bell System . 29 (2). США: AT&T : 147–160. дои : 10.1002/j.1538-7305.1950.tb00463.x . S2CID   61141773 .
  6. ^ «Коды Хэмминга для устройств флэш-памяти NAND». Архивировано 21 августа 2016 года на Wayback Machine . EE Times-Азия. По-видимому, основано на «Технической заметке Micron TN-29-08: Коды Хэмминга для устройств флэш-памяти NAND», заархивировано 29 августа 2017 года на Wayback Machine . 2005. Оба говорят: «Алгоритм Хэмминга — это общепринятый метод обнаружения и исправления ошибок во многих приложениях на основе флэш-памяти SLC NAND».
  7. ↑ Перейти обратно: Перейти обратно: а б «Какие типы ECC следует использовать во флэш-памяти?» (Примечание по применению) . Расширение. 2011. И алгоритм Рида-Соломона, и алгоритм BCH являются распространенными вариантами ECC для флэш-памяти MLC NAND. ... Блочные коды на основе Хэмминга являются наиболее часто используемыми ECC для SLC.... и Рид-Соломон, и BCH способны обрабатывать множественные ошибки и широко используются во флэш-памяти MLC.
  8. ^ Джим Кук (август 2007 г.). «Неудобная правда о флэш-памяти NAND» (PDF) . п. 28. Для SLC достаточно кода с порогом коррекции 1. требуется t=4... для MLC.
  9. ^ Балди, М.; Кьяралуче, Ф. (2008). «Простая схема декодирования кодов BCH и RS с распространением доверия в мультимедийных передачах» . Международный журнал цифрового мультимедийного вещания . 2008 : 1–12. дои : 10.1155/2008/957846 .
  10. ^ Шах, Гаурав; Молина, Андрес; Блейз, Мэтт (2006). «Клавиатуры и скрытые каналы» . УСЕНИКС . Проверено 20 декабря 2018 г.
  11. ^ Це, Дэвид; Вишванат, Прамод (2005), Основы беспроводной связи , издательство Кембриджского университета , Великобритания
  12. ^ Шеннон, CE (1948). «Математическая теория связи» (PDF) . Технический журнал Bell System . 27 (3–4): 379–423 и 623–656. дои : 10.1002/j.1538-7305.1948.tb01338.x . hdl : 11858/00-001M-0000-002C-4314-2 .
  13. ^ Росас, Ф.; Бранте, Г.; Соуза, РД; Оберли, К. (2014). «Оптимизация скорости передачи кода для достижения энергоэффективной беспроводной связи» . Материалы конференции IEEE по беспроводной связи и сетям (WCNC) . стр. 775–780. дои : 10.1109/WCNC.2014.6952166 . ISBN  978-1-4799-3083-8 .
  14. ^ Стандарт IEEE, раздел 20.3.11.6 «802.11n-2009». Архивировано 3 февраля 2013 г. в Wayback Machine , IEEE, 29 октября 2009 г., по состоянию на 21 марта 2011 г.
  15. ^ Кауфман, Тали ; Видерман, Майкл. «Локально проверяемые и локально декодируемые коды» .
  16. ^ Брубейкер, Бен (9 января 2024 г.). « Магическая» схема исправления ошибок оказалась по своей сути неэффективной» . Журнал Кванта . Проверено 9 января 2024 г.
  17. ^ Котари, Правеш К.; Манохар, Питер (2023). «Экспоненциальная нижняя граница для линейных локально корректируемых кодов с тремя запросами». arXiv : 2311.00558 [ cs.CC ].
  18. ^ Керенидис, Иорданис; де Вольф, Рональд (9 июня 2003 г.). «Экспоненциальная нижняя граница для локально декодируемых кодов с двумя запросами с помощью квантового аргумента» . Материалы тридцать пятого ежегодного симпозиума ACM по теории вычислений . АКМ. стр. 106–115. arXiv : Quant-ph/0208062 . дои : 10.1145/780542.780560 . ISBN  978-1-58113-674-6 . S2CID   10585919 .
  19. ^ Еханин, Сергей (февраль 2008 г.). «На пути к 3-запросным локально декодируемым кодам субэкспоненциальной длины» . Журнал АКМ . 55 (1): 1–16. дои : 10.1145/1326554.1326555 . ISSN   0004-5411 . S2CID   14617710 .
  20. ^ Ефременко, Клим (31 мая 2009 г.). «3-запросные локально декодируемые коды субэкспоненциальной длины» . Материалы сорок первого ежегодного симпозиума ACM по теории вычислений . АКМ. стр. 39–44. дои : 10.1145/1536414.1536422 . ISBN  978-1-60558-506-2 . S2CID   263865692 . {{cite book}}: |journal= игнорируется ( помогите )
  21. ↑ Перейти обратно: Перейти обратно: а б Вучетич, Б.; Юань, Дж. (2000). Турбокоды: принципы и применение . Спрингер Верлаг . ISBN  978-0-7923-7868-6 .
  22. ^ Луби, Майкл ; Митценмахер, М.; Шокроллахи, А.; Спилман, Д.; Стеманн, В. (1997). «Практические коды, устойчивые к потерям». Учеб. 29-й ежегодный симпозиум Ассоциации вычислительной техники (ACM) по теории вычислений .
  23. ^ «Цифровое видеовещание (DVB); структура кадра второго поколения, системы кодирования каналов и модуляции для радиовещания, интерактивных услуг, сбора новостей и других приложений спутникового широкополосного доступа (DVB-S2)». En 302 307 (Версия 1.2.1). ЕТСИ . Апрель 2009 года.
  24. ^ Эндрюс, Канзас; Дивсалар, Д.; Долинар, С.; Хэмкинс, Дж.; Джонс, ЧР; Поллара, Ф. (ноябрь 2007 г.). «Разработка кодов Turbo и LDPC для приложений дальнего космоса». Труды IEEE . 95 (11): 2142–2156. дои : 10.1109/JPROC.2007.905132 . S2CID   9289140 .
  25. ^ Долинар, С.; Дивсалар, Д. (15 августа 1995 г.). «Весовые распределения для турбокодов, использующих случайные и неслучайные перестановки». Отчет о ходе работы ТДА . 122 : 42–122. Бибкод : 1995ТДАПР.122...56Д . CiteSeerX   10.1.1.105.6640 .
  26. ^ Такешита, Оскар (2006). «Перемежители полиномов перестановок: алгебро-геометрическая перспектива». Транзакции IEEE по теории информации . 53 (6): 2116–2132. arXiv : cs/0601048 . Бибкод : 2006cs........1048T . дои : 10.1109/TIT.2007.896870 . S2CID   660 .
  27. ^ 3GPP TS 36.212 , версия 8.8.0, стр. 14
  28. ^ «Цифровое видеовещание (DVB); Структура кадра, кодирование каналов и модуляция для системы цифрового наземного телевизионного вещания второго поколения (DVB-T2)». EN 302 755 (Версия 1.1.1). ЕТСИ . Сентябрь 2009 года.
  29. ^ Техник (3 июня 2010 г.). «Объяснение чередования» . Технический блог W3 . Проверено 3 июня 2010 г.
  30. ^ Красстанов, Стефан; Цзян, Лян (8 сентября 2017 г.). «Вероятностный декодер глубоких нейронных сетей для кодов стабилизатора» . Научные отчеты . 7 (1): 11003. arXiv : 1705.09334 . Бибкод : 2017НатСР...711003К . дои : 10.1038/s41598-017-11266-1 . ПМК   5591216 . ПМИД   28887480 .
  31. ^ Нордстрем, AW; Робинсон, Дж. П. (1967), «Оптимальный нелинейный код», Information and Control , 11 (5–6): 613–616, doi : 10.1016/S0019-9958(67)90835-2.
  32. ^ Перри, Джонатан; Балакришнан, Хари; Шах, Деваврат (2011). «Безоценочные спинальные коды» . Материалы 10-го семинара ACM по актуальным темам в сетях . стр. 1–6. дои : 10.1145/2070562.2070568 . hdl : 1721.1/79676 . ISBN  9781450310598 .

Дальнейшее чтение [ править ]

Внешние ссылки [ править ]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Error_correction_code&oldid=1229637196#Forward_error_correction"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 26f88693de68acc25302f57bdae5bb2e__1718651880
URL1:https://arc.ask3.ru/arc/aa/26/2e/26f88693de68acc25302f57bdae5bb2e.html
Заголовок, (Title) документа по адресу, URL1:
Error correction code - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)