Отличный год
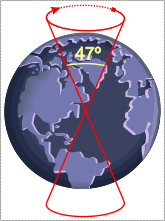
Термин «Великий год» имеет несколько основных значений. В научной астрономии он определяется как «Период одного полного цикла равноденствий вокруг эклиптики , или около 25 800 лет». Птолемей сообщал, что его учитель Гиппарх , сравнив положение точки весеннего равноденствия с положением неподвижных звезд в его время и в более ранних наблюдениях, обнаружил, что оно смещается к западу примерно на один градус каждые 72 года. Таким образом, время, которое понадобится равноденствию, чтобы совершить полный оборот через все зодиакальные созвездия и вернуться в исходное положение, составит примерно 25 920 лет. В гелиоцентрической модели прецессию можно представить как ось вращения Земли, совершающую медленный оборот вокруг нормали к плоскости эклиптики. Положение земной оси на северном ночном небе в настоящее время почти совпадает с Полярной звездой , Полярной звездой. Но так как направление оси меняется, то это мимолетное совпадение, которое не всегда было таким и не будет таким снова, пока не пройдет Великий Год.
Платоновский год , [1] который еще называют Великим годом, имеет иное, более древнее и мистическое значение. Платон предположил, что, вращая орбитальные движения Солнца, Луны и планет невооруженным глазом вперед или назад во времени, можно достичь точки, в которой они окажутся в тех же положениях, что и сегодня. Он назвал этот период времени Великим годом и предположил, что такое объединенное возвращение будет происходить примерно каждые 36 000 лет.
В более широком смысле термин «Великий год» можно использовать для обозначения любой концепции вечного возвращения в мировых мифологиях и философиях . Историк Отто Нойгебауэр пишет:
Трудность с термином «великий год» заключается в его двусмысленности. Почти любой период можно найти когда-нибудь или где-нибудь удостоенным этого имени. [2]
Описание науки
[ редактировать ]
Плоскость эклиптики — это плоскость, описываемая видимым движением Солнца на звездном фоне. Именно орбитальное движение Земли вокруг Солнца вызывает это кажущееся движение. Ось вращения Земли расположена не перпендикулярно этой плоскости, а под углом 23,5 градуса к перпендикуляру. Выравнивание оси сохраняется в течение года, так что точка неба над северным или южным полюсами остается неизменной на протяжении всего годового вращения Земли вокруг Солнца. [3]
Медленное коническое движение полярной оси Земли вокруг ее нормали к плоскости эклиптики вызвано силой притяжения других небесных тел на экваториальном выступе Земли. Подобное коническое движение можно наблюдать и в гироскопе, на который действуют боковые силы.
Результирующее движение оси Земли называется общей прецессией , и в результате точки равноденствия на эклиптике перемещаются на запад вдоль эклиптики со скоростью около 50,3 угловых секунды в год. Через 25 772 года точки снова оказались в той же точке неба, где начались наблюдения. [1]
Кроме того, наклон или наклон земной оси не является постоянным, а изменяется в собственном цикле. В течение цикла, составляющего в среднем около 40 000 лет, наклон оси варьируется от 22,1 до 24,5 градусов. [4]

История обоих определений
[ редактировать ]Платон (ок. 360 г. до н. э.) использовал термин «совершенный год» для описания возвращения небесных тел ( планет ) и суточного вращения неподвижных звезд (круга Одного и того же) в исходные положения; нет никаких доказательств того, что он знал об осевой прецессии . [5] Цикл, который описывает Платон, представляет собой цикл планетарного и астрального соединения, который можно постулировать, не осознавая осевой прецессии.
Гиппарх (ок. 120 г. до н. э.) — первый грек, которому приписывают открытие осевой прецессии примерно через двести лет после смерти Платона (см. Ниже).
Цицерон (I век до н. э.) вслед за Платоном определил Великий год как комбинацию солнечных, лунных и планетарных циклов. [6] [7]
Описание идеального года Платоном можно найти в его диалоге «Тимей» :
И поэтому люди почти не подозревают о том, что время на самом деле является блужданием этих тел, столь ошеломляюще многочисленных и поразительно разнообразных. Тем не менее, тем не менее возможно заметить, что совершенное число времени завершает совершенный год в тот момент, когда относительные скорости всех восьми периодов завершаются вместе и измеряются кругом Того же самого, который движется равномерно. , достигли своего завершения». [8]
в своей книге «О природе богов» Цицерон писал:
На разнообразном движении планет математики основали то, что они называют Великим Годом, «который завершается, когда Солнце, Луна и пять планет, закончив свои курсы, возвращаются в одни и те же положения относительно друг друга. период горячо обсуждается, но он обязательно должен быть фиксированным и определенным временем». [6]
Макробий » Цицерона (начало пятого века нашей эры) в своем комментарии к «Somnium Scipionis утверждает, что «философы» отсчитывают Великий Год за 15 000 лет. [9]
Цензорин (3 век нашей эры) писал, что Аристарх Самосский считал Великий год равным 2484 годам: но утверждалось, что это ошибочное копирование 2434 года, который представляет собой 45 Экселигма . циклов [9] [10]
Происхождение Платонического года, похоже, не имеет никакой связи с прецессией равноденствий, поскольку во времена Платона это было неизвестно. [11] Через два столетия после Платона Гиппарху приписывают открытие периода прецессии равноденствия . [12] и термин «Великий год» в конечном итоге стал применяться к периоду этой прецессии, вызванной медленным вращением оси Земли.
Примерно в середине второго века до нашей эры астроном Гиппарх обнаружил, что неподвижные звезды в целом постепенно смещают свое положение относительно ежегодно определяемых положений Солнца в дни равноденствий и солнцестояний... Отто Нойгебауэр утверждал, что Гиппарх в Факт считал, что это [36 000 лет] было максимальным показателем и что он также вычислил истинную скорость одного полного цикла прецессии, составляющую чуть менее 26 000 лет... [13]
Утверждается, что путаница между этими двумя понятиями возникла из-за астронома Птолемея (ок. 170 г. н. э.), который «принял более крупную, ошибочную цифру, в результате чего отныне две версии Великого года — Платонического Великого года — определялись планетами и прецессией, определяемой звездами, — все больше путались». [14]
Птолемея даже обвиняли в научном мошенничестве, когда он выдумывал наблюдения, которые дали бы цифру в 36 000 лет, хотя имеющиеся у него данные были достаточно хороши, чтобы очень близко приблизиться к истинной цифре в 26 000 лет. [15]
Иосиф Флавий (первый век нашей эры) говорит о «Великом году» ( древнегреческий : μέγας ἐνιαυτός ), длившемся 600 лет. [16]
Бог даровал им более длительный срок жизни из-за их добродетели и того, как они хорошо использовали ее в астрономических и геометрических открытиях, которые не дали бы времени для предсказания [периодов звезд], если бы они не прожили шестьсот лет. годы; ибо великий год завершается в этот промежуток времени. [16]
Было высказано предположение, что он получил это значение от Бероса (ок. III века до н.э.), который считал время с интервалами в 60, 600 и 3600 лет. [17]
Исаак Ньютон (1642–1726 /27 ) определил причину прецессии и установил скорость прецессии на уровне 1 градуса за 72 года, что очень близко к лучшему значению, измеренному сегодня, тем самым продемонстрировав величину ошибки в более раннем значении в 1 градус. в столетие. [18]
См. также
[ редактировать ]- Астрологический возраст - период времени в древних исторических и астрологических теориях времени.
- Осевая прецессия - Изменение оси вращения астрономического тела ( Прецессия § Астрономия )
- Юга - эпоха или эпоха в индуизме.
Ссылки
[ редактировать ]- ^ Jump up to: а б «Раздел G словаря по аэрокосмической науке и технологиям» . Hq.nasa.gov. 18 октября 1989 г. Архивировано из оригинала 21 апреля 2005 г. Проверено 2 марта 2014 г.
- ^ Нойгебауэр О., (1975) История древней математической астрономии , Биркхойзер, стр.618
- ^ «Раздел P словаря по аэрокосмической науке и технологиям» . www.hq.nasa.gov . Архивировано из оригинала 21 апреля 2005 г. Проверено 9 февраля 2019 г.
- ^ «Милутин Миланкович» . Earthobservatory.nasa.gov . 24 марта 2000 г. Проверено 15 февраля 2019 г.
- ^ Вуд, Майкл (24 июня 2010 г.). Платоновский год . Издательство Оксфордского университета. doi : 10.1093/acprof:oso/9780199557660.001.0001 . ISBN 9780191701726 .
- ^ Jump up to: а б Цицерон, О природе богов II.51 «Полный текст с английским переводом Х. Рэкхема» . 1933 год . Проверено 13 ноября 2019 г.
- ^ Николас Кэмпион, «Великий год: астрология, милленаризм и история в западной традиции» (Arkana/Penguin Books, 1994), стр. 6.
- ^ Платон, Тимей 39d, в книге Джона М. Купера (ред.), «Платон: Полное собрание сочинений» (Hackett Publishing Company, 1997), стр. 1243
- ^ Jump up to: а б Джей Ди Норт (1989). Звезды, разум и судьба: очерки древней и средневековой космологии . Академик Блумсбери. п. 96. ИСБН 978-0-907628-94-1 .
- ^ Аристарх и Система B 2002, DIO 11.1, 31 мая (стр. 6) Комментарии к свидетельствам Аристарха
- ^ Уильям Харрис Шталь, «Макробиус: комментарий к сну Сципиона» (издательство Колумбийского университета, 1952), стр. 21
- ^ «Раздел G словаря по аэрокосмической науке и технологиям» . Hq.nasa.gov. 18 октября 1989 г. Архивировано из оригинала 21 апреля 2005 г. Проверено 23 августа 2015 г.
- ^ Николас Кэмпион, «Великий год: астрология, милленаризм и история в западной традиции» (Arkana/Penguin Books, 1994), стр.246.
- ^ Николас Кэмпион, «Великий год: астрология, милленаризм и история в западной традиции» (Arkana/Penguin Books, 1994), стр. 246–247.
- ^ Р. Р. Ньютон, « Подлинность звездных данных Птолемея »
- ^ Jump up to: а б Иосиф Флавий – Иудейские древности – Книга I, Глава 3, Параграф 9
- ^ Иосиф Флавий, Еврейские древности , Леб, стр.1, примечание a.
- ^ «Справочники по истории Интернета» . Фордхэм.edu. п. письмо 17 . Проверено 2 марта 2014 г.
Дальнейшее чтение
[ редактировать ]- Каллатай, Г. де (1996). Аннус Платоник, Исследование мировых циклов в греко-латинских и арабских источниках . Лувен: Институт востоковедения Лувена.
- Кэмпион, Николас (1994). Великий год . Пингвин. ISBN 0140192964 .
- Кристофф, Борис (1981). Рока, Мартинес (ред.). Судьба человечества . Барселона: Коллекция Фонтана.
- Маквилли, Томас К. (2001). «Глава 3: Космический цикл». Форма древней мысли: сравнительные исследования греческой и индийской философии . Олворт. ISBN 1581152035 .