Осевая прецессия

Эта статья об астрономической концепции. О прецессии осей вне астрономии см. Прецессия . Чтобы узнать о неосевой астрономической прецессии, см. Астрономическую прецессию .

Прецессионное движение Земли. Земля вращается (белые стрелки) один раз в день вокруг своей оси вращения (красная); сама эта ось вращается медленно (белый кружок), совершая оборот примерно за 26 000 лет.

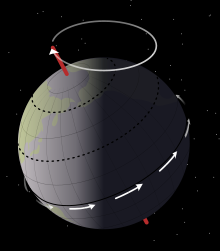
В астрономии тела . осевая прецессия — это вызванное гравитацией медленное и непрерывное изменение ориентации оси вращения астрономического В отсутствие прецессии орбита астрономического тела имела бы осевой параллелизм . В частности, осевая прецессия может относиться к постепенному сдвигу ориентации оси вращения Земли в цикле примерно 26 000 лет. Это похоже на прецессию волчка, ось которого описывает пару конусов, соединенных на вершинах . Термин «прецессия» обычно относится только к этой самой большой части движения; другие изменения в расположении земной оси — нутация и движение полюсов — гораздо меньшие по величине.

Прецессию Земли исторически называли прецессией равноденствий , поскольку точки равноденствия перемещались на запад вдоль эклиптики относительно неподвижных звезд , противоположно годовому движению Солнца по эклиптике. Исторически, Открытие прецессии равноденствий обычно приписывают на Западе астроному II века до нашей эры Гиппарху . С улучшением способности рассчитывать силу гравитации между планетами в первой половине девятнадцатого века было признано, что сама эклиптика слегка смещалась, что было названо планетарной прецессией , еще в 1863 году, в то время как доминирующий компонент был назван лунно-солнечной прецессией. . Их сочетание было названо общей прецессией , а не прецессией равноденствий.

Лунно-солнечная прецессия вызвана гравитационными силами Луны и Земли Солнца на экваториальной выпуклости , заставляющими ось Земли перемещаться относительно инерциального пространства . Планетарная прецессия (продвижение) возникает из-за небольшого угла между силой гравитации других планет на Земле и плоскостью ее орбиты (эклиптикой), в результате чего плоскость эклиптики слегка смещается относительно инерциального пространства. Лунно-солнечная прецессия примерно в 500 раз превышает планетарную прецессию. Помимо Луны и Солнца, другие планеты также вызывают небольшое перемещение оси Земли в инерциальном пространстве, из-за чего контраст между терминами лунно-солнечный и планетарный вводит в заблуждение, поэтому в 2006 году Международный астрономический союз рекомендовал переименовать доминирующий компонент в прецессию . экватора , а малую составляющую переименовали в прецессию эклиптики , но их совокупность по-прежнему называется общей прецессией. Многие ссылки на старые термины существуют в публикациях, предшествовавших изменению.

Номенклатура

Прецессия гироскопа ​ . Подобно тому, как сила стола порождает явление прецессии во вращающемся гироскопе, гравитационное притяжение Солнца и Луны на экваториальной выпуклости Земли вызывает очень медленную прецессию оси Земли (см. §Причина ). Это смещенное от центра толчок или притяжение вызывает крутящий момент, а крутящий момент на вращающемся теле приводит к прецессии. Гироскоп можно анализировать по частям, и каждая часть диска пытается упасть, но вращение перемещает ее снизу вверх, и конечным результатом прохождения всех частиц через это является прецессия.

Термин « прецессия » происходит от латинского praecedere («предшествовать, предшествовать или раньше»). Земли Видно, что звезды, наблюдаемые с Земли, движутся с востока на запад ежедневно из-за суточного движения и ежегодно из-за вращения Земли вокруг Солнца. В то же время можно наблюдать, как звезды слегка предвосхищают такое движение со скоростью примерно 50 угловых секунд в год - явление, известное как «прецессия равноденствий».

Описывая это движение, астрономы обычно сокращают этот термин до просто «прецессии». При описании причины движения физики также использовали термин «прецессия», что привело к некоторой путанице между наблюдаемым явлением и его причиной, что важно, поскольку в астрономии некоторые прецессии реальны, а другие очевидны. Этот вопрос еще больше запутывается тем фактом, что многие астрономы являются физиками или астрофизиками.

Термин «прецессия», используемый в астрономии, обычно описывает наблюдаемую прецессию точки равноденствия (звезды движутся ретроградно по небу), тогда как термин «прецессия», используемый в физике , обычно описывает механический процесс.

Эффекты

Совпадение годовых циклов апсид (ближайшего и дальнего приближения к Солнцу) и календарных дат (с указанием времен года) на четырех равноотстоящих друг от друга стадиях фиктивного прецессионного цикла в 20 000 лет (а не истинного прецессионного цикла Земли в 26 000 лет) ). Даты сезона указаны на севере. Наклон вымышленной оси Земли и эксцентриситет ее орбиты преувеличены. Приблизительные оценки. Эффекты слабой планетарной прецессии на показанных стадиях не учитываются.

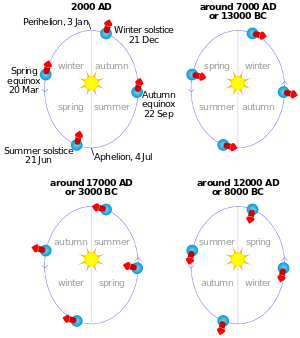
Прецессия земной оси имеет ряд наблюдаемых эффектов. Во-первых, кажется, что позиции южного и северного небесных полюсов движутся по кругу на неподвижном в пространстве фоне звезд, совершая один оборот примерно за 26 000 лет. звезда Таким образом, хотя сегодня Полярная лежит примерно на северном полюсе мира, со временем это изменится, и « полярной звездой » станут другие звезды. звезда Гамма Цефея Примерно через 3200 лет на эту позицию сменит в созвездии Цефея. На южном полюсе мира в настоящее время нет яркой звезды, которая бы отмечала его положение, но со временем прецессия также приведет к тому, что яркие звезды станут южными звездами . По мере смещения небесных полюсов происходит соответствующий постепенный сдвиг видимой ориентации всего звездного поля, если смотреть с определенной точки на Земле.

Во-вторых, положение Земли на ее орбите вокруг Солнца в дни солнцестояний , равноденствий или других времен года, определяемых относительно времен года, медленно меняется. Земли Например, предположим, что орбитальное положение Земли отмечается во время летнего солнцестояния, когда наклон оси направлен прямо к Солнцу. Спустя один полный оборот, когда Солнце вернулось в то же видимое положение относительно звезд на заднем плане, наклон оси Земли теперь не направлен прямо к Солнцу: из-за эффектов прецессии он немного «за пределами» этого. Другими словами, солнцестояние произошло немного раньше на орбите . Таким образом, тропический год , измеряющий цикл времен года (например, время от солнцестояния до солнцестояния или от равноденствия до равноденствия), примерно на 20 минут короче сидерического года , который измеряется видимым положением Солнца относительно звезд. . Примерно через 26 000 лет разница составит целый год, поэтому положения времен года относительно орбиты «вернутся туда, где они начались». (Другие эффекты также медленно меняют форму и ориентацию земной орбиты, и они в сочетании с прецессией создают различные циклы с разными периодами; см. также Циклы Миланковича . Величина наклона Земли, а не просто ее ориентация, также медленно меняется с течением времени, но этот эффект не объясняется непосредственно прецессией.)

По тем же причинам видимое положение Солнца относительно фона звезд в какое-то сезонно фиксированное время медленно регрессирует на полные 360° через все двенадцать традиционных созвездий зодиака со скоростью около 50,3 угловых секунды в год, или 1 градус каждые 71,6 года.

В настоящее время скорость прецессии соответствует периоду в 25772 года, поэтому тропический год короче сидерического года на 1224,5 секунды (20 мин 24,5 сек ≈ (365,24219×86400)/25772).

Сама скорость несколько меняется со временем (см. значения ниже), поэтому нельзя сказать, что ровно через 25 772 года ось Земли вернется туда, где она находится сейчас.

Более подробную информацию см. в разделах «Смена полярных звезд» и «Сдвиг полярностей и равноденствий» ниже.

История

Эллинистический мир

Гиппарх

Открытие прецессии обычно приписывают Гиппарху (190–120 до н. э.) Родосскому или Никейскому , греческому астроному . Согласно Птолемея » « Альмагесту , Гиппарх измерил долготу Спики и других ярких звезд. Сравнивая свои измерения с данными своих предшественников, Тимохариса (320–260 до н.э.) и Аристилла (~280 до н.э.), он пришел к выводу, что Спика сместилась на 2° относительно точки осеннего равноденствия . Он также сравнил продолжительность тропического года (время, необходимое Солнцу для возвращения к равноденствию) и сидерического года (время, необходимое Солнцу для возвращения к неподвижной звезде) и обнаружил небольшое несоответствие. Гиппарх пришел к выводу, что точки равноденствия перемещаются («прецессируют») по зодиаку и что скорость прецессии составляет не менее 1° за столетие, иными словами, совершая полный цикл не более чем за 36 000 лет.

Практически все сочинения Гиппарха утеряны, включая его работы по прецессии. О них упоминает Птолемей, который объясняет прецессию вращением небесной сферы вокруг неподвижной Земли. Разумно предположить, что Гиппарх, подобно Птолемею, мыслил прецессию в геоцентрических терминах как движение неба, а не Земли.

Птолемей

Первым астрономом, который, как известно, продолжил работу Гиппарха по прецессии, был Птолемей, живший во втором веке нашей эры. Птолемей измерил долготу Регула , Спики и других ярких звезд вариацией лунного метода Гиппарха, не требующей затмений. Перед закатом он измерил продольную дугу, отделяющую Луну от Солнца. Затем, после захода солнца, он измерил дугу от Луны до звезды. Он использовал модель Гиппарха для расчета долготы Солнца и внес поправки на движение Луны и ее параллакс . Птолемей сравнил свои наблюдения с наблюдениями Гиппарха, Менелая Александрийского , Тимохариса и Агриппы . Он обнаружил, что между временем Гиппарха и его собственным (около 265 лет) звезды сместились на 2°40', или 1° за 100 лет (36" в год; принятая сегодня скорость составляет около 50" в год или 1° в год). 72 года). Однако возможно, что Птолемей просто доверился фигуре Гиппарха вместо того, чтобы провести собственные измерения. Он также подтвердил, что прецессия затронула все неподвижные звезды, а не только те, которые находятся вблизи эклиптики, и его цикл имел тот же период в 36 000 лет, что и цикл Гиппарха.

Другие авторы

Большинство древних авторов о прецессии не упоминали и, возможно, не знали о ней. Например, Прокл отверг прецессию, а Теон Александрийский , комментатор Птолемея в четвертом веке, принял объяснение Птолемея. Теон также сообщает альтернативную теорию:

«По некоторым мнениям древние астрологи полагают, что с известной эпохи знаки солнцестояния совершают движение на 8° в порядке знаков, после чего возвращаются на такое же расстояние назад...» (Дрейер 1958, стр. 204)

Вместо того, чтобы пройти всю зодиакальную последовательность, точки равноденствия «трепетали» взад и вперед по дуге в 8°. Теория трепета представлена ​​Теоном как альтернатива прецессии.

Альтернативные теории открытий

вавилоняне

Были сделаны различные утверждения, что другие культуры открыли прецессию независимо от Гиппарха. По словам Аль-Баттани , халдейские астрономы разделили тропический и сидерический год так, что примерно к 330 г. до н.э. они были в состоянии описать прецессию, хотя и неточно, но такие утверждения обычно считаются необоснованными.

Майя

Археолог Сьюзан Милбрат предположила, что мезоамериканский календарь длинного счета на «30 000 лет с участием Плеяд … мог быть попыткой вычислить прецессию равноденствия». Этой точки зрения придерживаются немногие другие профессиональные исследователи цивилизации майя .

Древние египтяне

Точно так же утверждается, что прецессия равноденствий была известна в Древнем Египте до времен Гиппарха ( период Птолемеев ). Эти утверждения остаются спорными. Древние египтяне вели точные календари и записывали даты на стенах храмов, поэтому им было несложно построить «грубую» скорость прецессии.

Дендерский зодиак , звездная карта внутри храма Хатхор в Дендере , предположительно фиксирует прецессию равноденствий. В любом случае, если древние египтяне и знали о прецессии, их знания не зафиксированы как таковые ни в одном из сохранившихся астрономических текстов.

Майкл Райс, популярный писатель о Древнем Египте, писал, что древние египтяне, должно быть, наблюдали прецессию. и предположили, что это осознание оказало глубокое влияние на их культуру. Райс отметила, что египтяне изменили ориентацию храмов в ответ на прецессию связанных звезд.

Индия

До 1200 года в Индии существовало две теории трепета : одна со скоростью, другая без скорости, а также несколько связанных моделей прецессии. В каждом из них были незначительные изменения или исправления, внесенные различными комментаторами. Доминирующим из трех был трепет, описанный в самом уважаемом индийском астрономическом трактате « Сурья Сиддханта» (3:9–12), составленном ок. 400 , но пересмотрен в течение следующих нескольких столетий. В нем использовалась сидерическая эпоха, или аянамса , которая до сих пор используется во всех индийских календарях , и варьируется по эклиптической долготе от 19 ° 11 'до 23 ° 51', в зависимости от группы, с которой консультировались. В эту эпоху примерно 30 индийских календарных лет начинаются через 23–28 дней после современного мартовского равноденствия . Мартовское равноденствие Сурья Сиддханты отклонилось на 27° в обе стороны от сидерической эпохи. Таким образом, точка равноденствия сместилась на 54° в одном направлении, а затем назад на 54° в другом направлении. Этот цикл занял 7200 лет со скоростью 54 дюйма в год. Равноденствие совпало с эпохой начала Кали-юги в -3101 году и снова 3600 лет спустя, в 499 году. Направление изменилось с прямого на ретроградное на полпути между этими годами в -1301 году, когда оно достигло максимального отклонения в 27 °, и будет оставались ретроградными, в том же направлении, что и современная прецессия, в течение 3600 лет до 2299 года.

Другой трепет описал Варахамихира ( ок. 550 г.). Его трепет заключался в дуге 46°40′ в одном направлении и возвращении в исходную точку. Половина этой дуги, 23°20′, соответствует максимальному склонению Солнца по обе стороны от экватора в дни солнцестояний. Однако период не был указан, поэтому определить годовую ставку невозможно.

Некоторые авторы описывают прецессию как около 200 000   оборотов за кальпу длительностью 4 320 000 000   лет, что соответствует скорости ⁠ 200 000×360×3600 / 4 320 000 000 ⁠   = 60 дюймов/год. Вероятно, они отклонились даже от 200 000   оборотов, чтобы сделать накопленную прецессию равной нулю около 500. Вишнучандра ( ок. 550–600 ) упоминает 189 411   оборотов в Кальпе или 56,8 дюймов в год. Бхаскара I ( ок. 600–680 ) упоминает [1] 94 110   оборотов в кальпе или 58,2 дюйма в год. Бхаскара II ( ок. 1150 г. ) упоминает 199 699   оборотов за кальпу, или 59,9 дюймов в год.

Китайская астрономия

Юй Си (четвертый век нашей эры) был первым китайским астрономом, упомянувшим прецессию. Он оценил скорость прецессии в 1° за 50 лет.

Средневековье и Возрождение

В средневековой исламской астрономии Птолемея прецессия была известна на основе «Альмагеста» и наблюдений, уточнивших ее значение.

Аль-Баттани в своей работе Зидж Аль-Саби упоминает расчет прецессии Гиппарха, а значение Птолемея в 1 градус на 100 солнечных лет говорит, что он измерил прецессию и нашел ее равной одному градусу на 66 солнечных лет.

Впоследствии Аль-Суфи в своей «Книге неподвижных звезд » упоминает те же значения, что и значение прецессии Птолемея — 1 градус на 100 солнечных лет. Затем он цитирует другое значение из Зидж Аль Мумтахана , которое было сделано во время Аль-Мамуна правления : 1 градус на каждые 66 солнечных лет. Он также цитирует вышеупомянутого Зиджа Аль-Саби из Аль-Баттани, который скорректировал координаты звезд на 11 градусов и 10 угловых минут, чтобы учесть разницу между временем Аль-Баттани и временем Птолемея.

Позднее « Зидж-и Ильхани» , составленная в обсерватории Мараге , устанавливает прецессию равноденствий на уровне 51 угловой секунды в год, что очень близко к современному значению в 50,2 угловых секунды.

В средние века исламские и латинско-христианские астрономы рассматривали «трепет» как движение неподвижных звезд, добавляемое к прецессии. Эту теорию обычно приписывают арабскому астроному Сабиту ибн Курре , но в наше время эта теория оспаривается. Николай Коперник опубликовал другое описание трепета в книге De Revolutionibus orbium coelestium (1543 г.). В этой работе впервые четко упоминается прецессия как результат движения земной оси. Коперник охарактеризовал прецессию как третье движение Земли.

Современный период

Более века спустя Исаак Ньютон в «Philosophiae Naturalis Principia Mathematica» (1687) объяснил прецессию следствием гравитации . Однако оригинальные уравнения прецессии Ньютона не работали и были значительно пересмотрены Жаном ле Роном д'Аламбером и последующими учёными.

Открытие Гиппарха

Гиппарх описал свое открытие в книге «О смещении точек солнцестояния и равноденствия» (описанной в «Альмагесте» III.1 и VII.2). Он измерил эклиптическую долготу звезды Спика во время лунных затмений и обнаружил, что она находится примерно в 6° к западу от точки осеннего равноденствия . Сравнивая свои собственные измерения с измерениями Тимохариса Александрийского (современника Евклида , работавшего с Аристиллом в начале III века до нашей эры), он обнаружил, что долгота Спики за это время уменьшилась примерно на 2° (точные годы в Альмагест ). Также в VII.2 Птолемей приводит более точные наблюдения за двумя звездами, включая Спику, и приходит к выводу, что в каждом случае изменение на 2°40' произошло между 128 г. до н.э. и 139 г. н.э. Следовательно, 1° за столетие или один полный цикл из 36 000 лет. годы, то есть период прецессии Гиппарха, как сообщает Птолемей; ср. страница 328 в переводе Тумера «Альмагеста», издание 1998 года. Он также заметил это движение и у других звезд. Он предположил, что со временем смещались только звезды вблизи зодиака. Птолемей назвал это своей «первой гипотезой» ( Альмагест VII.1), но не сообщил о какой-либо более поздней гипотезе, которую мог бы разработать Гиппарх. Гиппарх, видимо, ограничил свои рассуждения, поскольку располагал лишь несколькими более старыми наблюдениями, не отличавшимися большой достоверностью.

Поскольку точки равноденствия не отмечены на небе, Гиппарху нужна была Луна в качестве ориентира; он использовал лунное затмение , чтобы измерить положение звезды. Гиппарх уже разработал способ расчета долготы Солнца в любой момент. Лунное затмение происходит во время Полнолуния , когда Луна находится в оппозиции , ровно на 180° от Солнца. Считается, что Гиппарх измерил продольную дугу, отделяющую Спику от Луны. К этому значению он добавил рассчитанную долготу Солнца плюс 180° к долготе Луны. Он проделал ту же процедуру с данными Тимохариса. Наблюдения, подобные этим затмениям, кстати, являются основным источником данных о том, когда работал Гиппарх, поскольку другие биографические сведения о нем минимальны. Лунные затмения, которые он наблюдал, например, произошли 21 апреля 146 г. до н.э. и 21 марта 135 г. до н.э.

Гиппарх также изучал прецессию в «О длине года» . Два вида года имеют отношение к пониманию его творчества. Тропический год — это отрезок времени, который требуется Солнцу, если смотреть с Земли, чтобы вернуться в то же положение по эклиптике (свой путь среди звезд на небесной сфере). Сидерический год — это отрезок времени, который требуется Солнцу, чтобы вернуться в то же положение относительно звезд небесной сферы. Прецессия заставляет звезды немного менять свою долготу каждый год, поэтому сидерический год длиннее тропического. Используя наблюдения за равноденствиями и солнцестояниями, Гиппарх установил, что продолжительность тропического года составляет 365+1/4-1/300 дней, или 365,24667 дней (Эванс 1998, стр. 209). Сравнивая это с длиной сидерического года, он вычислил, что скорость прецессии составляла не менее 1° в столетие. По этой информации можно подсчитать, что его значение для сидерического года составило 365+1/4+1/144 дня. Указывая минимальную скорость, он, возможно, допускал ошибки в наблюдении.

Чтобы приблизиться к своему тропическому году, Гиппарх создал свой собственный лунно-солнечный календарь , изменив календарь Метона и Каллиппа в «О вставных месяцах и днях » (ныне утерянных), как описано Птолемеем в « Альмагесте III.1». В вавилонском календаре использовался цикл из 235 лунных месяцев за 19 лет, начиная с 499 г. до н. э. (только с тремя исключениями до 380 г. до н. э.), но в нем не использовалось определенное количество дней. Цикл Метона (432 г. до н.э.) отводил этим 19 годам 6940 дней, в результате чего средний год составлял 365+1/4+1/76 или 365,26316 дней. Каллиппический цикл (330 г. до н. э.) сократился на один день по сравнению с четырьмя циклами Метоника (76 лет), в среднем год составлял 365 + 1/4 или 365,25 дней. Гиппарх сократил еще один день из четырех каллиппических циклов (304 года), создав цикл Гиппарха со средней продолжительностью года 365+1/4-1/304 или 365,24671 дня, что было близко к его тропическому году 365+1/4-. 1/300 или 365,24667 дней.

Математические подписи Гиппарха найдены в Антикитерском механизме , древнем астрономическом компьютере второго века до нашей эры. Механизм основан на солнечном году, Метоническом цикле, который представляет собой период повторного появления Луны в том же месте на небе с той же фазой (полная Луна появляется в том же месте на небе примерно через 19 лет), Каллипическом цикле. цикл (который составляет четыре цикла Метоника и более точный), цикл Сароса и циклы Экселигмоса (три цикла Сароса для точного предсказания затмения). Изучение Антикиферского механизма показало, что древние использовали очень точные календари, основанные на всех аспектах движения Солнца и Луны на небе. Фактически, Лунный механизм, который является частью Антикиферского механизма, изображает движение Луны и ее фазу в течение заданного времени, используя цепь из четырех шестерен со штифтом и пазом, что дает переменную лунную скорость, очень близкую к ко второму закону Кеплера . То есть учитывается быстрое движение Луны на перигей и замедленное движение в апогее .

Смена полярных звезд

Прецессия земной оси вокруг северного полюса эклиптики.

Следствием прецессии является изменение полярной звезды . В настоящее время Полярная звезда очень хорошо подходит для обозначения положения северного полюса мира, поскольку Полярная звезда представляет собой умеренно яркую звезду с визуальной величиной 2,1 (переменная) и расположена примерно в одном градусе от полюса, и звезд такой же яркости тоже нет. закрывать.

Прецессия земной оси вокруг южного полюса эклиптики.

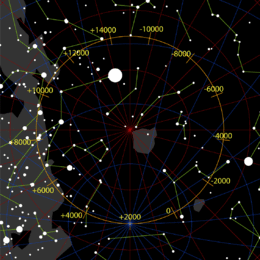
Предыдущей полярной звездой была Кохаб (Бета Малой Медведицы, β UMi, β Малой Медведицы), ярчайшая звезда в чаше «Малого Ковша», расположенная в 16 градусах от Полярной звезды. Он занимал эту роль с 1500 г. до н. э. по 500 г. н. э. В свое время он был не таким точным, как Polaris сегодня. Сегодня Кохаб и его сосед Феркад называют «Хранителями полюса» (имеется в виду Полярная звезда).

С другой стороны, Тубан в созвездии Дракона , который был полярной звездой в 3000 году до нашей эры, гораздо менее заметен со звездной величиной 3,67 (одна пятая яркости Полярной звезды); сегодня он невидим в засветленном городском небе.

Когда Полярная звезда снова станет северной звездой около 27 800 г., она будет находиться дальше от полюса, чем сейчас, из-за своего собственного движения , в то время как в 23 600 г. до н. э. она подошла ближе к полюсу.

В этот момент труднее найти на небе южный полюс мира, поскольку эта область представляет собой особенно мягкий участок неба. Номинальная звезда южного полюса — Сигма Октантис , звездная величина 5,5 едва видна невооруженным глазом даже в идеальных условиях. Однако ситуация изменится с 80-го по 90-й века, когда южный полюс мира пройдет через Ложный Крест .

Эта ситуация также видна на звездной карте. Ориентация Южного полюса движется в сторону созвездия Южного Креста . Последние 2000 лет или около того Южный Крест указывал на южный полюс мира. Как следствие, созвездие трудно увидеть из субтропических северных широт, в отличие от времен древних греков . Южный Крест можно увидеть даже с севера, вплоть до Майами (около 25° с.ш.), но только зимой/ранней весной.

Сдвиг полюсов и смещение равноденствий

Прецессионное движение, как видно «снаружи» небесной сферы

25700-летний цикл прецессии, вид с Земли. Нынешняя северная полярная звезда — Полярная (вверху). Примерно через 8 000 лет это будет яркая звезда Денеб (слева), а примерно через 12 000 лет — Вега (слева в центре). Вращение Земли изображено не в масштабе — за этот промежуток времени она фактически повернулась бы более 4 миллионов раз.

Изображения справа пытаются объяснить связь между прецессией земной оси и сдвигом точек равноденствия. Эти изображения показывают положение оси Земли на небесной сфере , воображаемой сфере, на которой звезды располагаются в соответствии с их положением, видимым с Земли, независимо от их фактического расстояния. На первом изображении небесная сфера видна снаружи, а созвездия расположены в зеркальном отражении. На втором изображении показана перспектива околоземной позиции, если смотреть через очень широкоугольный объектив (из-за которого возникает кажущееся искажение).

Ось вращения Земли за период в 25 700 лет описывает небольшой синий круг среди звезд в верхней части диаграммы с центром на северном полюсе эклиптики ( синяя буква E ) и с угловым радиусом около 23,4 °. угол, известный как наклон эклиптики . Направление прецессии противоположно суточному вращению Земли вокруг своей оси. Коричневая ось была осью вращения Земли 5000 лет назад, когда она указывала на звезду Тубан . Желтая ось, указывающая на Полярную звезду, теперь отмечает ось.

Равноденствия происходят там, где небесный экватор пересекает эклиптику (красную линию), то есть там, где ось Земли перпендикулярна линии, соединяющей центры Солнца и Земли. Термин «равноденствие» здесь относится к точке на небесной сфере. определяется таким образом, а не момент времени, когда Солнце находится над экватором (хотя эти два значения связаны). Когда ось прецессирует из одной ориентации в другую, экваториальная плоскость Земли (обозначенная круговой сеткой вокруг экватора) перемещается. Небесный экватор — это всего лишь экватор Земли, проецированный на небесную сферу, поэтому он движется так же, как движется экваториальная плоскость Земли, и точка пересечения с эклиптикой движется вместе с ней. Положения полюсов и экватора на Земле не меняются, меняется только ориентация Земли относительно неподвижных звезд.

Диаграмма, показывающая смещение мартовского равноденствия звезд на запад за последние 6000 лет.

Как видно по коричневой сетке , 5000 лет назад мартовское равноденствие находилось недалеко от звезды Альдебаран в Тельце . Теперь, как видно по желтой сетке, оно сместилось (показано красной стрелкой ) куда-то в созвездие Рыб .

Подобные стоп-кадры являются лишь первыми приближениями, так как они не учитывают переменную скорость прецессии, переменный наклон эклиптики, планетарную прецессию (которая представляет собой медленное вращение самой плоскости эклиптики , в настоящее время вокруг оси, расположенной на плоскости с долготой 174,8764°) и собственные движения звезд.

Прецессионные эры каждого созвездия, часто называемые « Великими Месяцами », приведены примерно в таблице ниже:

Созвездие	Приблизительный год
	Вход	Выход
Телец	4500 г. до н.э.	2000 г. до н.э.
Овен	2000 г. до н.э.	100 г. до н.э.
Рыбы	100 г. до н.э.	2700 г. н. э.

Причина

Прецессия равноденствий вызвана силами гравитации Солнца и Луны и в меньшей степени других тел на Земле. Впервые это объяснил сэр Исаак Ньютон .

Осевая прецессия аналогична прецессии волчка. В обоих случаях приложенная сила возникает под действием силы тяжести. Для волчка эта сила изначально имеет тенденцию быть почти параллельной оси вращения и увеличивается по мере замедления волчка. Для гироскопа на стойке он может приближаться к 90 градусам. Однако для Земли приложенные силы Солнца и Луны ближе к перпендикуляру оси вращения.

Земля представляет собой не идеальную сферу, а сплюснутый сфероид , экваториальный диаметр которого примерно на 43 километра превышает ее полярный диаметр. Земли Из-за наклона оси в течение большей части года половина этой выпуклости, ближайшая к Солнцу, смещена от центра либо на север, либо на юг, а дальняя половина — на противоположную сторону. Гравитационное притяжение на ближней половине сильнее, поскольку гравитация уменьшается пропорционально квадрату расстояния, поэтому это создает небольшой крутящий момент на Земле, поскольку Солнце притягивает сильнее с одной стороны Земли, чем с другой. Ось этого крутящего момента примерно перпендикулярна оси вращения Земли, поэтому ось вращения прецессирует . Если бы Земля была идеальной сферой, прецессии не было бы.

Этот средний крутящий момент перпендикулярен направлению, в котором ось вращения наклонена от полюса эклиптики, так что он не меняет сам осевой наклон. Величина крутящего момента Солнца (или Луны) зависит от угла между направлением оси вращения Земли и направлением гравитационного притяжения. Оно приближается к нулю, когда они перпендикулярны. Например, это происходит в дни равноденствий в случае взаимодействия с Солнцем. Это можно увидеть, поскольку ближняя и дальняя точки совпадают с гравитационным притяжением, поэтому крутящий момент отсутствует из-за разницы в гравитационном притяжении.

Хотя приведенное выше объяснение касалось Солнца, то же объяснение справедливо и для любого объекта, движущегося вокруг Земли вдоль эклиптики или близко к ней, особенно для Луны. Совместное действие Солнца и Луны называется лунно-солнечной прецессией. В дополнение к устойчивому поступательному движению (приводящему к полному обороту примерно за 25 700 лет) Солнце и Луна также вызывают небольшие периодические изменения из-за их изменения положения. Эти колебания, как скорости прецессии, так и осевого наклона, известны как нутация . Самый важный термин имеет период 18,6 лет и амплитуду 9,2 угловых секунды.

Помимо лунно-солнечной прецессии, действия других планет Солнечной системы заставляют всю эклиптику медленно вращаться вокруг оси, эклиптическая долгота которой составляет около 174 °, измеренная на мгновенной эклиптике. Этот так называемый сдвиг планетарной прецессии представляет собой поворот плоскости эклиптики на 0,47 угловой секунды в год (более чем в сто раз меньше, чем лунно-солнечная прецессия). Сумма двух прецессий известна как общая прецессия.

Уравнения

Приливная сила на Земле, вызванная Луной или другим небесным телом. На нем показано как приливное поле (толстые красные стрелки), так и гравитационное поле (тонкие синие стрелки), действующие на поверхность и центр Земли (метка O) со стороны Луны (метка S).

Приливная сила на Земле, вызываемая возмущающим телом (Солнцем, Луной или планетой), выражается законом всемирного тяготения Ньютона , согласно которому гравитационная сила возмущающего тела на ближайшей к Земле стороне считается большей, чем гравитационная сила на Земле. дальнюю сторону на величину, пропорциональную разности кубов расстояний между ближней и дальней сторонами. действующую на массу Земли как точечную массу в центре Земли (которая обеспечивает центростремительную силу, Если из гравитационной силы возмущающего тела повсюду на поверхности Земли вычесть гравитационную силу возмущающего тела, вызывающую орбитальное движение). Земля, то, что осталось, можно рассматривать как приливную силу. Это дает парадоксальное представление о силе, действующей в направлении от спутника, но на самом деле это просто меньшая сила, направленная к этому телу из-за градиента гравитационного поля. Для прецессии эту приливную силу можно сгруппировать в две силы, которые действуют только на экваториальную выпуклость. за пределами среднего сферического радиуса. Эту пару можно разложить на две пары компонентов: одну пару, параллельную экваториальной плоскости Земли в направлении и от возмущающего тела, которые компенсируют друг друга, и другую пару, параллельную оси вращения Земли, обе в направлении плоскости эклиптики . Последняя пара сил создает следующий крутящего момента вектор на экваториальной выпуклости Земли:

${\overrightarrow {T}}={\frac {3GM}{r^{3}}}(C-A)\sin \delta \cos \delta {\begin{pmatrix}\sin \alpha \\-\cos \alpha \\0\end{pmatrix}}$

где

GM , стандартный гравитационный параметр возмущающего тела

r , геоцентрическое расстояние до возмущающего тела

C , момент инерции вокруг оси вращения Земли.

A — момент инерции вокруг любого экваториального диаметра Земли.

C − A , момент инерции экваториальной выпуклости Земли ( C > A )

δ , склонение возмущающего тела (к северу или югу от экватора)

α — прямое восхождение возмущающего тела (восточнее от мартовского равноденствия ).

Три единичных вектора крутящего момента в центре Земли (сверху вниз) — это x на линии внутри плоскости эклиптики (пересечение экваториальной плоскости Земли с плоскостью эклиптики), направленной к мартовскому равноденствию, y на линии в плоскость эклиптики направлена ​​к месту летнего солнцестояния (90° к востоку от x ), а z - на линии, направленной к северному полюсу эклиптики.

Значение трех синусоидальных членов в направлении x (sin δ cos δ sin α ) для Солнца представляет собой синусоидальную форму волны, изменяющуюся от нуля в дни равноденствий (0 °, 180 °) до 0,36495 в дни солнцестояний (90 °, 270°). Значение в направлении y (sin δ cos δ (−cos α )) для Солнца представляет собой синусоидальную волну, изменяющуюся от нуля в дни четырех равноденствий и солнцестояний до ±0,19364 (чуть больше половины пика синусоидального квадрата) на полпути между каждое равноденствие и солнцестояние с пиками, слегка смещенными к точкам равноденствия (43,37 ° (-), 136,63 ° (+), 223,37 ° (-), 316,63 ° (+)). Обе формы солнечных волн имеют примерно одинаковую размах амплитуды и одинаковый период: половину оборота или половину года. Значение в направлении z равно нулю.

Средний момент синусоиды в направлении y равен нулю для Солнца или Луны, поэтому эта составляющая момента не влияет на прецессию. Средний крутящий момент синусоидального сигнала в направлении x для Солнца или Луны составляет:

$T_{x}={\frac {3}{2}}{\frac {GM}{a^{3}\left(1-e^{2}\right)^{\frac {3}{2}}}}(C-A)\sin \epsilon \cos \epsilon$

где

$a$, большая полуось орбиты Земли (Солнца) или орбиты Луны

e , эксцентриситет орбиты Земли (Солнца) или орбиты Луны.

а 1/2 соответствует среднему значению синусоидального сигнала, $a^{3}\left(1-e^{2}\right)^{\frac {3}{2}}$ составляет среднее кубическое расстояние Солнца или Луны от Земли по всей эллиптической орбите, а ε (угол между плоскостью экватора и плоскостью эклиптики) — максимальное значение δ для Солнца и среднее максимальное значение для Луны за весь 18,6-летний цикл.

Прецессия – это:

${\frac {d\psi }{dt}}={\frac {T_{x}}{C\omega \sin \epsilon }}$

где ω Земли — угловая скорость , а Cω Земли — угловой момент . Таким образом, составляющая первого порядка прецессии Солнца равна:

${\frac {d\psi _{S}}{dt}}={\frac {3}{2}}\left[{\frac {GM}{a^{3}\left(1-e^{2}\right)^{\frac {3}{2}}}}\right]_{S}\left[{\frac {C-A}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}$

тогда как из-за Луны это:

${\frac {d\psi _{L}}{dt}}={\frac {3}{2}}\left[{\frac {GM\left(1-1.5\sin ^{2}i\right)}{a^{3}\left(1-e^{2}\right)^{\frac {3}{2}}}}\right]_{L}\left[{\frac {C-A}{C}}{\frac {\cos \epsilon }{\omega }}\right]_{E}$

где i - угол между плоскостью орбиты Луны и плоскостью эклиптики. В этих двух уравнениях параметры Солнца находятся в квадратных скобках, обозначенных S, параметры Луны находятся в квадратных скобках, обозначенных L, а параметры Земли находятся в квадратных скобках, обозначенных E. Термин $\left(1-1.5\sin ^{2}i\right)$ объясняет наклон орбиты Луны относительно эклиптики. Термин ( C − A )/ C Земли представляет собой динамическую эллиптичность или уплощение , которая корректируется с учетом наблюдаемой прецессии, поскольку внутренняя структура Земли не известна достаточно подробно. Если бы Земля была однородной, этот член был бы равен квадрату ее третьего эксцентриситета .

$e''^{2}={\frac {\mathrm {a} ^{2}-\mathrm {c} ^{2}}{\mathrm {a} ^{2}+\mathrm {c} ^{2}}}$

где a — экваториальный радиус ( 6  378  137 м ), а c — полярный радиус ( 6  356  752 м ), поэтому e ² = 0.003358481 .

Применимые параметры для J2000.0, округленные до семи значащих цифр (исключая ведущую 1):

Солнце	Луна	Земля
ГМ = 1,3271244 × 10 20 м 3 /с 2	ГМ = 4,902799 × 10 12 м 3 /с 2	( С - А )/ С = 0,003273763
	а = 3,833978 × 10 8 м	а = 1,4959802 × 10 11 м
	е = 0,05554553	е = 0,016708634
	я = 5,156690°	ε = 23,43928°
		ω = 7,292115 × 10 −5 рад/с

которые дают

dψ _S /dt = 2,450183 × 10 ⁻¹² /с

dψ _L /dt = 5,334529 × 10 ⁻¹² /с

оба из них должны быть преобразованы в ″/a (угловые секунды/год) по количеству угловых секунд в 2 π радианах (1,296 × 10 ⁶ ″/2π) и количество секунд в одном году ( юлианский год ) (3,15576 × 10 ⁷ с/а):

dψ _S /dt = 15,948788″/год против 15,948870″/год у Уильямса

dψ _L /dt = 34,723638″/год против 34,457698″/год у Уильямса.

Солнечное уравнение является хорошим представлением прецессии Солнца, поскольку орбита Земли близка к эллипсу и лишь незначительно возмущается другими планетами. Лунное уравнение не так хорошо отражает прецессию Луны, поскольку орбита Луны сильно искажена Солнцем, и ни радиус, ни эксцентриситет не являются постоянными в течение года.

Ценности

Расчеты Саймона Ньюкомба в конце 19-го века для общей прецессии ( p ) по долготе дали значение 5025,64 угловых секунды за тропический век и были общепринятым значением до тех пор, пока искусственные спутники не обеспечили более точные наблюдения, а электронные компьютеры не позволили создать более сложные модели. быть рассчитано. Джей Генри Лиске разработал обновленную теорию в 1976 году, где p равно 5 029,0966 угловых секунд (или 1,3969713 градусов) на юлианское столетие. Современные методы, такие как РСДБ и LLR, позволили провести дальнейшие усовершенствования, и Международный астрономический союз принял новое постоянное значение в 2000 году, а также новые методы вычислений и полиномиальные выражения в 2003 и 2006 годах; накопленная прецессия равна :

р _А = 5028,796195 Т + 1,1054348 Т ² + члены более высокого порядка, в угловых секундах, с T , временем в юлианских столетиях (то есть 36 525 дней) с эпохи 2000 года .

Скорость прецессии является производной от этого:

p = 5,028,796195 + 2,2108696 T + члены более высокого порядка.

Постоянный член этой скорости (5 028,796195 угловых секунд на столетие в приведенном выше уравнении) соответствует одному полному кругу прецессии за 25 771,57534 года (один полный круг в 360 градусов, разделенный на 50,28796195 угловых секунд в год). хотя некоторые другие источники оценивают это значение в 25771,4 года, что оставляет небольшую неопределенность.

Скорость прецессии не является постоянной величиной, но (на данный момент) медленно увеличивается с течением времени, на что указывают линейные члены (и более высокого порядка) в T . В любом случае следует подчеркнуть, что эта формула действительна только в течение ограниченного периода времени . Это полиномиальное выражение, основанное на данных J2000, эмпирически подобранное к данным наблюдений, а не к детерминистской модели Солнечной системы . Ясно, что если T станет достаточно большим (далеко в будущем или далеко в прошлом), член T² будет доминировать, и p достигнет очень больших значений. В действительности, более сложные расчеты численной модели Солнечной системы показывают, что скорость прецессии имеет период около 41 000 лет, такой же, как и наклон эклиптики. То есть,

р = А + БТ + КТ ² + …

является приближением

p = a + b sin (2π T / P ), где P — период в 41 000 лет.

Теоретические модели могут рассчитывать константы (коэффициенты), соответствующие высшим степеням T , но поскольку полином не может соответствовать периодической функции по всем числам, разница во всех таких приближениях будет неограниченно расти по мере T. увеличения Достаточная точность может быть получена за ограниченный промежуток времени путем подбора полинома достаточно высокого порядка к данным наблюдений, а не обязательно несовершенной динамической численной модели. Для современных расчетов траекторий полета искусственных спутников и космических аппаратов большую точность дает полиномиальный метод. В этом отношении Международный астрономический союз выбрал наиболее развитую из имеющихся теорий. На протяжении нескольких столетий в прошлом и будущем ни одна из используемых формул не сильно расходилась. Большинство согласны с некоторой точностью на период до нескольких тысяч лет в прошлом и будущем. Для более поздних эпох расхождения становятся слишком большими – точную скорость и период прецессии невозможно вычислить с использованием этих полиномов даже для одного целого периода прецессии.

Прецессия земной оси — очень медленный эффект, но при том уровне точности, с которым работают астрономы, его необходимо принимать во внимание ежедневно. Хотя прецессия и наклон оси Земли (наклон эклиптики) рассчитываются по одной и той же теории и, таким образом, связаны друг с другом, эти два движения действуют независимо друг от друга, двигаясь в противоположных направлениях.

Скорость прецессии демонстрирует вековое снижение из-за приливной диссипации с 59 дюймов/год до 45 дюймов/год (а = год = юлианский год ) в течение периода в 500 миллионов лет, сосредоточенного в настоящее время. После усреднения краткосрочных колебаний (десятки тысяч лет) долгосрочный тренд можно аппроксимировать следующими полиномами для отрицательного и положительного времени от настоящего в "/а, где Т - в миллиардах юлианских лет ( Га):

п ⁻ = 50,475838 − 26,368583 Т + 21,890862 Т ²

п ⁺ = 50,475838 − 27,000654 Т + 15,603265 Т ²

Это дает среднюю продолжительность цикла в настоящее время 25 676 лет.

Прецессия будет больше p ⁺ на небольшую величину +0,135052"/а между +30 и +130 млн лет . Скачок к этому превышению над p ⁺ произойдет всего через 20 млн лет назад, потому что вековое уменьшение прецессии начинает пересекать резонанс на орбите Земли, вызванный другими планетами.

По мнению У. Р. Уорда, примерно через 1500 миллионов лет, когда расстояние до Луны, постоянно увеличивающееся из-за приливных эффектов, увеличится с нынешних 60,3 до примерно 66,5 земных радиусов, резонансы от планетарных эффектов сначала подтолкнут прецессию к 49 000 лет. , а затем, когда Луна достигнет 68 земных радиусов примерно за 2000 миллионов лет, до 69000 лет. Это будет связано и с резкими колебаниями наклона эклиптики. Уорд, однако, использовал аномально большое современное значение приливной диссипации. Если использовать среднюю продолжительность жизни в 620 миллионов лет, обеспечиваемую приливными ритмитами, составляющими примерно половину современного значения, эти резонансы не будут достигнуты примерно через 3000 и 4000 миллионов лет соответственно. Однако из-за постепенно увеличивающейся светимости Солнца океаны Земли испарится до этого времени (примерно через 2100 миллионов лет).

См. также

• Астрономическая нутация
• Осевой наклон
• углы Эйлера
• Долгота весеннего равноденствия
• Циклы Миланковича
• Полярное движение
• Звездный год
• Апсидальная прецессия

Ссылки

Библиография

• Бергер, Ал. (1976). «Наклон и прецессия за последние 5000000 лет». Астрономия и астрофизика . 51 (1): 127–135. Бибкод : 1976A&A....51..127B .
• Капитан, Н. (2003). «Выражения для величин прецессии IAU 2000» . Астрономия и астрофизика . 412 (2): 567–586. Бибкод : 2003A&A...412..567C . дои : 10.1051/0004-6361:20031539 .
• Дрейер, Дж.Л.Е. История астрономии от Фалеса до Кеплера . 2-е изд. Нью-Йорк: Дувр, 1953.
• Эванс, Джеймс. История и практика древней астрономии . Нью-Йорк: Издательство Оксфордского университета, 1998.
• Пояснительное приложение к Астрономическим эфемеридам и Американским эфемеридам и Морскому альманаху.
• Хилтон, Дж.Л. (2006). «Отчет Рабочей группы Отдела I Международного астрономического союза по прецессии и эклиптике» (PDF) . Небесная механика и динамическая астрономия . 94 (3): 351–367. Бибкод : 2006CeMDA..94..351H . дои : 10.1007/s10569-006-0001-2 . S2CID   122358401 .
• Лиске, Дж. Х.; Ледерле, Т.; Фрике, В. (1977). «Выражения для величин прецессии на основе системы астрономических констант МАС (1976)». Астрон. Астрофизика . 58 : 1–16. Бибкод : 1977A&A....58....1L .
• Прецессия и наклон эклиптики сравниваются значения, предсказанные различными теориями.
• Паннекук, А. История астрономии . Нью-Йорк: Дувр, 1961.
• Паркер, Ричард А. «Египетская астрономия, астрология и календарный счисление». Словарь научной биографии 15:706–727.
• Райс, Майкл (1997), Наследие Египта: архетипы западной цивилизации, 3000–30 гг. До н.э. , Лондон и Нью-Йорк.
• Шютц, Майкл (2000). «Гиппарх и открытие прецессии. Заметки о Дэвиде Уланси, «Происхождение культа Митры» . Электронный журнал митраистических исследований (на немецком языке). 1 . Архивировано из оригинала 4 ноября 2013 года.
• Саймон, Дж.Л. (1994). «Численные выражения для формул прецессии и средних элементов для Луны и планет». Астрономия и астрофизика . 282 : 663–683. Бибкод : 1994A&A...282..663S .
• Томпкинс, Питер . Тайны Великой пирамиды . С приложением Ливио Катулло Стеккини. Нью-Йорк: Книги Харпера Колофона, 1971.
• Тумер, Г.Дж. «Гиппарх». Словарь научной биографии . Том. 15:207–224. Нью-Йорк: Сыновья Чарльза Скрибнера, 1978.
• Тумер, Альмагест Г. Дж. Птолемея . Лондон: Дакворт, 1984.
• Уланси, Дэвид. Истоки митраистских мистерий: космология и спасение в древнем мире . Нью-Йорк: Издательство Оксфордского университета, 1989.
• Вондрак, Дж.; Капитан, Н.; Уоллес, П. (2011). «Новые выражения прецессии, действительные для больших интервалов времени» . Астрономия и астрофизика . 534 : А22. Бибкод : 2011A&A...534A..22V . дои : 10.1051/0004-6361/201117274 .

Внешние ссылки

• Дебаты Даламбера и Эйлера о решении проблемы прецессии равноденствий
• Боули, Роджер; Меррифилд, Майкл. «Осевая прецессия» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .
• Вынужденная прецессия и нутация Земли.