Овал

Овал , (от лат. ovum «яйцо») — это замкнутая кривая в плоскости напоминающая очертания яйца . Термин не очень конкретен, но в некоторых областях ( проективная геометрия , техническое черчение и т. д.) ему дается более точное определение, которое может включать как одну, так и две оси симметрии эллипса . В обычном английском языке этот термин используется в более широком смысле: любая форма, напоминающая яйцо. Трехмерная версия овала называется овоидом .

Овал в геометрии

Этот овал, имеющий только одну ось симметрии, напоминает куриное яйцо.

Термин «овал» , используемый для описания кривых в геометрии, не имеет четкого определения, за исключением контекста проективной геометрии . Многие отчетливые кривые обычно называют овалами или имеют «овальную форму». Обычно, чтобы называться овалом, плоская кривая должна напоминать очертание яйца или эллипса . В частности, это общие черты овалов:

они дифференцируемы (гладкие), ^[1] простые (не самопересекающиеся), выпуклые , замкнутые , плоские кривые ;
их форма не сильно отличается от формы эллипса , и
овал обычно имеет ось симметрии , но это не обязательно.

Вот примеры овалов, описанных в другом месте:

Овоид — это поверхность в трехмерном пространстве, образованная вращением овальной кривой вокруг одной из ее осей симметрии.Прилагательные овоидный и яйцевидный означают наличие яйцевидной формы и часто используются как синонимы слова «яйцевидный».

Проективная геометрия

К определению овала в проективной плоскости

На проективной плоскости множество $точек Ω$ называется овалом , если:

Любая прямая $l$ пересекает $Ω$ не более чем в двух точках, и
Для любой точки $P \in Ω$ существует ровно одна касательная $t,$ проходящая через $P$ , т. е. $t \cap Ω = {P$ }.

Для конечных плоскостей (т. е. множество точек конечно) существует более удобная характеристика: ^[2]

Для конечной проективной плоскости порядка $n$ (т.е. любая прямая содержит $n + 1$ точку) множество $точек Ω$ является овалом тогда и только тогда, когда $| Ом | = n + 1$ и никакие три точки не лежат на одной прямой.

Овоид точек в проективном пространстве — это множество $:$ Ω такое, что

Любая прямая пересекает $Ω$ не более чем в 2 точках,
Касательные в точке покрывают гиперплоскость (и не более того), а
$Ω$ не содержит линий.

В конечном случае только для размерности 3 существуют овоиды. Удобная характеристика:

В 3-х разм. конечное проективное пространство порядка $n > 2,$ любое множество точек $Ω$ является овоидом тогда и только тогда, когда | $Ом$ | $=n^{2}+1$ и никакие три точки не лежат на одной прямой. ^[3]

Форма яйца

Форма яйца аппроксимируется «длинной» половиной вытянутого сфероида , соединенной с «короткой» половиной примерно сферического эллипсоида или даже слегка сплюснутого сфероида . Они соединены на экваторе и имеют общую главную ось вращательной симметрии , как показано выше. Хотя термин «яйцеобразная» обычно подразумевает отсутствие симметрии отражения в экваториальной плоскости, он также может относиться к истинным вытянутым эллипсоидам. Его также можно использовать для описания двухмерной фигуры, которая, если вращаться вокруг своей главной оси , создает трехмерную поверхность.

Технический чертеж

В техническом рисунке овал — это фигура, состоящая из двух пар дуг с двумя разными радиусами (см. изображение справа). Дуги соединяются в точке, в которой линии, касательные к обеим соединяемым дугам, лежат на одной линии, что делает соединение гладким. Любая точка овала принадлежит дуге постоянного радиуса (более или более длинного), а вот у эллипса радиус постоянно меняется.

В просторечии

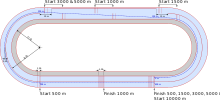
В просторечии «овал» означает форму, похожую на яйцо или эллипс, которая может быть двухмерной или трехмерной. Это также часто относится к фигуре, напоминающей два полукруга, соединенных прямоугольником, например, поле для крикета , каток или легкоатлетическую дорожку . Однако правильнее всего это назвать стадионом .

Термин «эллипс» часто используется как синоним слова «овал», хотя он не является точным синонимом. ^[4] Термин «продолговатый» часто используется неправильно для описания удлиненного овала или формы стадиона. ^[5] Однако в геометрии продолговатый прямоугольник — это прямоугольник с неравными прилегающими сторонами (т. е. не квадрат). ^[6]

См. также

Примечания

^ Если свойство имеет смысл: на дифференцируемом многообразии. В более общих настройках может потребоваться только уникальная касательная линия в каждой точке кривой.
^ Дембовский 1968 , с. 147
^ Дембовский 1968 , с. 48
^ «Определение эллипса в американском английском согласно Оксфордским словарям» . Новый Оксфордский американский словарь . Издательство Оксфордского университета. Архивировано из оригинала 27 сентября 2016 года . Проверено 9 июля 2018 г.
^ «Определение продолговатого слова в американском английском согласно Оксфордским словарям» . Новый Оксфордский американский словарь . Издательство Оксфордского университета. Архивировано из оригинала 24 сентября 2016 года . Проверено 9 июля 2018 г.
^ «Определение четырехугольников, Университет Кларка, факультет математики и информатики» . Университет Кларка, Определения четырехугольников . Проверено 21 октября 2020 г.

Дембовский, Питер (1968), Конечная геометрия , результаты математики и ее пограничные области , Том 44, Берлин, Нью-Йорк: Springer-Verlag , ISBN 3-540-61786-8 , МР 0233275

[1] Если свойство имеет смысл: на дифференцируемом многообразии. В более общих настройках может потребоваться только уникальная касательная линия в каждой точке кривой.

[2] Дембовский 1968 , с. 147

[3] Дембовский 1968 , с. 48

[4] «Определение эллипса в американском английском согласно Оксфордским словарям» . Новый Оксфордский американский словарь . Издательство Оксфордского университета. Архивировано из оригинала 27 сентября 2016 года . Проверено 9 июля 2018 г.

[5] «Определение продолговатого слова в американском английском согласно Оксфордским словарям» . Новый Оксфордский американский словарь . Издательство Оксфордского университета. Архивировано из оригинала 24 сентября 2016 года . Проверено 9 июля 2018 г.

[6] «Определение четырехугольников, Университет Кларка, факультет математики и информатики» . Университет Кларка, Определения четырехугольников . Проверено 21 октября 2020 г.

[1]

[2]

[3]

[4]

[5]

[6]