Двухпортовая сеть

В электронике двухполюсная сеть (разновидность четырехполюсной сети или четырехполюсника ) — это сеть (т.е. цепь) или устройство с двумя парами клемм электрическая для подключения к внешним цепям. Две клеммы составляют порт, если приложенные к ним токи удовлетворяют основному требованию, известному как условие порта: ток, входящий в одну клемму, должен быть равен току, выходящему из другой клеммы того же порта. [1] [2] Порты представляют собой интерфейсы, через которые сеть соединяется с другими сетями, точки, где подаются сигналы или принимаются выходные данные. В сети с двумя портами часто порт 1 считается входным портом, а порт 2 — выходным портом.
Он обычно используется в математическом анализе цепей .
Приложение
[ редактировать ]Модель двухпортовой сети используется в методах математического анализа цепей для изоляции частей более крупных цепей. Двухпортовая сеть рассматривается как « черный ящик », свойства которого задаются матрицей чисел . Это позволяет легко рассчитать реакцию сети на сигналы, подаваемые на порты, без учета всех внутренних напряжений и токов в сети. Это также позволяет легко сравнивать аналогичные схемы или устройства. Например, транзисторы часто рассматривают как двухпортовые, характеризующиеся h -параметрами (см. ниже), указанными производителем. Любую линейную цепь с четырьмя выводами можно рассматривать как двухполюсную сеть при условии, что она не содержит независимого источника и удовлетворяет условиям порта.
Примерами схем, анализируемых как двухпортовые, являются фильтры , согласующие сети , линии передачи , трансформаторы и модели малых сигналов для транзисторов (такие как модель гибридного пи ). Анализ пассивных двухпортовых сетей является результатом теорем взаимности, впервые выведенных Лоренцем. [3]
В двухпортовых математических моделях сеть описывается квадратной матрицей комплексных чисел размером 2 на 2 . Общие используемые модели называются z - параметрами , y - параметрами , h - параметрами , g - параметрами и ABCD - параметрами , каждый из которых описан отдельно ниже. Все они ограничены линейными сетями, поскольку в основе их вывода лежит то, что любое данное состояние цепи представляет собой линейную суперпозицию различных состояний короткого замыкания и разомкнутой цепи. Обычно они выражаются в матричной записи и устанавливают связи между переменными
- В 1 , напряжение на порту 1
- I 1 , ток в порт 1
- В 2 , напряжение на порте 2
- I 2 , ток в порт 2
которые показаны на рисунке 1. Разница между различными моделями заключается в том, какие из этих переменных считаются независимыми переменными . Эти переменные тока и напряжения наиболее полезны на низких и средних частотах. На высоких частотах (например, микроволновых частотах) использование переменных мощности и энергии более целесообразно, а двухпортовый подход ток-напряжение заменяется подходом, основанным на параметрах рассеяния .
Общие свойства
[ редактировать ]Существуют определенные свойства двухпортов, которые часто встречаются в практических сетях и могут быть использованы для значительного упрощения анализа. К ним относятся:
- Взаимные сети
- Сеть называется взаимной, если напряжение, возникающее на порту 2 из-за тока, приложенного к порту 1, такое же, как напряжение, возникающее на порту 1, когда тот же ток подается на порт 2. Обмен напряжением и током приводит к эквивалентному результату. определение взаимности. Сеть, полностью состоящая из линейных пассивных компонентов (то есть резисторов, конденсаторов и катушек индуктивности), обычно является взаимной, за исключением пассивных циркуляторов и изоляторов , содержащих намагниченные материалы. В общем, не будет взаимности, если он будет содержать активные компоненты, такие как генераторы или транзисторы. [4]
- Симметричные сети
- Сеть считается симметричной, если ее входное сопротивление равно выходному сопротивлению. Чаще всего, но не обязательно, симметричные сети также являются физически симметричными. Иногда и антиметрические сети представляют интерес . Это сети, в которых входное и выходное сопротивление двойственно друг другу. [5]
- Сеть без потерь
- Сеть без потерь — это сеть, которая не содержит резисторов или других рассеивающих элементов. [6]
Параметры импеданса ( z -параметры)
[ редактировать ]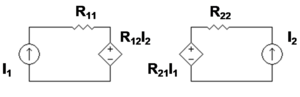
где
Все z -параметры имеют размерность в омах .
Для взаимных сетей z 12 = z 21 . Для симметричных сетей z 11 = z 22 . Для взаимных сетей без потерь все z mn чисто мнимые. [7]
Пример: биполярное токовое зеркало с вырождением эмиттера.
[ редактировать ]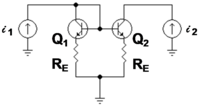

На рис. 3 показано биполярное токовое зеркало с эмиттерными резисторами для увеличения его выходного сопротивления. [номер 1] Транзистор Q 1 подключен диодом , то есть его напряжение коллектор-база равно нулю. На рисунке 4 показана схема слабого сигнала, эквивалентная рисунку 3. Транзистор Q 1 представлен сопротивлением его эмиттера r E :
упрощение стало возможным, поскольку зависимый источник тока в модели гибридного пи для Q 1 потребляет тот же ток, что и резистор 1 / g m, подключенный к резистору r π . Второй транзистор Q 2 представлен своей гибридной пи-моделью . В таблице 1 ниже показаны выражения z-параметров, которые делают z-эквивалентную схему на рисунке 2 электрически эквивалентной слабосигнальной схеме на рисунке 4.
| Выражение | Приближение | |
|---|---|---|
| [номер 2] | ||
отрицательную обратную связь, вносимую резисторами R E. В этих параметрах можно увидеть Например, при использовании в качестве активной нагрузки в дифференциальном усилителе I 1 ≈ − I 2 , что делает выходное сопротивление зеркала примерно
по сравнению только с r O без обратной связи (то есть с R E = 0 Ом). При этом импеданс на опорной стороне зеркала примерно равен
лишь умеренное значение, но все же больше, чем r E, без обратной связи. В применении дифференциального усилителя большое выходное сопротивление увеличивает коэффициент усиления разностного режима, что хорошо, а небольшое входное сопротивление зеркала желательно, чтобы избежать эффекта Миллера .
Параметры адмиттанса ( y -параметры)
[ редактировать ]
где
Все Y -параметры имеют размерность в сименсах .
Для взаимных сетей y 12 = y 21 . Для симметричных сетей y 11 = y 22 . Для взаимных сетей без потерь все эти значения являются чисто мнимыми. [7]
Гибридные параметры ( h -параметры)
[ редактировать ]
где
Эту схему часто выбирают, когда на выходе требуется усилитель тока. Вместо этого резисторы, показанные на схеме, могут быть общими импедансами.
Внедиагональные h -параметры безразмерны , а диагональные элементы имеют размеры, обратные друг другу.
Для взаимных сетей h 12 = – h 21 . Для симметричных сетей h 11 h 22 – h 12 h 21 = 1 . Для взаимных сетей без потерь h 12 и h 21 действительны, тогда как h 11 и h 22 являются чисто мнимыми.
Пример: усилитель с общей базой
[ редактировать ]
Примечание. Табличные формулы в таблице 2 приводят h- эквивалентную схему транзистора на рисунке 6 в соответствие с его малосигнальной низкочастотной гибридной пи-моделью на рисунке 7. Обозначения: r π — сопротивление базы транзистора, r O — выходное сопротивление. сопротивление, g m – взаимная крутизна. Отрицательный знак для h 21 отражает соглашение о том, что I 1 , I 2 положительны, когда направлены в двухпортовый порт. Ненулевое значение h 12 означает, что выходное напряжение влияет на входное напряжение, то есть этот усилитель является двусторонним . Если h 12 = 0 , усилитель односторонний .
| Выражение | Приближение | |
|---|---|---|
История
[ редактировать ]- параметры h первоначально назывались последовательно-параллельными параметрами . Термин «гибрид» для описания этих параметров был введен Д. А. Альсбергом в 1953 г. в книге «Транзисторная метрология». [8] В 1954 году совместный комитет IRE и AIEE принял термин h - параметры и рекомендовал, чтобы они стали стандартным методом тестирования и определения характеристик транзисторов, поскольку они «особенно адаптируются к физическим характеристикам транзисторов». [9] В 1956 году рекомендация стала стандартом; 56 ИРЭ 28.С2. После слияния этих двух организаций в IEEE стандарт стал Std 218-1956 и был подтвержден в 1980 году, но сейчас отозван. [10]
Обратные гибридные параметры (g-параметры)
[ редактировать ]
где
Часто эту схему выбирают, когда на выходе требуется усилитель напряжения. Внедиагональные g-параметры безразмерны, в то время как диагональные элементы имеют размеры, обратные друг другу. Вместо этого резисторы, показанные на схеме, могут быть общими импедансами.
Пример: усилитель с общей базой
[ редактировать ]
Примечание. Табличные формулы в таблице 3 приводят g- эквивалентную схему транзистора на рисунке 8 в соответствие с его малосигнальной низкочастотной гибридной пи-моделью на рисунке 9. Обозначения: r π — сопротивление базы транзистора, r O — выходное сопротивление. сопротивление, g m – взаимная крутизна. Отрицательный знак для g 12 отражает соглашение о том, что I 1 , I 2 являются положительными, когда направлены в двухпортовый порт. Ненулевое значение g 12 означает, что выходной ток влияет на входной ток, то есть этот усилитель двусторонний . Если g 12 = 0 , усилитель односторонний .
| Выражение | Приближение | |
|---|---|---|
ABCD -параметры
[ редактировать ]Параметры ABCD известны под разными названиями: параметры цепочки, каскада или передачи. Существует несколько определений параметров ABCD , наиболее распространенным является: [11] [12]
Примечание. Некоторые авторы решили изменить указанное направление I 2 на противоположное и подавить отрицательный знак I 2 .
где
Для взаимных сетей AD – BC = 1 . симметричных сетей A = D. Для Для сетей, которые являются взаимными и без потерь, A и D являются чисто реальными, а B и C — чисто воображаемыми. [6]
Такое представление является предпочтительным, поскольку когда параметры используются для представления каскада из двух портов, матрицы записываются в том же порядке, в котором будет рисоваться сетевая диаграмма, то есть слева направо. Однако используется и вариант определения: [13]
где
Отрицательный знак – I 2 возникает для того, чтобы выходной ток одного каскадного каскада (как он указан в матрице) равен входному току следующего. Без знака минус два тока имели бы противоположные направления, поскольку положительное направление тока по соглашению считается током, поступающим в порт. Следовательно, вектор входной матрицы напряжения/тока можно напрямую заменить матричным уравнением предыдущего каскадного каскада для формирования объединенной матрицы A'B'C'D' .
Терминология представления параметров ABCD в виде матрицы элементов, обозначаемых цифрой 11 и т. д., принятая некоторыми авторами. [14] а обратные параметры A'B'C'D' в виде матрицы элементов, обозначенных b 11 и т. д., используются здесь как для краткости, так и во избежание путаницы с элементами схемы.
Таблица параметров передачи
[ редактировать ]В таблице ниже перечислены параметры ABCD и обратные параметры ABCD для некоторых простых элементов сети.
| Элемент | [ а ] матрица | [ б ] матрица | Примечания |
|---|---|---|---|
| Последовательный импеданс | Z , импеданс | ||
| Вход шунта | Ю , прием | ||
| Серийный индуктор | L , индуктивность s , комплексная угловая частота | ||
| Шунтирующий индуктор | L , индуктивность s , комплексная угловая частота | ||
| Последовательный конденсатор | С , емкость s , комплексная угловая частота | ||
| Шунтирующий конденсатор | С , емкость s , комплексная угловая частота | ||
| Линия передачи | [15] | Z 0 , волновое сопротивление γ , постоянная распространения ( ) l , длина линии электропередачи ( м ) |
Параметры рассеяния (S-параметры)
[ редактировать ]
Все предыдущие параметры определяются напряжениями и токами на портах. S -параметры различны и определяются с точки зрения падающих и отраженных волн в портах. S -параметры используются в основном на частотах УВЧ и СВЧ , где становится затруднительным непосредственное измерение напряжения и тока. С другой стороны, падающую и отраженную мощность легко измерить с помощью направленных ответвителей . Определение таково: [16]
где a k — падающие волны, а b k — отраженные волны в порту k . Традиционно a k и b k определяют в терминах квадратного корня из степени. Следовательно, существует связь с волновыми напряжениями (подробнее см. В основной статье). [17]
Для взаимных сетей S 12 = S 21 . Для симметричных сетей S 11 = S 22 . Для антиметрических сетей S 11 = – S 22 . [18] Для взаимных сетей без потерь и [19]
Рассеяние параметров переноса ( Т -параметры)
[ редактировать ]Параметры переноса рассеяния, как и параметры рассеяния, определяются через падающие и отраженные волны. Разница в том, что T -параметры связывают волны в порту 1 с волнами в порту 2, тогда как S -параметры связывают отраженные волны с падающими волнами. В этом отношении T -параметры выполняют ту же роль, что и параметры ABCD , и позволяют T вычислять -параметры каскадных сетей путем матричного умножения составляющих сетей. Т -параметры, как и параметры ABCD , также можно назвать параметрами передачи. Определение таково: [16] [20]
Т -параметры не так легко измерить напрямую, как S -параметры. Однако S -параметры легко конвертируются в T -параметры, подробности см. в основной статье. [21]
Комбинации двухпортовых сетей
[ редактировать ]При соединении двух и более двухполюсников двухполюсные параметры объединенной сети можно найти путем выполнения матричной алгебры над матрицами параметров составляющих двухполюсников. Работу матрицы можно сделать особенно простой за счет соответствующего выбора двухпортовых параметров, соответствующих форме соединения двух портов. Например, z -параметры лучше всего подходят для последовательно соединенных портов.
Правила комбинирования следует применять с осторожностью. Некоторые соединения (когда соединяются разнородные потенциалы) приводят к тому, что состояние порта становится недействительным и правило комбинирования больше не применяется. тест Брюна Для проверки допустимости комбинации можно использовать . Эту трудность можно преодолеть, разместив на выходах проблемного двухполюсника идеальные трансформаторы 1:1. Это не меняет параметры двух портов, но гарантирует, что они будут продолжать соответствовать условиям порта при соединении между собой. Пример этой проблемы показан для последовательно-последовательных соединений на рисунках 11 и 12 ниже. [22]
Последовательное соединение
[ редактировать ]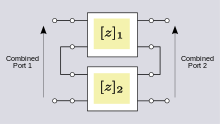
Когда два порта соединены в последовательно-последовательной конфигурации, как показано на рисунке 10, лучшим выбором двухпортового параметра являются z -параметры. - параметры Z объединенной сети находятся путем сложения двух отдельных матриц z -параметров. [23] [24]

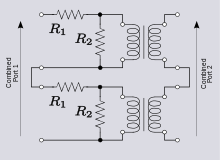
Как упоминалось выше, существуют сети, которые не поддаются непосредственному анализу. [22] Простой пример — двухполюсник, состоящий из L -цепи резисторов R 1 и R 2 . - параметры Z для этой сети:
На рисунке 11 показаны две одинаковые такие сети, соединенные последовательно-последовательно. Общие z -параметры, предсказанные сложением матрицы, составляют;
Однако непосредственный анализ комбинированной схемы показывает, что
Несоответствие объясняется тем, что R 1 нижнего двухпортового резистора был зашунтирован из-за короткого замыкания между двумя клеммами выходных портов. Это приводит к тому, что ток не протекает через одну клемму в каждом из входных портов двух отдельных сетей. Следовательно, состояние порта нарушается для обоих входных портов исходной сети, поскольку ток все еще может течь в другой терминал. Эту проблему можно решить, вставив идеальный трансформатор в выходной порт хотя бы одной из двухполюсников. Хотя это стандартный подход к изложению теории двухпортовых устройств, практичность использования трансформаторов является вопросом, который необходимо решать для каждой отдельной конструкции.
Параллельно-параллельное соединение
[ редактировать ]
Когда два порта соединены в параллельно-параллельной конфигурации, как показано на рисунке 13, лучшим выбором двухпортового параметра являются y -параметры. - параметры Y объединенной сети находятся путем сложения двух отдельных матриц y -параметров. [25]
Последовательно-параллельное соединение
[ редактировать ]
Когда два порта соединены последовательно-параллельно, как показано на рисунке 14, лучшим выбором двухпортового параметра являются h -параметры. - параметры h объединенной сети находятся путем сложения двух отдельных матриц h -параметров. [26]
Параллельно-последовательное соединение
[ редактировать ]
Когда два порта соединены в параллельно-последовательной конфигурации, как показано на рисунке 15, лучшим выбором двухпортового параметра являются g -параметры. - параметры g объединенной сети находятся путем сложения двух отдельных матриц g -параметров.
Каскадное подключение
[ редактировать ]
Когда два порта соединены так, что выходной порт первого подключен к входному порту второго (каскадное соединение), как показано на рисунке 16, лучшим выбором двухпортового параметра являются параметры ABCD . -параметры объединенной сети находятся путем матричного умножения двух отдельных матриц a -параметров. [27]
Цепочку из n двухпортов можно объединить матричным умножением n матриц. Для объединения каскада матриц b -параметров их снова перемножают, но умножение необходимо производить в обратном порядке, так что;
Пример
[ редактировать ]у нас есть двухпортовая сеть, состоящая из последовательного резистора R, за которым следует шунтирующий конденсатор C. Предположим , Мы можем смоделировать всю сеть как каскад двух более простых сетей:
Матрица передачи для всей сети [ b ] — это просто матричное умножение матриц передачи для двух элементов сети:
Таким образом:
Взаимосвязь параметров
[ редактировать ]| [ С ] | [ и ] | [ ч ] | [ г ] | [ а ] | [ б ] | |
|---|---|---|---|---|---|---|
| [ С ] | ||||||
| [ и ] | ||||||
| [ ч ] | ||||||
| [ г ] | ||||||
| [ а ] | ||||||
| [ б ] |
Где [ x ] является определителем x [ ] . Δ
Некоторые пары матриц имеют особенно простые отношения. Параметры проводимости представляют собой обратную матрицу параметров импеданса, обратные гибридные параметры представляют собой обратную матрицу гибридных параметров, а [ b ] форма ABCD -параметров является матрицей, обратной форме [ a ] . То есть,
Сети с более чем двумя портами
[ редактировать ]Хотя сети с двумя портами очень распространены (например, усилители и фильтры), другие электрические сети, такие как направленные ответвители и циркуляторы, имеют более двух портов. Следующие представления также применимы к сетям с произвольным количеством портов:
Например, параметры импеданса трех портов приводят к следующей зависимости:
Однако следующие представления обязательно ограничиваются двухпортовыми устройствами:
- Гибридные ( h ) параметры
- обратного гибрида ( g ) Параметры
- передачи ( ABCD ) Параметры
- переноса рассеяния ( T ) Параметры
Свертывание двухпортового в один порт
[ редактировать ]Двухпортовая сеть имеет четыре переменные, две из которых независимы. Если один из портов завершается нагрузкой без независимых источников, то нагрузка обеспечивает связь между напряжением и током этого порта. Часть свободы теряется. Теперь схема имеет только один независимый параметр. Двухпортовый импеданс становится однопортовым по отношению к оставшейся независимой переменной.
Например, рассмотрим параметры импеданса
Подключение нагрузки Z L к порту 2 фактически добавляет ограничение.
Отрицательный знак обусловлен тем, что положительное направление I 2 направлено в двухполюсник, а не в нагрузку. Расширенные уравнения принимают вид
Второе уравнение можно легко решить для I 2 как функции I 1 и это выражение может заменить I 2 в первом уравнении, оставив V 1 (и V 2 и I 2 ) как функции I 1
Таким образом, по сути, I 1 видит входное сопротивление Z in , и влияние двухпортового режима на входную цепь фактически сводится к однопортовому; т. е. простой двухполюсный импеданс.
См. также
[ редактировать ]- Параметры допуска
- Параметры импеданса
- Параметры рассеяния
- Трансфер-матричный метод (оптика) для расчета отражения/пропускания световых волн в прозрачных слоях
- Матрица лучевого переноса для расчета параксиального распространения светового луча
Примечания
[ редактировать ]- ^ Резисторы эмиттерной ветви противодействуют любому увеличению тока, уменьшая напряжение транзистора V BE . То есть резисторы R E вызывают отрицательную обратную связь, препятствующую изменению тока. В частности, любое изменение выходного напряжения приводит к меньшему изменению тока, чем без этой обратной связи, что означает, что выходное сопротивление зеркала увеличилось.
- ^ Двойная вертикальная черта обозначает параллельное соединение резисторов: .
Ссылки
[ редактировать ]- ^ Грей, §3.2, с. 172
- ^ Джагер, §10.5 §13.5 §13.8
- ^ Джаспер Дж. Гудблуд. «Измерения взаимности и ЭМС» (PDF) . ЭМСС . Проверено 28 апреля 2014 г.
- ^ Нахви, стр. 311.
- ^ Мэтью и др., стр. 70–72.
- ^ Jump up to: а б Мэтью и др., с. 27.
- ^ Jump up to: а б Мэтью и др., с. 29.
- ^ 56 IRE 28.S2, с. 1543 г.
- ^ Отчет комитета AIEE-IRE, стр. 725
- ^ Стандарт IEEE 218-1956.
- ^ Мэтью и др., стр. 26.
- ^ Гош, с. 353.
- ^ А. Чакрабарти, с. 581, ISBN 81-7700-000-4 , Dhanpat Rai & Co pvt. ООО
- ^ Фараго, стр. 102.
- ^ Клейтон, с. 271.
- ^ Jump up to: а б Василеска и Гудник, стр. 137.
- ^ Иган, стр. 11–12.
- ^ Карлин, с. 304
- ^ Мэтью и др., стр. 44
- ^ Иган, стр. 12–15.
- ^ Иган, стр. 13–14.
- ^ Jump up to: а б Фараго, стр. 122–127.
- ^ Гош, с. 371.
- ^ Фараго, стр. 128.
- ^ Гош, с. 372.
- ^ Гош, с. 373.
- ^ Фараго, стр. 128–134.
Библиография
[ редактировать ]- Карлин, Х.Дж., Чиваллери, П.П., Проектирование широкополосной схемы , CRC Press, 1998. ISBN 0-8493-7897-4 .
- Уильям Ф. Иган, Практическое проектирование радиочастотных систем , Wiley-IEEE, 2003 г. ISBN 0-471-20023-9 .
- Фараго, П.С., Введение в линейный сетевой анализ , The English Universities Press Ltd, 1961.
- Грей, PR; Херст, П.Дж.; Льюис, Ш.; Мейер, Р.Г. (2001). Анализ и проектирование аналоговых интегральных схем (4-е изд.). Нью-Йорк: Уайли. ISBN 0-471-32168-0 .
- Гош, Смараджит, Теория сетей: анализ и синтез , Прентис Холл, Индия ISBN 81-203-2638-5 .
- Джагер, RC; Блэлок, Теннесси (2006). Проектирование микроэлектронных схем (3-е изд.). Бостон: МакГроу-Хилл. ISBN 978-0-07-319163-8 .
- Маттеи, Янг, Джонс, Микроволновые фильтры, сети согласования импедансов и структуры связи , McGraw-Hill, 1964.
- Махмуд Нахви, Джозеф Эдминистрист, Очерк теории и проблем электрических цепей Шаума , McGraw-Hill Professional, 2002 г. ISBN 0-07-139307-2 .
- Драгица Василеска , Стивен Маршалл Гудник, Вычислительная электроника , Morgan & Claypool Publishers, 2006 г. ISBN 1-59829-056-8 .
- Клейтон Р. Пол, Анализ многопроводных линий передачи , John Wiley & Sons, 2008 г. ISBN 0470131543 , 9780470131541.
история h-параметров
[ редактировать ]- Д. А. Альсберг, «Транзисторная метрология», Протокол конвенции IRE , часть 9, стр. 39–44, 1953.
- также опубликовано как «Транзисторная метрология» , Труды профессиональной группы IRE по электронным устройствам , вып. ЭД-1, вып. 3, стр. 12–17, август 1954 г.
- Объединенный комитет AIEE-IRE, «Предлагаемые методы тестирования транзисторов» , Труды Американского института инженеров-электриков: связь и электроника , стр. 725–740, январь 1955 г.
- «Стандарты ИРЭ на полупроводниковые устройства: методы испытаний транзисторов, 1956» , Труды ИРЭ , вып. 44, вып. 11, стр. 1542–1561, ноябрь 1956 г.
- Стандартные методы тестирования транзисторов IEEE , стандарт IEEE 218-1956.
















































![{\displaystyle {\begin{aligned}\left[\mathbf {a} \right]&={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix }}= {\begin{bmatrix}A&B\\C&D\end{bmatrix}}\\\left[\mathbf {b} \right]&={\begin{bmatrix}b_{11}&b_{12}\\ b_{21}&b_{22}\end{bmatrix}}={\begin{bmatrix}A'&B'\\C'&D'\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe60a2e91eed9d330d67b88e847ac941a80a6e15)



















![{\displaystyle [\mathbf {z} ]=[\mathbf {z} ]_{1}+[\mathbf {z} ]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d93c3b805eacf076a46da4960464dfb35c5ae42)
![{\displaystyle [\mathbf {z} ]_{1}={\begin{bmatrix}R_{1}+R_{2}&R_{2}\\R_{2}&R_{2}\end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/624b40889c2e23222e58c9cff7e45dcf5254d7fc)
![{\displaystyle [\mathbf {z} ]=[\mathbf {z} ]_{1}+[\mathbf {z} ]_{2}=2[\mathbf {z} ]_{1}={\ начало{bmatrix}2R_{1}+2R_{2}&2R_{2}\\2R_{2}&2R_{2}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a87c81e4932a379081dd9f8a83c832b9fb59c51f)
![{\displaystyle [\mathbf {z} ]={\begin{bmatrix}R_{1}+2R_{2}&2R_{2}\\2R_{2}&2R_{2}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c94c69dc5621642b55480ac5c227ffbab8728774)
![{\displaystyle [\mathbf {y} ]=[\mathbf {y} ]_{1}+[\mathbf {y} ]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4b23ac0551ec8cee6df7d885d685c8a0f6f5ea)
![{\displaystyle [\mathbf {h} ]=[\mathbf {h} ]_{1}+[\mathbf {h} ]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e35a43ce4c044bd1ac2c19441531de4c216c21)
![{\displaystyle [\mathbf {g} ]=[\mathbf {g} ]_{1}+[\mathbf {g} ]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a33bf7723488619480c4ad8cfe1890c80ab50e6)
![{\displaystyle [\mathbf {a} ]=[\mathbf {a} ]_{1} \cdot [\mathbf {a} ]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d4153b087ac95879a7bc36b6bd348859dad989e)
![{\displaystyle [\mathbf {b} ]=[\mathbf {b} ]_{2} \cdot [\mathbf {b} ]_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23d8c4316d1feb0a2ad2bd2edf9efd3624b5753a)
![{\displaystyle {\begin{aligned}[][\mathbf {b} ]_{1}&={\begin{bmatrix}1&-R\\0&1\end{bmatrix}}\\\lbrack \mathbf {b } \rbrack _{2}&={\begin{bmatrix}1&0\\-sC&1\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/992ae0ff8794fb1c16d75fb3c48eb73b19fcd05b)
![{\displaystyle {\begin{aligned}[]\lbrack \mathbf {b} \rbrack &=\lbrack \mathbf {b} \rbrack _ {2} \cdot \lbrack \mathbf {b} \rbrack _{1} \\&={\begin{bmatrix}1&0\\-sC&1\end{bmatrix}}{\begin{bmatrix}1&-R\\0&1\end{bmatrix}}\\&={\begin{bmatrix}1& -R\\-sC&1+sCR\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ac012b86277c8b8826fec66f77b11270cfca371)


![{\displaystyle {\frac {1}{\Delta \mathbf {[y]} }}{\begin{bmatrix}y_{22}&-y_{12}\\-y_{21}&y_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c88ffe2d04c66ea158cce57f580cd5267abce0e)
![{\displaystyle {\frac {1}{h_{22}}}{\begin{bmatrix}\Delta \mathbf {[h]} &h_{12}\\-h_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/679350eeb4501fdcbb765109982cba5ee87702cb)
![{\displaystyle {\frac {1}{g_{11}}}{\begin{bmatrix}1&-g_{12}\\g_{21}&\Delta \mathbf {[g]} \end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7571ffabfe73601c1f386526f47f7cb93df0dc21)
![{\displaystyle {\frac {1}{a_{21}}}{\begin{bmatrix}a_{11} &\Delta \mathbf {[a]} \\1&a_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2854821de24f97e711f6663b0b4b90f5365fcb1)
![{\displaystyle {\frac {1}{b_{21}}}{\begin{bmatrix}-b_{22}&-1\\-\Delta \mathbf {[b]} &-b_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b42b94e8f71b186b145ef74378c440bb77ac2387)
![{\displaystyle {\frac {1}{\Delta \mathbf {[z]} }}{\begin{bmatrix}z_{22}&-z_{12}\\-z_{21}&z_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/487dab825b656f1e0a2d73e74172948e52da3a91)

![{\displaystyle {\frac {1}{h_{11}}}{\begin{bmatrix}1&-h_{12}\\h_{21}&\Delta \mathbf {[h]} \end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/04bd8b306b3b259f0137fa39e0d23636bf9dd095)
![{\displaystyle {\frac {1}{g_{22}}}{\begin{bmatrix}\Delta \mathbf {[g]} &g_{12}\\-g_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f1754d13c9fd54602ce8548754165b669811e3d)
![{\displaystyle {\frac {1}{a_{12}}}{\begin{bmatrix}a_{22}&-\Delta \mathbf {[a]} \\-1&a_{11}\end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c802d740f72fc6175de957e2cf1ee95f3cbc4c93)
![{\displaystyle {\frac {1}{b_{12}}}{\begin{bmatrix}-b_{11}&1\\\Delta \mathbf {[b]} &-b_{22}\end{bmatrix} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb283ff7b662b2be5dee2ed4b60a5cf06c8a949)
![{\displaystyle {\frac {1}{z_{22}}}{\begin{bmatrix}\Delta \mathbf {[z]} &z_{12}\\-z_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3547f1e5ce30efd98cfadc48955972100ef1fb7)
![{\displaystyle {\frac {1}{y_{11}}}{\begin{bmatrix}1&-y_{12}\\y_{21}&\Delta \mathbf {[y]} \end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e108f5071a85ed3923a1eee1f1b01280651019e8)

![{\displaystyle {\frac {1}{\Delta \mathbf {[g]} }}{\begin{bmatrix}g_{22}&-g_{12}\\-g_{21}&g_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8460f7065162ca83b30f80322090b39409a2f993)
![{\displaystyle {\frac {1}{a_{22}}}{\begin{bmatrix}a_{12} &\Delta \mathbf {[a]} \\-1&a_{21}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73f2d30b43344b899a3d580c9839d711bcfaa088)
![{\displaystyle {\frac {1}{b_{11}}}{\begin{bmatrix}-b_{12}&1\\-\Delta \mathbf {[b]} &-b_{21}\end{bmatrix }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b3d40e5e3b4804b2bf4ae9bb4d7a6a3466a9ec)
![{\displaystyle {\frac {1}{z_{11}}}{\begin{bmatrix}1&-z_{12}\\z_{21}&\Delta \mathbf {[z]} \end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/632efee553a0074f0a53f3728daabc61efc228e2)
![{\displaystyle {\frac {1}{y_{22}}}{\begin{bmatrix}\Delta \mathbf {[y]} &y_{12}\\-y_{21}&1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07b0048de9c42457c78987ff24cdbb163413041f)
![{\displaystyle {\frac {1}{\Delta \mathbf {[h]} }}{\begin{bmatrix}h_{22}&-h_{12}\\-h_{21}&h_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/732cd41db04bcb0d04be3afe420d93bf926501f5)

![{\displaystyle {\frac {1}{a_{11}}}{\begin{bmatrix}a_{21}&-\Delta \mathbf {[a]} \\1&a_{12}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc02229992524f2d4b9b2ff429081aa8c3259dd)
![{\displaystyle {\frac {1}{b_{22}}}{\begin{bmatrix}-b_{21}&-1\\\Delta \mathbf {[b]} &-b_{12}\end{ бматрица}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65e27a58d182069a1604adea4d34a0414c235965)
![{\displaystyle {\frac {1}{z_{21}}}{\begin{bmatrix}z_{11} &\Delta \mathbf {[z]} \\1&z_{22}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9e1df73c8bd4dff60b2bc2eadc0abb52eead96d)
![{\displaystyle {\frac {1}{y_{21}}}{\begin{bmatrix}-y_{22}&-1\\-\Delta \mathbf {[y]} &-y_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68c776cac7d0c011700f7ce937cffd37455c38d4)
![{\displaystyle {\frac {1}{h_{21}}}{\begin{bmatrix}-\Delta \mathbf {[h]} &-h_{11}\\-h_{22}&-1\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea019358559b8ba1b9ae3abb899e3db9e1875475)
![{\displaystyle {\frac {1}{g_{21}}}{\begin{bmatrix}1&g_{22}\\g_{11}&\Delta \mathbf {[g]} \end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269fc51350d7ded4803b758f27ff12cb80e73beb)

![{\displaystyle {\frac {1}{\Delta \mathbf {[b]} }}{\begin{bmatrix}b_{22}&-b_{12}\\-b_{21}&b_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86ca4b289ed3c07c833c3001ee10168d417a42ab)
![{\displaystyle {\frac {1}{z_{12}}}{\begin{bmatrix}z_{22}&-\Delta \mathbf {[z]} \\-1&z_{11}\end{bmatrix}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c40fe17c9e9399ea4ada9238208b9d8e7a99098)
![{\displaystyle {\frac {1}{y_{12}}}{\begin{bmatrix}-y_{11}&1\\\Delta \mathbf {[y]} &-y_{22}\end{bmatrix} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33262946d25e353d1f51cc00e9372c153b105fbd)
![{\displaystyle {\frac {1}{h_{12}}}{\begin{bmatrix}1&-h_{11}\\-h_{22}&\Delta \mathbf {[h]} \end{bmatrix} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69984c19e2082dea86e684591755600b7d2d43de)
![{\displaystyle {\frac {1}{g_{12}}}{\begin{bmatrix}-\Delta \mathbf {[g]} &g_{22}\\g_{11}&-1\end{bmatrix} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc585f3a56517316e99dafcf64df6d476b2618a)
![{\displaystyle {\frac {1}{\Delta \mathbf {[a]} }}{\begin{bmatrix}a_{22}&-a_{12}\\-a_{21}&a_{11}\end {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122338c08414e1803e057a4a3d235287d6492234)

![{\displaystyle {\begin{aligned}\left[\mathbf {y} \right]&=[\mathbf {z} ]^{-1}\\\left[\mathbf {g} \right]&=[ \mathbf {h} ]^{-1}\\\left[\mathbf {b} \right]&=[\mathbf {a} ]^{-1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc26bb8c637cf7e990cdf8b37682da1f4db4f8e4)



![{\displaystyle {\begin{aligned}I_{2}&=-{\frac {Z_{21}}{Z_{\mathrm {L} }+Z_{22}}}I_{1}\\[3pt] V_{1}&=Z_{11}I_{1}-{\frac {Z_{12}Z_{21}}{Z_{\mathrm {L} }+Z_{22}}}I_{1}\\ [2pt]&=\left(Z_{11}-{\frac {Z_{12}Z_{21}}{Z_{\mathrm {L} }+Z_{22}}}\right)I_{1}= Z_{\text{in}}I_{1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d54360b5992aacc324b4f8571e5027bdc6bc783)
