Соленоидальное векторное поле

Пример соленоидального векторного поля: $\mathbf {v} (x,y)=(y,-x)$

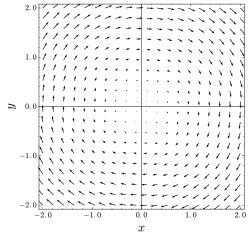
В векторном исчислении соленоидальное векторное поле (также известное как несжимаемое векторное поле , векторное поле без дивергенций или поперечное векторное поле ) представляет собой векторное поле v с нулевой дивергенцией во всех точках поля: $$\nabla \cdot \mathbf {v} =0.$$Обычный способ выразить это свойство — сказать, что поле не имеет источников и стоков.

Характеристики

Теорема о дивергенции дает эквивалентное интегральное определение соленоидального поля; а именно, что для любой замкнутой поверхности чистый общий поток через поверхность должен быть равен нулю:

$\;\;\mathbf {v} \cdot \,d\mathbf {S} =0,$

где $d\mathbf {S}$ — внешняя нормаль к каждому элементу поверхности.

Фундаментальная теорема векторного исчисления гласит, что любое векторное поле можно выразить как сумму безвихревого и соленоидального полей. Условие нулевой дивергенции выполняется всякий раз, когда векторное поле v имеет только компонент векторного потенциала , поскольку определение векторного потенциала A выглядит следующим образом: $$\mathbf {v} =\nabla \times \mathbf {A}$$автоматически приводит к тождеству (что можно показать, например, с помощью декартовых координат): $$\nabla \cdot \mathbf {v} =\nabla \cdot (\nabla \times \mathbf {A} )=0.$$ : Верно и обратное для любого соленоида v существует вектор-потенциал A такой, что $\mathbf {v} =\nabla \times \mathbf {A} .$ (Строго говоря, это справедливо при соблюдении определенных технических условий на v , см. разложение Гельмгольца .)

Этимология

Соленоид имеет свое происхождение от греческого слова, обозначающего соленоид , которое означает σωληνοειδές (sōlēnoeidēs), что означает трубообразный, от σωλην (sōlēn) или труба.

Примеры

• Магнитное поле B (см. закон Гаусса для магнетизма )
• Поле скоростей потока несжимаемой жидкости
• Поле завихренности ​
• Электрическое поле E в нейтральных областях ( $\rho _{e}=0$);
• Плотность тока J при неизменной плотности заряда ${\textstyle {\frac {\partial \rho _{e}}{\partial t}}=0}$.
• Магнитный векторный потенциал A в кулоновской калибровке

См. также

• Продольные и поперечные векторные поля
• Функция потока
• Консервативное векторное поле

Ссылки

• Арис, Резерфорд (1989), Векторы, тензоры и основные уравнения механики жидкости , Дувр, ISBN  0-486-66110-5