Угол контакта

Угол контакта (символ $θ C$ ) - угол между жидкости поверхностью и твердой поверхностью, где они встречаются. Более конкретно, это угол между поверхностной касательной жидкости и паров на границе раздела и касательными на границе с твердым сплошным, на их пересечении. Он количественно определяет смачиваемость твердой поверхности жидкостью через молодое уравнение .

Заданная система твердой, жидкости и пара при заданной температуре и давлении имеет уникальный угла контакта равновесия. Тем не менее, на практике часто наблюдается динамическое явление гистерезиса угла контакта , начиная с ускоряющегося (максимального) угла контакта до угла контакта с перерыванием (минимальным). ^{[ 1 ]} Контакт равновесия находится в пределах этих значений и может быть рассчитан на них. Угол контакта равновесия отражает относительную прочность жидкости, твердого и парамолевого взаимодействия .

Угол контакта зависит от среды над свободной поверхностью жидкости, а также от природы жидкости и твердого вещества в контакте. Он не зависит от наклона твердого вещества к поверхности жидкости. Он меняется с поверхностным натяжением и, следовательно, с температурой и чистотой жидкости.

Термодинамика

Теоретическое описание угла контакта возникает из -за рассмотрения термодинамического равновесия между тремя фазами : жидкая фаза (L), твердая фаза (ы) и фаза газа или пара (G) (которая может быть смесью окружающей среды Атмосфера и равновесная концентрация жидкого пара). («Газовая» фаза может быть заменена другой неизменной твердого вещества жидкой фазой.) Если межфазная энергия обозначается $γ SG$ , межфазной энергии твердости с помощью $γ SL$ энергии жидко и межфазной натяжение ) с помощью $γ LG$ , тогда угла равновесного контакта $θ C$ определяется из этих величин молодым уравнением : $\gamma _{\rm {SG}}-\gamma _{\rm {SL}}-\gamma _{\rm {LG}}\cos \theta _{\rm {C}}=0\,$

Угол контакта также может быть связан с работой адгезии через уравнение молодых и юпри : $\gamma _{\rm {LG}}(1+\cos \theta _{\rm {C}})=\Delta W_{\rm {SLG}}\,$

где $\Delta W_{\rm {SLG}}$ является твердым - энергией адгезии жидкости на единицу площади, когда в среде G.

Модифицированное уравнение Янга

Самое раннее исследование взаимосвязи между углом контакта и поверхностной напряженностью для сидячих капель на плоских поверхностях было сообщено Томасом Янгом в 1805 году. ^{[ 2 ]} Спустя столетие Гиббс ^{[ 3 ]} предложил модификацию уравнения Янга для учета объемной зависимости угла контакта. Гиббс постулировал существование линейного натяжения, которое действует на трехфазной границе и объясняет избыточную энергию при слиянии границы с твердоэтажным газом и дается как:

$\cos \theta ={\frac {\gamma _{\rm {SG}}-\gamma _{\rm {SL}}}{\gamma _{\rm {LG}}}}+{\frac {\kappa }{\gamma _{\rm {LG}}}}{\frac {1}{a}}$

где $κ$ - это линейное напряжение в Ньютонах , а $А$ - радиус капли в метрах. Хотя экспериментальные данные подтверждают аффинную связь между косинусом угла контакта и радиусом обратной линии, это не учитывает правильный признак $κ$ и переоценивает его значение на несколько порядков.

Прогноз угла контакта при учете линейного натяжения и давления в Лапласе

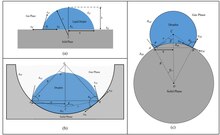
С улучшениями в методах измерения, таких как атомная силовая микроскопия , конфокальная микроскопия и сканирующий электронный микроскоп , исследователи смогли продуцировать и капли изображения в все меньших масштабах. С уменьшением размера капель появилось новые экспериментальные наблюдения за смачиванием. Эти наблюдения подтвердили, что модифицированное уравнение Янга не удерживается в микроанановых масштабах. Джаспер ^{[ 5 ]}^{[ 4 ]} Предполагается, что включение $термина V DP$ в изменение свободной энергии может быть ключом к решению задачи угла контакта в таких небольших масштабах. Учитывая, что изменение свободной энергии равна нулю в равновесии:

$0={\frac {dA_{\rm {LG}}}{dA_{\rm {SL}}}}+{\frac {\gamma _{\rm {SL}}-\gamma _{\rm {SG}}}{\gamma _{\rm {LG}}}}-{\frac {\kappa }{\gamma _{\rm {LG}}}}{\frac {dL}{dA_{\rm {SL}}}}-{\frac {V}{\gamma _{\rm {LG}}}}{\frac {dP}{dA_{\rm {SL}}}}$

Изменение давления на границе свободного жидкости в жидкости обусловлено давлением Лапласа, которое пропорционально средней кривизны. Решение вышеупомянутого уравнения как для выпуклых, так и для вогнутых поверхностей дает: ^{[ 4 ]}

$\cos(\theta \mp \alpha )=A+B\,{\frac {\cos \alpha }{a}}\pm C\sin(\theta \mp \alpha )(1+\cos \theta )^{2}{\biggl (}{\frac {\sin \alpha \,(2+\cos \alpha )}{(1+\cos \alpha )^{2}}}\mp {\frac {\sin \theta \,(2+\cos \theta )}{(1+\cos \theta )^{2}}}{\biggr )}$

где $A={\frac {\gamma _{\rm {SG}}-\gamma _{\rm {SL}}}{\gamma _{\rm {LG}}}},\quad B={\frac {\kappa }{\gamma _{\rm {LG}}}},\quad C={\frac {\gamma }{3\gamma _{\rm {LG}}}}.$

Это уравнение связывает угол контакта, геометрическое свойство сидячей капли с объемной термодинамикой, энергией на трехфазной границе контакта и средней кривизны капли. Для особого случая сидячей капли на плоской поверхности ( $α = 0$ ):

$\cos \theta ={\frac {\gamma _{\rm {SG}}-\gamma _{\rm {SL}}}{\gamma _{\rm {LG}}}}+{\frac {\kappa }{\gamma _{\rm {LG}}}}{\frac {1}{a}}-{\frac {\gamma }{3\gamma _{\rm {LG}}}}(2+\cos \theta -2\cos ^{2}\theta -\cos ^{3}\theta )$

В приведенном выше уравнении первые два термина являются модифицированным уравнением Янга, а третий член связан с давлением Лапласа. Это нелинейное уравнение правильно предсказывает знак и величину $κ$ , уплотнение угла контакта в очень маленьких масштабах и гистерезис угла контакта.

Гистерезис угла контакта

В данной комбинации субстрата-жидко-паров дает непрерывный диапазон значений угла контакта на практике. Максимальный угол контакта называется угла угла контакта, а минимальный угол контакта называется как угол контакта. Угрящиеся и отступающие углы контакта измеряются по динамическим экспериментам, где капли или жидкие мосты находятся в движении. ^{[ 1 ]} Напротив, угол контакта равновесия, описанный уравнением молодого лаверса, измеряется из статического состояния. Статические измерения дают значения между продвигающим и отступающим угол контакта в зависимости от параметров осаждения (например, скорость, угол и размер падения) и историю падения (например, испарение со времен отложения). Гистерезис угла контакта определяется как $θ A - θ R,$ хотя термин также используется для описания выражения $cos θ r - cos θ a$ . Статический, продвигающий или отступающий угол контакта может использоваться вместо равновесного угла контакта в зависимости от применения. Общий эффект можно рассматривать как близко аналогичный статическим трениям , то есть для перемещения контактной линии требуется минимальное количество работы на единицу расстояния. ^{[ 6 ]}

Угольный угол контакта может быть описан как мера сплоченности жидкости и солидности, в то время как угол контакта перерыва является мерой адгезии жидкости. Угрящиеся углы контакта могут быть измерены непосредственно с использованием различных методов, а также могут быть рассчитаны по другим измерениям смачивания, таким как силовая тенсиометрия (он же метод Wilhemy Plate ).

Угрящие и отступающие углы контакта могут быть измерены непосредственно из того же измерения, если капли перемещаются линейно на поверхности. Например, капля жидкости примет заданный угол контакта в статике, но когда поверхность наклоняется, капля первоначально деформируется так, что площадь контакта между каплей и поверхностью оставалась постоянной. Сторона «вниз» от падения примет более высокий угол контакта, в то время как «подъемная» сторона капля примет более низкий угол контакта. По мере увеличения угла наклона углы контакта будут продолжать меняться, но площадь контакта между каплей и поверхностью останется постоянной. При заданном углу наклона поверхности будут выполнены углы контакта, и капля будет двигаться на поверхности. На практике на измерение может зависеть от сдвиговых сил и импульса, если скорость наклона высока. Метод измерения также может быть сложным на практике для систем с высоким (> 30 градусов) или низким (<10 градусов) гистерезис угла контакта.

Добавление и измерение угла контакта может быть выполнено путем добавления и удаления жидкости из капли на поверхности. Если в падение добавлен достаточно небольшой объем жидкости, линия контакта все еще будет закреплена, а угол контакта увеличится. Точно так же, если небольшое количество жидкости удаляется из капли, угол контакта уменьшится.

Уравнение Янга принимает однородную поверхность и не учитывает текстуру поверхности или внешние силы, такие как гравитация. Реальные поверхности не являются атомно гладкими или химически гомогенными, поэтому капля предполагает гистерезис угла контакта. Угол контакта равновесия ( $θ C$ ) можно рассчитать из $θ A$ и $θ R,$ как было показано теоретически TADMOR ^{[ 7 ]} и подтвердил экспериментально Чибовски ^{[ 8 ]} как,

$\theta _{\rm {c}}=\arccos \left({\frac {r_{\rm {A}}\cos \theta _{\rm {A}}+r_{\rm {R}}\cos \theta _{\rm {R}}}{r_{\rm {A}}+r_{\rm {R}}}}\right)$

где

${\begin{aligned}r_{\rm {A}}&={\sqrt[{3}]{\frac {\sin ^{3}\theta _{\rm {A}}}{2-3\cos \theta _{\rm {A}}+\cos ^{3}\theta _{\rm {A}}}}}\\[4pt]r_{\rm {R}}&={\sqrt[{3}]{\frac {\sin ^{3}\theta _{\rm {R}}}{2-3\cos \theta _{\rm {R}}+\cos ^{3}\theta _{\rm {R}}}}}\end{aligned}}$

На поверхности, которая является шероховатой или загрязненной, также будет гистерезис угла контакта, но теперь локальный угол контакта равновесия (молодое уравнение теперь только локально достоверное) может варьироваться от места к месту на поверхности. ^{[ 9 ]} Согласно уравнению молодого -дюпра, это означает, что энергия адгезии варьируется локально - таким образом, жидкость должна преодолеть локальные энергетические барьеры, чтобы намочить поверхность. Одним из последствий этих барьеров является гистерезис угла контакта : степень смачивания и, следовательно, наблюдаемый угол контакта (усредненный вдоль контактной линии) зависит от того, продвигается ли жидкость или отступает на поверхности.

Поскольку жидкость достигает ранее сухой поверхности, но отступает от ранее влажной поверхности, гистерезис угла контакта также может возникнуть, если твердование было изменено из -за его предыдущего контакта с жидкостью (например, химической реакцией или поглощением). Такие изменения, если они медленны, также могут создавать измеримо зависимых от времени углов контакта.

Влияние шероховатости для контактных углов

Шероховатость поверхности оказывает сильное влияние на угол контакта и смачиваемость поверхности. Эффект шероховатости зависит от того, будет ли капля намочить поверхностные канавки или остаются ли воздушные карманы между каплей и поверхностью. ^{[ 10 ]}

Если поверхность смачивается гомогенно, капля находится в состоянии Венцеля. ^{[ 11 ]} В штате Венцель добавление шероховатости поверхности увеличит смачиваемость, вызванную химией поверхности. Корреляция Венцеля может быть написана как $\cos \theta _{m}=r\cos \theta _{Y}$ где $θ M$ - измеренный угол контакта, $θ y$ - это угол контакта молодого, а $R$ - это отношение шероховатости. Коэффициент шероховатости определяется как отношение между фактической и проецируемой площадью твердой поверхности.

Если поверхность смачивается гетерогенно, капля находится в состоянии Кэсси-Бакстер. ^{[ 12 ]} Самый стабильный угол контакта может быть подключен к молодому углу контакта. Было обнаружено, что углы контакта, рассчитанные по уравнениям Венцеля и Кэсси-Бакстера, являются хорошими приближениями наиболее стабильных углов контакта с реальными поверхностями. ^{[ 13 ]}

Динамические углы контакта

Для быстрого движения жидкости через поверхность угол контакта может быть изменен с его значения в состоянии покоя. Угнутый угол контакта будет увеличиваться со скоростью, а угол контакта отступления уменьшится. Расхождения между статическими и динамическими углами контакта тесно пропорциональны капиллярному номеру , отмеченный $Ca$ . ^{[ 1 ]}

Кривиза контакта

На основании межфазных энергий, профиль поверхностного капли или жидкого моста между двумя поверхностями может быть описан уравнением молодого лапласа . ^{[ 1 ]} Это уравнение применимо для трехмерных осесимметричных условий и очень нелинейно. Это связано со средним термином кривизны , который включает в себя продукты производных первого и второго порядка функции формы капель $f(x,y)$ : $\kappa _{m}={\frac {1}{2}}{\frac {(1+{f_{x}}^{2})f_{yy}-2f_{x}f_{y}f_{xy}+(1+{f_{y}}^{2})f_{xx}}{(1+{f_{x}}^{2}+{f_{y}}^{2})^{3/2}}}.$

Решение этого эллиптического дифференциального уравнения , которое регулирует форму трехмерного падения в сочетании с соответствующими граничными условиями, является сложной, и обычно принимается подход минимизации альтернативной энергии. Формы трехмерных сидячих и подвесных капель были успешно предсказаны с использованием этого метода минимизации энергии. ^{[ 14 ]}

Типичные углы контакта

Капля воды на поверхности листа лотоса, показывающая углы контакта примерно 147 °.

Контактные углы чрезвычайно чувствительны к загрязнению; Значения, воспроизводимые в лучшее, чем несколько градусов, обычно получаются только в лабораторных условиях с очищенными жидкостями и очень чистыми твердыми поверхностями. Если молекулы жидкости сильно притягиваются к твердым молекулам, то капля жидкости полностью распространится на твердой поверхности, что соответствует углу контакта 0 °. Это часто относится к воде на обнаженных металлических или керамических поверхностях, ^{[ 15 ]} Хотя присутствие оксидного слоя или загрязняющих веществ на твердой поверхности может значительно увеличить угол контакта. Как правило, если угол контакта воды меньше 90 °, твердость поверхность считается гидрофильной ^{[ 16 ]} И если угол контакта воды больше 90 °, твердотельная поверхность считается гидрофобной . Многие полимеры демонстрируют гидрофобные поверхности. Высокодорофобные поверхности, изготовленные из низкоповерхностной энергии (например, фторированных ) материалов, могут иметь углы контакта с водой до ≈ 120 °. ^{[ 15 ]} Некоторые материалы с очень грубыми поверхностями могут иметь угол контакта с водой даже более 150 °, из -за присутствия воздушных карманов под каплей жидкости. Они называются супергидрофобными поверхностями.

Если угол контакта измеряется через газ, а не через жидкость, то его следует заменить на 180 ° за вычетом их данного значения. Контактные углы одинаково применимы к границе раздела двух жидкостей, хотя они чаще измеряются в твердых изделиях, таких как кастрюли без стиков и водонепроницаемые ткани .

Контроль углов контакта

Контроль угла контакта смачивания часто может быть достигнут за счет осаждения или включения различных органических и неорганических молекул на поверхность. Это часто достигается за счет использования специализированных силановых химических веществ, которые могут образовывать слой SAM (самооборные монослои). При правильном выборе органических молекул с различными молекулярными структурами и количествами углеводородов и/или перфторированных завершений, угол контакта поверхности может настраивать. Показания этих специализированных силанов ^{[ 17 ]} может быть достигнуто в газовой фазе с помощью специализированных вакуумных печи или жидкофейного процесса. Молекулы, которые могут связывать более перфторированные выборы с поверхностью, могут привести к снижению поверхностной энергии (высокий угол контакта воды).

Влияние поверхностного фтора на угол контакта	Угол контакта воды
Предшественник	на полированном кремнии (град.)
Хенкозил-1,1,2,2-тетрагидродододододотододецилдиметилтрис (диметиламинозилан)	118.0
Heptadecafluoro-1,1,2,2-тетрагидродецилтрихлорзилан- (FDTS)	110.0
Nonafluoro-1,1,2,2-тетрагидрогексилтрис (диметиламино)	110.0
3,3,3,4,4,5,5,6,6-ненафлуорогексилтрихлорсилан	108.0
Tridecafluoro-1,1,2,2-тетрагидзоктилтрихлорзилан-(Фоты)	108.0
Bis (Tridecafluoro-1,1,2,2-тетрагидзоктил) диметилсилоксиметилхлорзилан	107.0
Додецилтрихлорсилан - (ДДТ)	105.0
Диметилдихлорсилан - (DDMS)	103.0
10-Undecenyltrichlorosilane-(v11)	100.0
Пентафторофенилпропилтрихлорсилан	90.0

Измерение методов

Метод статического сидячего падения

Угол контакта с сидячим выпуском измеряется гониометром угла контакта с использованием оптической подсистемы для захвата профиля чистой жидкости на твердой подложке. Угол, сформированный между границей жидкости -слида и границей жидкости -парона, является углом контакта. Старые системы использовали оптическую систему микроскопа с задним светом. Системы текущего поколения используют камеры высокого разрешения и программное обеспечение для захвата и анализа угла контакта. Углы, измеренные таким образом, часто довольно близки к продвижению углов контакта. Равновесные углы контакта могут быть получены путем применения четко определенных вибраций. ^{[ 18 ]}^{[ 19 ]}

Метод броска подвеска

Измерение углов контакта для подвесных капель гораздо сложнее, чем для сидячих капель из -за нестабильной природы перевернутых капель. Эта сложность дополнительно усиливается, когда кто -то пытается склонить поверхность. Экспериментальный аппарат для измерения углов контакта подвесной контакты на наклонных субстратах был разработан недавно. ^{[ 20 ]} Этот метод допускает осаждение множества микроропов на нижней стороне текстурированного субстрата, которую можно отображать с помощью CCD -камеры высокого разрешения. Автоматизированная система позволяет наклонять подложку и анализировать изображения для расчета продвигающихся и отступающих углов контакта.

Динамический метод отступления

Динамическое сидячие падения аналогична статической сидячей падке, но требует изменения капли. Распространенный тип исследования динамического сидячих капель определяет наибольший угол контакта без увеличения его твердого жидкости межфазной области путем динамического добавления объема. Этот максимальный угол - угол продвижения. Объем удаляется, чтобы получить наименьший возможный угол, угол отступления. Разница между углом продвигающегося и отмены заключается в гистерезисе угла контакта . ^{[ 19 ]}

Динамический метод Вильгельми

Динамический метод Вильгельми - это метод для расчета средних прогрессирующих и отступающих углов контакта на твердых частиц однородной геометрии. Обе стороны твердого вещества должны иметь одинаковые свойства. Сила смачивания на твердого вещества измеряется, когда твердое вещество погружается в или снимается из жидкости известного поверхностного натяжения. Также в этом случае можно измерить равновесный угол контакта, применяя очень контролируемую вибрацию. Эта методология, называемая VIECA, может быть реализована довольно простым способом на каждом балансе Вильгельми . ^{[ 21 ]}

Одноволокно Wilhelmy Method

Динамический метод Вильгельми, применяемый к отдельным волокнам для измерения продвигающихся и отступающих контактных углов.

Метод мениска с одним волокном

Оптическое изменение одного волоконного метода Вильгельми. Вместо измерения с балансом форма мениска на волокне напрямую отображается с помощью камеры высокого разрешения. Автоматизированная подгонка формы мениска может затем напрямую измерить статический, продвигающий или отступающий угол контакта на волокне.

Метод повышения капилляров уравнений Washburn

В случае пористых материалов многие вопросы были подняты как о физическом значении расчетного диаметра пор, так и о реальной возможности использования этого уравнения для расчета угла контакта твердого вещества, даже если этот метод часто предлагается большим программным обеспечением. как консолидировано. ^{[ 22 ]}^{[ нужно разъяснения ]} Измеряется изменение веса в зависимости от времени. ^{[ 23 ]}

Смотрите также

Ссылки

^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Ши, Z.; и др. (2018). «Динамический гистерезис угла контакта в жидких мостах». Коллоиды и поверхности A: физико -химические и инженерные аспекты . 555 : 365–371. Arxiv : 1712.04703 . doi : 10.1016/j.colsurfa.2018.07.004 . S2CID 51916594 .
^ «III. Эссе о сплоченности жидкостей» . Философские транзакции Королевского общества Лондона . 95 : 65–87. Январь 1805 года. DOI : 10.1098/rstl.1805.0005 . ISSN 0261-0523 . S2CID 116124581 .
^ Гиббс, Дж. Уиллард (Джозия Уиллард) (1961). Научные статьи . Dover Publications. ISBN 978-0486607214 Полем OCLC 964884 .
^ Jump up to: ^а ^{беременный} ^в Джаспер, Уоррен Дж.; Ананд, Надиш (май 2019). «Обобщенный вариационный подход для прогнозирования углов контакта сидячих нано-капель на плоских и изогнутых поверхностях». Журнал молекулярных жидкостей . 281 : 196–203. doi : 10.1016/j.molliq.2019.02.039 . ISSN 0167-7322 . S2CID 104412970 .
^ Джаспер, Уоррен Дж.; Расипурам, Сринивасан (декабрь 2017 г.). «Связь между угла контакта и радиусом контактной линии для микро -до Atto [от 10 до 10-18] литров. Журнал молекулярных жидкостей . 248 : 920–926. doi : 10.1016/j.molliq.2017.10.134 . ISSN 0167-7322 .
^ Хаттори, Цуйоши; Кошизука, Сейичи (2019). «Численное моделирование поведения капель на наклонной пластине с использованием полумамозового метода движущихся частиц» . Журнал машиностроения . 6 (5): 19-00204–19-00204. doi : 10.1299/mej.19-00204 . ISSN 2187-9745 .
^ Tadmor, Rafael (2004). «Энергия линии и связь между продвижением, отстранением и молодыми углами контакта». Langmuir . 20 (18): 7659–64. doi : 10.1021/la049410h . PMID 15323516 .
^ Chibowski, Emil (2008). «Свободная энергия поверхности серы - заселенная I. Желтые и оранжевые образцы, затвердевшие на стеклянной поверхности». Журнал коллоидной и интерфейсной науки . 319 (2): 505–13. Bibcode : 2008jcis..319..505c . doi : 10.1016/j.jcis.2007.10.059 . PMID 18177886 .
^ De Gennes, PG (1985). «Смачивание: статика и динамика». Обзоры современной физики . 57 (3): 827–863. Bibcode : 1985rvmp ... 57..827d . doi : 10.1103/revmodphys.57.827 .
^ «Влияние шероховатости поверхности на угол контакта и смачиваемость» (PDF) .
^ Венцель, Роберт Н. (1936-08-01). «Сопротивление твердых поверхностей к смачиванию водой». Промышленная и инженерная химия . 28 (8): 988–994. doi : 10.1021/IE50320A024 . ISSN 0019-7866 .
^ Кэсси, Абд; Бакстер С. (1944-01-01). «Смачиваемость пористых поверхностей». Труды общества Фарадея . 40 : 546. DOI : 10.1039/TF9444000546 . ISSN 0014-7672 .
^ Мармур, Авраам (2009-07-06). «Сплошная характеристика путем смачивания». Ежегодный обзор исследований материалов . 39 (1): 473–489. Bibcode : 2009anrms..39..473m . doi : 10.1146/annurev.matsci.38.060407.132425 . ISSN 1531-7331 .
^ Chen Y, He B, Lee J, Patankar NA (2005). «Анизотропия при смачивании грубых поверхностей» (PDF) . Журнал коллоидной и интерфейсной науки . 281 (2): 458–464. Bibcode : 2005jcis..281..458c . doi : 10.1016/j.jcis.2004.07.038 . PMID 15571703 . Архивировано из оригинала (PDF) 2017-08-10 . Получено 2017-03-31 .
^ Jump up to: ^а ^{беременный} Зисман, Вашингтон (1964). Ф. Фоукс (ред.). Угол контакта, смачиваемость и адгезия . Кондиционер С. 1–51.
^ Ренате Фёрч; Хольгер Шёнхерр; А. Тобиас А. Дженкинс (2009). Дизайн поверхности: применение в биологической науке и нанотехнологиях . Wiley-Vch. п. 471. ISBN 978-3-527-40789-7 .
^ Kobrin, B.; Zhang, T.; Чинн . Дж 209 -е собрание электрохимического общества, 7–12 мая 2006 г., Денвер, co .
^ Volpe, CD; Бругнара, М.; Maniglio, D.; Siboni, S.; Wangdu, T. (2006). «О возможности экспериментального измерения равновесного угла контакта и его теоретических и практических последствий» . Угол контакта, смачиваемость и адгезия . 4 : 79–100.
^ Jump up to: ^а ^{беременный} Huhtamäki, Tommi; Тянь, Xuelin; Korhonen, Juuso T.; Рас, Робин Х.А. (2018). «Характеристика поверхности с использованием измерений контактного угла» . Природные протоколы . 13 (7): 1521–1538. doi : 10.1038/s41596-018-0003-z . ISSN 1754-2189 . PMID 29988109 . S2CID 51605807 .
^ Бутани, Гаурав; Muralidhar, K.; Кхандкар, Самир (2013). «Определение кажущегося угла контакта и формы статического подвесного падения на физически текстурированной наклонной поверхности». Межфазные явления и теплопередача . 1 : 29–49. doi : 10.1615/InterfacphenomHeatTransfer.2013007038 .
^ Volpe, CD; Maniglio, D.; Siboni, S.; Морра М. (2001). «Экспериментальная процедура получения равновесного угла контакта из метода Вильгельми» (PDF) . Нефтегазовая наука и технология . 56 : 9–22. doi : 10.2516/ogst: 2001002 .
^ Марко, Бругнара; Клаудио, Делла Вольпе; Стефано, Сибони (2006). «Смачиваемость пористых материалов. II. Можем ли мы получить угол контакта из уравнения Washburn?». В Миттале, Кл (ред.). Угол контакта, смачиваемость и адгезия . Mass. VSP.
^ Washburn, Edward W. (1921). «Динамика капиллярного потока» . Физический обзор . 17 (3): 273. Bibcode : 1921phrv ... 17..273w . doi : 10.1103/physrev.17.273 .

Дальнейшее чтение

Пьер-Жиль де Геннес , Франсуаз Брохард-Виарт, Дэвид Квере, явления капиллярности и смачивания: капли, пузырьки, жемчужины, волны , Springer (2004)
Джейкоб Исраелахвили , Межмолекулярные и поверхностные силы , Академическая пресса (1985–2004)
DW Van Krevelen, Properties of Polymers , 2-е пересмотренное издание, Elsevier Scientific Publishing Company, Амстердам-Оксфорд-Нью-Йорк (1976)
Юань, Юэхуа; Ли, Т. Рэндалл (2013). «Угол контакта и смачивающие свойства». Поверхностные науки . Серия Springer в Surface Sciences. Тол. 51. doi : 10.1007/978-3-642-34243-1 . ISBN 978-3-642-34242-4 Полем ISSN 0931-5195 . S2CID 137147527 .
Clegg, Carl Contact Engle сделан Easy , Ramé-Hart (2013), ISBN 978-1-300-66298-3

[CAH-1] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Ши, Z.; и др. (2018). «Динамический гистерезис угла контакта в жидких мостах». Коллоиды и поверхности A: физико -химические и инженерные аспекты . 555 : 365–371. Arxiv : 1712.04703 . doi : 10.1016/j.colsurfa.2018.07.004 . S2CID 51916594 .

[2] «III. Эссе о сплоченности жидкостей» . Философские транзакции Королевского общества Лондона . 95 : 65–87. Январь 1805 года. DOI : 10.1098/rstl.1805.0005 . ISSN 0261-0523 . S2CID 116124581 .

[3] Гиббс, Дж. Уиллард (Джозия Уиллард) (1961). Научные статьи . Dover Publications. ISBN 978-0486607214 Полем OCLC 964884 .

[Jasper_196–203-4] Jump up to: ^а ^{беременный} ^в Джаспер, Уоррен Дж.; Ананд, Надиш (май 2019). «Обобщенный вариационный подход для прогнозирования углов контакта сидячих нано-капель на плоских и изогнутых поверхностях». Журнал молекулярных жидкостей . 281 : 196–203. doi : 10.1016/j.molliq.2019.02.039 . ISSN 0167-7322 . S2CID 104412970 .

[5] Джаспер, Уоррен Дж.; Расипурам, Сринивасан (декабрь 2017 г.). «Связь между угла контакта и радиусом контактной линии для микро -до Atto [от 10 до 10-18] литров. Журнал молекулярных жидкостей . 248 : 920–926. doi : 10.1016/j.molliq.2017.10.134 . ISSN 0167-7322 .

[HATTORIKOSHIZUKA2019-6] Хаттори, Цуйоши; Кошизука, Сейичи (2019). «Численное моделирование поведения капель на наклонной пластине с использованием полумамозового метода движущихся частиц» . Журнал машиностроения . 6 (5): 19-00204–19-00204. doi : 10.1299/mej.19-00204 . ISSN 2187-9745 .

[Tadm-7] Tadmor, Rafael (2004). «Энергия линии и связь между продвижением, отстранением и молодыми углами контакта». Langmuir . 20 (18): 7659–64. doi : 10.1021/la049410h . PMID 15323516 .

[Chib-8] Chibowski, Emil (2008). «Свободная энергия поверхности серы - заселенная I. Желтые и оранжевые образцы, затвердевшие на стеклянной поверхности». Журнал коллоидной и интерфейсной науки . 319 (2): 505–13. Bibcode : 2008jcis..319..505c . doi : 10.1016/j.jcis.2007.10.059 . PMID 18177886 .

[deGennes-9] De Gennes, PG (1985). «Смачивание: статика и динамика». Обзоры современной физики . 57 (3): 827–863. Bibcode : 1985rvmp ... 57..827d . doi : 10.1103/revmodphys.57.827 .

[10] «Влияние шероховатости поверхности на угол контакта и смачиваемость» (PDF) .

[11] Венцель, Роберт Н. (1936-08-01). «Сопротивление твердых поверхностей к смачиванию водой». Промышленная и инженерная химия . 28 (8): 988–994. doi : 10.1021/IE50320A024 . ISSN 0019-7866 .

[12] Кэсси, Абд; Бакстер С. (1944-01-01). «Смачиваемость пористых поверхностей». Труды общества Фарадея . 40 : 546. DOI : 10.1039/TF9444000546 . ISSN 0014-7672 .

[13] Мармур, Авраам (2009-07-06). «Сплошная характеристика путем смачивания». Ежегодный обзор исследований материалов . 39 (1): 473–489. Bibcode : 2009anrms..39..473m . doi : 10.1146/annurev.matsci.38.060407.132425 . ISSN 1531-7331 .

[14] Chen Y, He B, Lee J, Patankar NA (2005). «Анизотропия при смачивании грубых поверхностей» (PDF) . Журнал коллоидной и интерфейсной науки . 281 (2): 458–464. Bibcode : 2005jcis..281..458c . doi : 10.1016/j.jcis.2004.07.038 . PMID 15571703 . Архивировано из оригинала (PDF) 2017-08-10 . Получено 2017-03-31 .

[zisman-15] Jump up to: ^а ^{беременный} Зисман, Вашингтон (1964). Ф. Фоукс (ред.). Угол контакта, смачиваемость и адгезия . Кондиционер С. 1–51.

[16] Ренате Фёрч; Хольгер Шёнхерр; А. Тобиас А. Дженкинс (2009). Дизайн поверхности: применение в биологической науке и нанотехнологиях . Wiley-Vch. п. 471. ISBN 978-3-527-40789-7 .

[17] Kobrin, B.; Zhang, T.; Чинн . Дж 209 -е собрание электрохимического общества, 7–12 мая 2006 г., Денвер, co .

[18] Volpe, CD; Бругнара, М.; Maniglio, D.; Siboni, S.; Wangdu, T. (2006). «О возможности экспериментального измерения равновесного угла контакта и его теоретических и практических последствий» . Угол контакта, смачиваемость и адгезия . 4 : 79–100.

[:0-19] Jump up to: ^а ^{беременный} Huhtamäki, Tommi; Тянь, Xuelin; Korhonen, Juuso T.; Рас, Робин Х.А. (2018). «Характеристика поверхности с использованием измерений контактного угла» . Природные протоколы . 13 (7): 1521–1538. doi : 10.1038/s41596-018-0003-z . ISSN 1754-2189 . PMID 29988109 . S2CID 51605807 .

[bhutani-20] Бутани, Гаурав; Muralidhar, K.; Кхандкар, Самир (2013). «Определение кажущегося угла контакта и формы статического подвесного падения на физически текстурированной наклонной поверхности». Межфазные явления и теплопередача . 1 : 29–49. doi : 10.1615/InterfacphenomHeatTransfer.2013007038 .

[21] Volpe, CD; Maniglio, D.; Siboni, S.; Морра М. (2001). «Экспериментальная процедура получения равновесного угла контакта из метода Вильгельми» (PDF) . Нефтегазовая наука и технология . 56 : 9–22. doi : 10.2516/ogst: 2001002 .

[Brugnara-22] Марко, Бругнара; Клаудио, Делла Вольпе; Стефано, Сибони (2006). «Смачиваемость пористых материалов. II. Можем ли мы получить угол контакта из уравнения Washburn?». В Миттале, Кл (ред.). Угол контакта, смачиваемость и адгезия . Mass. VSP.

[washburn-23] Washburn, Edward W. (1921). «Динамика капиллярного потока» . Физический обзор . 17 (3): 273. Bibcode : 1921phrv ... 17..273w . doi : 10.1103/physrev.17.273 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]