Сегментированная регрессия
| Часть серии о |
| Регрессионный анализ |
|---|
| Модели |
| Оценка |
| Фон |
Сегментированная регрессия , также известная как кусочная регрессия или регрессия с ломаной линией , представляет собой метод регрессионного анализа , в котором независимая переменная разбивается на интервалы и каждому интервалу соответствует отдельный сегмент линии. Сегментированный регрессионный анализ также можно выполнить на многомерных данных путем разделения различных независимых переменных. Сегментированная регрессия полезна, когда независимые переменные, сгруппированные в разные группы, демонстрируют разные отношения между переменными в этих регионах. Границы между сегментами являются точками останова .
Сегментированная линейная регрессия — это сегментированная регрессия, при которой отношения в интервалах получаются с помощью линейной регрессии .
Сегментированная линейная регрессия, два сегмента
[ редактировать ]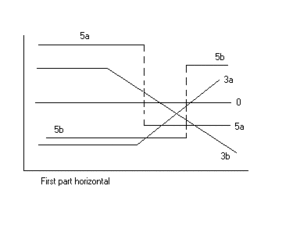


Сегментированная линейная регрессия с двумя сегментами, разделенными точкой останова, может быть полезна для количественной оценки резкого изменения функции отклика (Yr) варьирующегося влиятельного фактора ( x ). Точку останова можно интерпретировать как критическое , безопасное или пороговое значение, за которым или ниже которого возникают (не)желательные эффекты. Точка останова может быть важна при принятии решений. [1]
На рисунках показаны некоторые полученные результаты и типы регрессии.
Сегментированный регрессионный анализ основан на наличии набора данных ( y, x ), в которых y является зависимой переменной , а x — независимой переменной .
Метод наименьших квадратов применяется отдельно к каждому сегменту, с помощью которого две линии регрессии создаются так, чтобы максимально точно соответствовать набору данных, при этом минимизируя сумму квадратов разностей (SSD) между наблюдаемыми ( y ) и расчетными (Yr) значениями. зависимой переменной приводит к следующим двум уравнениям:
- Год = А 1 . x + K 1 для x < BP (точка останова)
- Год = А 2 . x + K 2 для x > BP (точка останова)
где:
- Yr — ожидаемое (прогнозированное) значение y для определенного значения x ;
- A 1 и A 2 — коэффициенты регрессии (обозначающие наклон отрезков линии);
- K 1 и K 2 являются константами регрессии (указывающими точку пересечения на оси y ).
Данные могут отражать множество типов или тенденций, [2] см. цифры.
Этот метод также дает два коэффициента корреляции (R):
- для x < BP (точка останова)
и
- для x > BP (точка останова)
где:
- это минимизированный SSD на сегмент
и
- Y a1 и Y a2 — средние значения y на соответствующих участках.
При определении наиболее подходящего тренда статистические тесты необходимо провести , чтобы убедиться, что этот тренд надежен (значим).
Когда не удается обнаружить значимую точку останова, необходимо вернуться к регрессии без точки останова.
Пример
[ редактировать ]
Для синего рисунка справа, который показывает связь между урожайностью горчицы (Yr = Ym, т/га) и засолением почвы ( x = Ss, выраженной как электропроводность почвенного раствора EC в дСм/м), обнаружено, что : [3]
БП = 4,93, А 1 = 0, К 1 = 1,74, А 2 = -0,129, К 2 = 2,38, Р 1 2 = 0,0035 (незначительно), R 2 2 = 0,395 (значимый) и:
- Ym = 1,74 т/га для Ss < 4,93 (точка перелома)
- Ym = −0,129 Ss + 2,38 т/га для Ss > 4,93 (точка перелома)
что указывает на то, что засоление почвы < 4,93 дСм/м является безопасным, а засоление почвы > 4,93 дСм/м снижает урожайность при 0,129 т/га на единицу увеличения засоления почвы.
На рисунке также показаны доверительные интервалы и неопределенность, как описано ниже.
Процедуры испытаний
[ редактировать ]
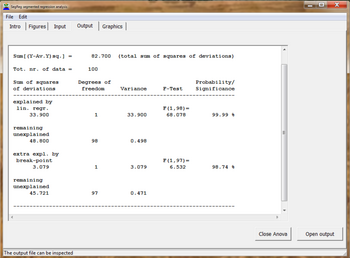
следующие статистические тесты Для определения типа тренда используются :
- значимость точки останова (BP) путем выражения BP как функции коэффициентов регрессии A 1 и A 2 и средних значений Y 1 и Y 2 данных y и средних значений X 1 и X 2 данных x (слева и справа). BP), используя законы распространения ошибок при сложении и умножении для вычисления стандартной ошибки (SE) BP и применяя t-критерий Стьюдента
- значимость A 1 и A 2 с применением t-распределения Стьюдента и стандартной ошибки SE A 1 и A 2
- значимость разницы A 1 и A 2 с применением t-распределения Стьюдента с использованием SE их разницы.
- значимость разницы Y 1 и Y 2 с применением t-распределения Стьюдента с использованием SE их разницы.
- Более формальный статистический подход к проверке существования точки останова заключается в тесте псевдооценки, который не требует оценки сегментированной линии. [4]
Кроме того, используются коэффициент корреляции всех данных (Ra), коэффициент детерминации или коэффициент объяснения, доверительные интервалы функций регрессии и анализ ANOVA . [5]
Коэффициент детерминации для всех данных (Cd), который должен быть максимизирован в условиях, установленных критериями значимости, находится из:
где Yr — ожидаемое (прогнозированное) значение y согласно предыдущим уравнениям регрессии, а Ya — среднее всех значений y .
Коэффициент Cd варьируется от 0 (полное отсутствие объяснения) до 1 (полное объяснение, идеальное совпадение).
В чистой несегментированной линейной регрессии значения Cd и Ra 2 равны. В сегментированной регрессии Cd должно быть значительно больше, чем Ra. 2 чтобы оправдать сегментацию.
Оптимальное был значение точки излома может быть найдено таким, чтобы коэффициент Cd максимальным .
Диапазон без эффекта
[ редактировать ]
Сегментированная регрессия часто используется для определения того, в каком диапазоне объясняющая переменная (X) не оказывает влияния на зависимую переменную (Y), в то время как за пределами досягаемости существует четкий ответ, будь то положительный или отрицательный.Область отсутствия эффекта может быть обнаружена в начальной части X-домена или, наоборот, в его последней части. Для анализа «без эффекта» применение метода наименьших квадратов для сегментного регрессионного анализа. [6] может быть не самым подходящим методом, поскольку цель состоит скорее в том, чтобы найти самый длинный участок, на котором можно считать, что отношение YX имеет нулевой наклон, в то время как за пределами досягаемости наклон значительно отличается от нуля, но знание о наилучшем значении этого наклона не материален. Методом определения диапазона отсутствия эффекта является прогрессивная частичная регрессия. [7] по диапазону, расширяя диапазон небольшими шагами до тех пор, пока коэффициент регрессии не станет значительно отличаться от нуля.
На следующем рисунке точка излома находится при X=7,9, в то время как для тех же данных (см. синий рисунок выше, где показан выход горчицы), метод наименьших квадратов дает точку излома только при X=4,9. Последнее значение ниже, но соответствие данных за точкой останова лучше. Следовательно, от цели анализа будет зависеть, какой метод необходимо использовать.
См. также
[ редактировать ]- Чау-тест
- Простая регрессия
- Линейная регрессия
- Обычные наименьшие квадраты
- Сплайны многомерной адаптивной регрессии
- Локальная регрессия
- Дизайн разрыва регрессии
- Пошаговая регрессия
- SegReg (программное обеспечение) для сегментированной регрессии
Ссылки
[ редактировать ]- ^ Частотный и регрессионный анализ . Глава 6 в: HPRitzema (изд., 1994), Принципы и применение дренажа , Publ. 16, стр. 175–224, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. ISBN 90-70754-33-9 . Бесплатная загрузка с веб-страницы [1] под номером. 20 или напрямую в формате PDF: [2]
- ^ Исследования дренажа на фермерских полях: анализ данных . Часть проекта «Жидкое золото» Международного института мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Скачать в формате PDF: [3]
- ^ RJOosterbaan, DPSharma, KNSingh и KVGKRao, 1990, Растениеводство и засоленность почвы: оценка полевых данных из Индии с помощью сегментированной линейной регрессии . В: Материалы симпозиума по дренажу земель для борьбы с засолением в засушливых и полузасушливых регионах, 25 февраля - 2 марта 1990 г., Каир, Египет, Vol. 3, Сессия V, с. 373 – 383.
- ^ Муггео, ВМР (2016). «Тестирование с мешающим параметром присутствует только в альтернативном варианте: подход на основе оценок с применением к сегментированному моделированию» (PDF) . Журнал статистических вычислений и моделирования . 86 (15): 3059–3067. дои : 10.1080/00949655.2016.1149855 . S2CID 124914264 .
- ^ Статистическая значимость сегментированной линейной регрессии с точкой излома с использованием дисперсионного анализа и F-тестов . Скачать из [4] под номером. 13 или напрямую в формате PDF: [5]
- ^ Сегментированный регрессионный анализ, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Бесплатная загрузка с веб-страницы [6]
- ^ Частичный регрессионный анализ, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Бесплатная загрузка с веб-страницы [7]



