Ядро (статистика)
Эта статья нуждается в дополнительных цитатах для проверки . ( май 2012 г. ) |
Термин «ядро» используется в статистическом анализе для обозначения оконной функции . Термин «ядро» имеет несколько различных значений в разных отраслях статистики.
Байесовская статистика
[ редактировать ]В статистике, особенно в байесовской статистике , ядро функции плотности вероятности (pdf) или функции массы вероятности (pmf) представляет собой форму PDF или pmf, в которой любые факторы, которые не являются функциями какой-либо из переменных в области, являются опущен. [1] Обратите внимание, что такие факторы вполне могут быть функциями параметров PDF или PMF. Эти факторы составляют часть коэффициента нормализации распределения вероятностей и во многих ситуациях не нужны. Например, при выборке псевдослучайных чисел большинство алгоритмов выборки игнорируют коэффициент нормализации. Кроме того, в байесовском анализе сопряженных априорных распределений коэффициенты нормализации обычно игнорируются во время вычислений и учитывается только ядро. В конце проверяется форма ядра, и если она соответствует известному распределению, коэффициент нормализации можно восстановить. В противном случае это может оказаться ненужным (например, если необходимо только выполнить выборку из дистрибутива).
Для многих распределений в замкнутой форме можно записать ядро, но не константу нормализации.
Примером является нормальное распределение . Его функция плотности вероятности равна
и связанное с ним ядро
Обратите внимание, что множитель перед экспонентой опущен, хотя он содержит параметр , потому что это не функция переменной домена .
Анализ шаблонов
[ редактировать ]Ядро воспроизводящего ядра гильбертова пространства используется в наборе методов, известных как методы ядра, для выполнения таких задач, как статистическая классификация , регрессионный анализ и кластерный анализ данных в неявном пространстве. Такое использование особенно распространено в машинном обучении .
Непараметрическая статистика
[ редактировать ]В непараметрической статистике ядро — это весовая функция, используемая в непараметрической методах оценки. Ядра используются при оценке плотности ядра для оценки величин случайных функций плотности или в регрессии ядра для оценки условного ожидания случайной величины. Ядра также используются во временных рядах при использовании периодограммы для оценки спектральной плотности , где они известны как оконные функции . Дополнительное использование заключается в оценке изменяющейся во времени интенсивности точечного процесса , где оконные функции (ядра) свертываются с данными временных рядов.
Обычно ширину ядра также необходимо указывать при выполнении непараметрической оценки.
Определение
[ редактировать ]Ядро — это неотрицательная с действительным знаком интегрируемая функция . Для большинства приложений желательно определить функцию, удовлетворяющую двум дополнительным требованиям:
- Симметрия:
Первое требование гарантирует, что метод оценки плотности ядра приводит к функции плотности вероятности . Второе требование гарантирует, что среднее соответствующего распределения будет равно среднему значению используемой выборки.
Если K является ядром, то так же является и функция K *, определяемая формулой K *( u ) = λ K (λ u ), где λ > 0. Это можно использовать для выбора масштаба, подходящего для данных.
Часто используемые функции ядра
[ редактировать ]
Обычно используются несколько типов ядерных функций: равномерная, треугольник, Епанечникова, [2] квартик (двухвесный), трикуб, [3] трехвесный, гауссовский, квадратичный [4] и косинус.
В таблице ниже, если задано с ограниченным носителем , то для значений u, лежащих вне опоры.
| Функции ядра, K ( u ) | Эффективность [5] относительно ядра Епанечникова | ||||
|---|---|---|---|---|---|
| Униформа («прямоугольное окно») | Поддерживать: |  | 92.9% | ||
| Треугольный | Поддерживать: | 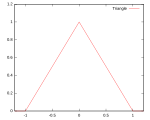 | 98.6% | ||
| Епанечников (параболический) | Поддерживать: |  | 100% | ||
| Квартик (полувесовой вес) | Поддерживать: | 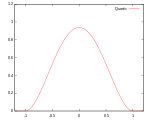 | 99.4% | ||
| Трехвесный вес | Поддерживать: |  | 98.7% | ||
| Трехкуб | Поддерживать: |  | 99.8% | ||
| Гауссовский | 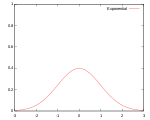 | 95.1% | |||
| Косинус | Поддерживать: | 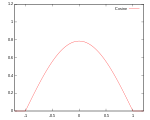 | 99.9% | ||
| Логистика |  | 88.7% | |||
| Сигмовидная функция |  | 84.3% | |||
| Ядро Сильвермана [6] |  | непригодный | |||
См. также
[ редактировать ]- Оценка плотности ядра
- Ядро более гладкое
- Стохастическое ядро
- Положительно определенное ядро
- Оценка плотности
- Многомерная оценка плотности ядра
- Метод ядра
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( Май 2012 г. ) |
Ссылки
[ редактировать ]- ^ Шустер, Юджин (август 1969 г.). «Оценка функции плотности вероятности и ее производных» . Анналы математической статистики . 40 (4): 1187–1195. дои : 10.1214/aoms/1177697495 .
- ^ Назван в честь Епанечников, В.А. (1969). «Непараметрическая оценка многомерной плотности вероятности». Теория вероятностей. Приложение . 14 (1): 153–158. дои : 10.1137/1114019 .
- ^ Альтман, Н.С. (1992). «Введение в непараметрическую регрессию ядра и ближайшего соседа». Американский статистик . 46 (3): 175–185. дои : 10.1080/00031305.1992.10475879 . hdl : 1813/31637 .
- ^ Кливленд, Вашингтон ; Девлин, С.Дж. (1988). «Локально взвешенная регрессия: подход к регрессионному анализу путем локальной подгонки». Журнал Американской статистической ассоциации . 83 (403): 596–610. дои : 10.1080/01621459.1988.10478639 .
- ^ Эффективность определяется как .
- ^ Сильверман, BW (1986). Оценка плотности для статистики и анализа данных . Чепмен и Холл, Лондон.
- Ли, Ци; Расин, Джеффри С. (2007). Непараметрическая эконометрика: теория и практика . Издательство Принстонского университета. ISBN 978-0-691-12161-1 .
- Цуккини, Уолтер. «ПРИКЛАДНЫЕ МЕТОДЫ СГЛАЖИВАНИЯ. Часть 1: Оценка плотности ядра» (PDF) . Проверено 6 сентября 2018 г.
- Команичиу, Д; Меер, П. (2002). «Сдвиг среднего: надежный подход к анализу пространства признаков». Транзакции IEEE по анализу шаблонов и машинному интеллекту . 24 (5): 603–619. CiteSeerX 10.1.1.76.8968 . дои : 10.1109/34.1000236 .











































