Многомерная оценка плотности ядра

Оценка плотности ядра — это непараметрический метод оценки плотности , т. е. оценки функций плотности вероятности , что является одним из фундаментальных вопросов статистики . Его можно рассматривать как обобщение оценки плотности гистограмм с улучшенными статистическими свойствами. Помимо гистограмм, другие типы оценок плотности включают параметрические , сплайновые , вейвлет-ряды и ряды Фурье . Оценщики плотности ядра были впервые представлены в научной литературе для одномерных данных в 1950-х и 1960-х годах. ^[1]^[2] и впоследствии получили широкое распространение. Вскоре было признано, что аналогичные оценки для многомерных данных станут важным дополнением к многомерной статистике . Согласно исследованиям, проведенным в 1990-х и 2000-х годах, многомерная ядерная оценка плотности достигла уровня зрелости, сравнимого с ее одномерными аналогами. ^[3]^[4]^[5]

Мотивация

Мы возьмем иллюстративный синтетический набор двумерных данных из 50 точек, чтобы проиллюстрировать построение гистограмм. Для этого необходимо выбрать опорную точку (левый нижний угол сетки гистограммы). Для гистограммы слева мы выбираем (-1,5, -1,5): для гистограммы справа мы сдвигаем опорную точку на 0,125 в обоих направлениях до (-1,625, -1,625). Обе гистограммы имеют ширину интервала 0,5, поэтому любые различия обусловлены только изменением опорной точки. Цветовое кодирование указывает количество точек данных, попадающих в интервал: 0 = белый, 1 = бледно-желтый, 2 = ярко-желтый, 3 = оранжевый, 4 = красный. Левая гистограмма, по-видимому, указывает на то, что верхняя половина имеет более высокую плотность, чем нижняя половина, тогда как для правой гистограммы наблюдается обратное, что подтверждает, что гистограммы очень чувствительны к расположению опорной точки. ^[6]

Одним из возможных решений этой проблемы размещения опорных точек является полное удаление сетки группировки гистограммы. На левом рисунке ниже ядро (представленное серыми линиями) центрировано в каждой из 50 точек данных выше. Результат суммирования этих ядер показан на рисунке справа и представляет собой оценку плотности ядра. Самое поразительное различие между оценками плотности ядра и гистограммами заключается в том, что первые легче интерпретировать, поскольку они не содержат искусственных элементов, вызванных сеткой биннинга. Цветные контуры соответствуют наименьшей области, содержащей соответствующую массу вероятности: красный = 25%, оранжевый + красный = 50%, желтый + оранжевый + красный = 75%, что указывает на то, что одна центральная область имеет наибольшую плотность.

Цель оценки плотности — взять конечную выборку данных и сделать выводы об основной функции плотности вероятности везде, в том числе там, где данные не наблюдаются. При оценке плотности ядра вклад каждой точки данных сглаживается из одной точки в окружающую ее область пространства. Агрегирование индивидуально сглаженных вкладов дает общую картину структуры данных и их функции плотности. Далее мы покажем, что этот подход приводит к разумной оценке основной функции плотности.

Определение

Предыдущий рисунок представляет собой графическое представление оценки плотности ядра, которую мы теперь определяем точным образом. Пусть x ₁ , x ₂ , ..., x _n будут выборкой с d -вариантами, случайных векторов взятыми из общего распределения, описываемого функцией плотности ƒ . Оценка плотности ядра определяется как

{\hat {f}}_{\mathbf {H} }(\mathbf {x} )={\frac {1}{n}}\sum _{i=1}^{n}K_{\mathbf {H} }(\mathbf {x} -\mathbf {x} _{i})

где

Икс знак равно ( Икс ₁ , Икс ₂ , …, Икс _d ) ^Т, Икс _я знак равно ( Икс _{я 1} , Икс _{я 2} , …, Икс _{идентификатор} ) ^Т, i = 1, 2, …, n — d -векторы;
H полосы пропускания (или сглаживания), — матрица d×d которая является симметричной и положительно определенной ;
K — ядерная функция, представляющая собой симметричную многомерную плотность;
$K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ .

Выбор функции ядра K не имеет решающего значения для точности оценок плотности ядра, поэтому мы повсюду используем стандартное многомерное нормальное ядро: ${\textstyle K_{\mathbf {H} }(\mathbf {x} )={(2\pi )^{-d/2}}\mathbf {|H|} ^{-1/2}e^{-{\frac {1}{2}}\mathbf {x^{T}} \mathbf {H^{-1}} \mathbf {x} }}$ , где H играет роль ковариационной матрицы . С другой стороны, выбор матрицы полосы пропускания H является единственным наиболее важным фактором, влияющим на ее точность, поскольку он контролирует величину и ориентацию вызванного сглаживания. ^[3]^: 36–39 То, что матрица полосы пропускания также вызывает ориентацию, является основным отличием многомерной оценки плотности ядра от ее одномерного аналога, поскольку ориентация не определена для одномерных ядер. Это приводит к выбору параметризации этой матрицы полосы пропускания. Три основных класса параметризации (в порядке возрастания сложности): S , класс положительных скаляров, умноженных на единичную матрицу; D , диагональные матрицы с положительными элементами на главной диагонали; и F — симметричные положительно определенные матрицы. Ядра класса S имеют одинаковую степень сглаживания, применяемую во всех координатных направлениях, ядра D допускают различную степень сглаживания по каждой из координат, а ядра F допускают произвольную величину и ориентацию сглаживания. Исторически ядра S и D являются наиболее распространенными из-за вычислительных причин, но исследования показывают, что значительный выигрыш в точности можно получить, используя более общие ядра F- класса. ^[7]^[8]

Выбор оптимальной матрицы полосы пропускания

Наиболее часто используемым критерием оптимальности для выбора матрицы полосы пропускания является MISE или среднеинтегральная квадратичная ошибка.

\operatorname {MISE} (\mathbf {H} )=\operatorname {E} \!\left[\,\int ({\hat {f}}_{\mathbf {H} }(\mathbf {x} )-f(\mathbf {x} ))^{2}\,d\mathbf {x} \;\right].

Обычно это не имеет выражения в замкнутой форме , поэтому обычно используют его асимптотическое приближение (AMISE) в качестве прокси.

\operatorname {AMISE} (\mathbf {H} )=n^{-1}|\mathbf {H} |^{-1/2}R(K)+{\tfrac {1}{4}}m_{2}(K)^{2}(\operatorname {vec} ^{T}\mathbf {H} )\mathbf {\Psi } _{4}(\operatorname {vec} \mathbf {H} )

где

$R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ) знак р ( K равно (4 π ) ^{−d /2} когда K — нормальное ядро
$\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ ,

где I _d — d × d единичная матрица , где m ₂ = 1 для нормального ядра

Д ²ƒ - матрица Гессе размера d × d частных производных второго порядка от ƒ
$\mathbf {\Psi } _{4}=\int (\operatorname {vec} \,\operatorname {D} ^{2}f(\mathbf {x} ))(\operatorname {vec} ^{T}\operatorname {D} ^{2}f(\mathbf {x} ))\,d\mathbf {x}$ это д ² × д ² матрица интегрированных частных производных четвертого порядка от ƒ
vec — векторный оператор, который объединяет столбцы матрицы в один вектор, например $\operatorname {vec} {\begin{bmatrix}a&c\\b&d\end{bmatrix}}={\begin{bmatrix}a&b&c&d\end{bmatrix}}^{T}.$

Качество приближения AMISE к MISE ^[3]^: 97 дается

\operatorname {MISE} (\mathbf {H} )=\operatorname {AMISE} (\mathbf {H} )+o(n^{-1}|\mathbf {H} |^{-1/2}+\operatorname {tr} \,\mathbf {H} ^{2})

где o означает обычное маленькое обозначение o . Эвристически это утверждение подразумевает, что AMISE является «хорошей» аппроксимацией MISE при размере выборки n → ∞.

Можно показать, что любой разумный селектор полосы пропускания H имеет H = O ( n ^{−2/( д +4)}), где большое обозначение O применяется поэлементно. Подставив это в формулу MISE, получим, что оптимальный MISE равен O ( n ^{−4/( д +4)}). ^[3]^: 99–100 Таким образом, при n → ∞ MISE → 0, т. е. оценка плотности ядра сходится в среднеквадратическом , а значит, и в вероятности, к истинной плотности f . Эти способы сходимости являются подтверждением утверждения в разделе «Мотивация» о том, что ядерные методы приводят к разумным оценкам плотности. Идеальным селектором оптимальной полосы пропускания является

\mathbf {H} _{\operatorname {AMISE} }=\operatorname {argmin} _{\mathbf {H} \in F}\,\operatorname {AMISE} (\mathbf {H} ).

Поскольку этот идеальный селектор содержит неизвестную функцию плотности ƒ , его нельзя использовать напрямую. Множество различных разновидностей селекторов полосы пропускания на основе данных возникают из-за разных оценок AMISE. Мы сосредоточимся на двух классах селекторов, которые, как было доказано, наиболее широко применимы на практике: сглаженная перекрестная проверка и подключаемые селекторы.

Плагин

Плагин (PI) оценка AMISE формируется путем замены Ψ ₄ его оценщиком ${\hat {\mathbf {\Psi } }}_{4}$

\operatorname {PI} (\mathbf {H} )=n^{-1}|\mathbf {H} |^{-1/2}R(K)+{\tfrac {1}{4}}m_{2}(K)^{2}(\operatorname {vec} ^{T}\mathbf {H} ){\hat {\mathbf {\Psi } }}_{4}(\mathbf {G} )(\operatorname {vec} \,\mathbf {H} )

где ${\hat {\mathbf {\Psi } }}_{4}(\mathbf {G} )=n^{-2}\sum _{i=1}^{n}\sum _{j=1}^{n}[(\operatorname {vec} \,\operatorname {D} ^{2})(\operatorname {vec} ^{T}\operatorname {D} ^{2})]K_{\mathbf {G} }(\mathbf {X} _{i}-\mathbf {X} _{j})$ . Таким образом ${\hat {\mathbf {H} }}_{\operatorname {PI} }=\operatorname {argmin} _{\mathbf {H} \in F}\,\operatorname {PI} (\mathbf {H} )$ — это переключатель плагинов. ^[9]^[10] Эти ссылки также содержат алгоритмы оптимальной оценки матрицы G полосы пропускания пилот-сигнала и устанавливают, что ${\hat {\mathbf {H} }}_{\operatorname {PI} }$ по вероятности к HAMISE _{сходится} .

Сглаженная перекрестная проверка

Сглаженная перекрестная проверка (SCV) — это подмножество более крупного класса методов перекрестной проверки . Оценка SCV отличается от подключаемой оценки во втором члене.

\operatorname {SCV} (\mathbf {H} )=n^{-1}|\mathbf {H} |^{-1/2}R(K)+n^{-2}\sum _{i=1}^{n}\sum _{j=1}^{n}(K_{2\mathbf {H} +2\mathbf {G} }-2K_{\mathbf {H} +2\mathbf {G} }+K_{2\mathbf {G} })(\mathbf {X} _{i}-\mathbf {X} _{j})

Таким образом ${\hat {\mathbf {H} }}_{\operatorname {SCV} }=\operatorname {argmin} _{\mathbf {H} \in F}\,\operatorname {SCV} (\mathbf {H} )$ это селектор SCV. ^[10]^[11] Эти ссылки также содержат алгоритмы оптимальной оценки матрицы G полосы пропускания пилот-сигнала и устанавливают, что ${\hat {\mathbf {H} }}_{\operatorname {SCV} }$ сходится по вероятности HAMISE _к .

Эмпирическое правило

Эмпирическое правило Сильвермана предлагает использовать ${\sqrt {\mathbf {H} _{ii}}}=\left({\frac {4}{d+2}}\right)^{\frac {1}{d+4}}n^{\frac {-1}{d+4}}\sigma _{i}$ , где $\sigma _{i}$ - стандартное отклонение i-й переменной и $d$ количество измерений, а $\mathbf {H} _{ij}=0,i\neq j$ . Правило Скотта ${\sqrt {\mathbf {H} _{ii}}}=n^{\frac {-1}{d+4}}\sigma _{i}$ .

Асимптотический анализ

В разделе выбора оптимальной полосы пропускания мы представили MISE. Его построение основано на ожидаемом значении и дисперсии оценки плотности. ^[3]^: 97

\operatorname {E} {\hat {f}}(\mathbf {x} ;\mathbf {H} )=K_{\mathbf {H} }*f(\mathbf {x} )=f(\mathbf {x} )+{\frac {1}{2}}m_{2}(K)\operatorname {tr} (\mathbf {H} \operatorname {D} ^{2}f(\mathbf {x} ))+o(\operatorname {tr} \,\mathbf {H} )

где * — оператор свертки между двумя функциями, а

\operatorname {Var} {\hat {f}}(\mathbf {x} ;\mathbf {H} )=n^{-1}|\mathbf {H} |^{-1/2}R(K)f(\mathbf {x} )+o(n^{-1}|\mathbf {H} |^{-1/2}).

Чтобы эти два выражения были четко определены, мы требуем, чтобы все элементы H стремились к 0 и чтобы n ⁻¹ | Ч | ^−1/2 стремится к 0, поскольку n стремится к бесконечности. Принимая эти два условия, мы видим, что ожидаемое значение стремится к истинной плотности f, т. е. ядерная оценка плотности является асимптотически несмещенной ; и что дисперсия стремится к нулю. Использование стандартного разложения среднеквадратических значений

\operatorname {MSE} \,{\hat {f}}(\mathbf {x} ;\mathbf {H} )=\operatorname {Var} {\hat {f}}(\mathbf {x} ;\mathbf {H} )+[\operatorname {E} {\hat {f}}(\mathbf {x} ;\mathbf {H} )-f(\mathbf {x} )]^{2}

мы имеем, что MSE стремится к 0, подразумевая, что ядро оценки плотности является (среднеквадратическим) последовательным и, следовательно, сходится по вероятности к истинной плотности f . Скорость сходимости MSE к 0 обязательно равна скорости MISE, отмеченной ранее O ( n ^−4/(д+4)), следовательно, скорость сходимости оценки плотности к f равна O _p (n ^{−2/( д +4)}), где O _p обозначает порядок по вероятности . Это устанавливает поточечную сходимость. Функциональная сходимость устанавливается аналогичным образом, рассматривая поведение MISE и отмечая, что при достаточной регулярности интегрирование не влияет на скорость сходимости.

Для рассматриваемых селекторов полосы пропускания на основе данных целью является матрица полосы пропускания AMISE. Мы говорим, что селектор на основе данных сходится к селектору AMISE с относительной скоростью O _p ( n ^{− а}), а > 0, если

\operatorname {vec} ({\hat {\mathbf {H} }}-\mathbf {H} _{\operatorname {AMISE} })=O(n^{-2\alpha })\operatorname {vec} \mathbf {H} _{\operatorname {AMISE} }.

Было установлено, что подключаемый модуль и сглаженный селектор перекрестной проверки (с учетом одной полосы пропускания пилот-сигнала G ) сходятся с относительной скоростью O _p ( n ^{−2/( д +6)}) ^[10]^[12] т. е. оба этих селектора на основе данных являются непротиворечивыми оценщиками.

Оценка плотности с помощью матрицы полной полосы пропускания

Пакет кс ^[13] в R реализованы подключаемые модули и селекторы сглаженной перекрестной проверки (среди прочего). Этот набор данных (включенный в базовый дистрибутив R) содержит 272 записи по два измерения каждая: продолжительность извержения (минуты) и время время ожидания до следующего извержения (минуты) гейзера Old Faithful в Йеллоустонском национальном парке, США.

Фрагмент кода вычисляет оценку плотности ядра с помощью подключаемой матрицы пропускной способности. ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ Опять же, цветные контуры соответствуют наименьшей области, содержащей соответствующую массу вероятности: красный = 25%, оранжевый + красный = 50%, желтый + оранжевый + красный = 75%. Чтобы вычислить селектор SCV, Hpi заменяется на Hscv. Здесь она не отображается, поскольку во многом аналогична оценке плагина для этого примера.

library(ks)
data(faithful)
H <- Hpi(x=faithful)
fhat <- kde(x=faithful, H=H)
plot(fhat, display="filled.contour", drawpoints=TRUE, cex=0.5, pch=16, col.pt=1)

Оценка плотности с помощью диагональной матрицы полосы пропускания

Рассмотрим оценку плотности гауссовой смеси $(4 π ) −1 ехр(- .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1 ⁄ 2 ( х 1 2 + х2 2 )) + (4 п ) −1 ехр(- 1 ⁄ 2 (( х 1 – 3,5) 2 + х2 2 ))$ , от 500 случайно сгенерированных баллов. Мы используем программу Matlab для 2-мерные данные . Процедура представляет собой метод автоматического выбора полосы пропускания, специально разработанный для ядра Гаусса второго порядка. ^[14] На рисунке показана оценка плотности соединений, полученная в результате использования автоматически выбранной полосы пропускания.

Matlab-скрипт для примера

Введите следующие команды в Matlab после загрузка и сохраняем функцию kde2d.m в текущем каталоге.

  clear all  
  % generate synthetic data
  data=[randn(500,2);
      randn(500,1)+3.5, randn(500,1);];
  % call the routine, which has been saved in the current directory 
  [bandwidth,density,X,Y]=kde2d(data);
  % plot the data and the density estimate
  contour3(X,Y,density,50), hold on
  plot(data(:,1),data(:,2),'r.','MarkerSize',5)

Альтернативные критерии оптимальности

MISE – это ожидаемое интегрированное расстояние L ₂ между оценкой плотности и истинной функцией плотности f . Он наиболее широко используется, в основном из-за его простоты, и в большинстве программ реализованы селекторы полосы пропускания на основе MISE. Существуют альтернативные критерии оптимальности, которые пытаются охватить случаи, когда MISE не является подходящей мерой. ^[4]^{: 34–37, 78} Эквивалентная мера L ₁ , средняя интегрированная абсолютная ошибка, равна

\operatorname {MIAE} (\mathbf {H} )=\operatorname {E} \,\int |{\hat {f}}_{\mathbf {H} }(\mathbf {x} )-f(\mathbf {x} )|\,d\mathbf {x} .

Его математический анализ значительно сложнее, чем MISE. На практике выигрыш оказывается незначительным. ^[15] Норма L _∞ — это средняя равномерная абсолютная ошибка.

\operatorname {MUAE} (\mathbf {H} )=\operatorname {E} \,\operatorname {sup} _{\mathbf {x} }|{\hat {f}}_{\mathbf {H} }(\mathbf {x} )-f(\mathbf {x} )|.

который был исследован лишь кратко. ^[16] Критерии ошибки правдоподобия включают критерии, основанные на среднем расхождении Кульбака – Лейблера.

\operatorname {MKL} (\mathbf {H} )=\int f(\mathbf {x} )\,\operatorname {log} [f(\mathbf {x} )]\,d\mathbf {x} -\operatorname {E} \int f(\mathbf {x} )\,\operatorname {log} [{\hat {f}}(\mathbf {x} ;\mathbf {H} )]\,d\mathbf {x}

и среднее расстояние Хеллингера

\operatorname {MH} (\mathbf {H} )=\operatorname {E} \int ({\hat {f}}_{\mathbf {H} }(\mathbf {x} )^{1/2}-f(\mathbf {x} )^{1/2})^{2}\,d\mathbf {x} .

KL можно оценить с помощью метода перекрестной проверки, хотя селекторы перекрестной проверки KL могут быть неоптимальными, даже если они остаются согласованными для функций ограниченной плотности. ^[17] Селекторы MH были кратко рассмотрены в литературе. ^[18]

Все эти критерии оптимальности являются мерами, основанными на расстоянии, и не всегда соответствуют более интуитивным представлениям о близости, поэтому в ответ на эту проблему были разработаны более визуальные критерии. ^[19]

Объективный и основанный на данных выбор ядра

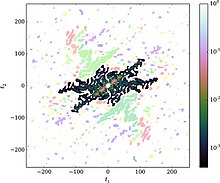
Недавние исследования показали, что ядро и его пропускная способность могут быть оптимально и объективно выбраны из самих входных данных, не делая никаких предположений о форме распределения. ^[20] Полученная оценка плотности ядра быстро сходится к истинному распределению вероятностей по мере добавления выборок: со скоростью, близкой к $n^{-1}$ ожидается для параметрических оценщиков. ^[20]^[21]^[22] Этот оценщик ядра работает как для одномерных, так и для многомерных выборок. Оптимальное ядро определяется в пространстве Фурье как оптимальная функция демпфирования ${\hat {\psi _{h}}}({\vec {t}})$ (преобразование Фурье ядра ${\hat {K}}({\vec {x}})$ )-- с точки зрения преобразования Фурье данных ${\hat {\varphi }}({\vec {t}})$ , эмпирическая характеристическая функция (см. Оценка плотности ядра ):

${\hat {\psi _{h}}}({\vec {t}})\equiv {\frac {N}{2(N-1)}}\left[1+{\sqrt {1-{\frac {4(N-1)}{N^{2}|{\hat {\varphi }}({\vec {t}})|^{2}}}}}I_{\vec {A}}({\vec {t}})\right]$ ^[22]

${\hat {f}}(x)={\frac {1}{(2\pi )^{d}}}\int {\hat {\varphi }}({\vec {t}})\psi _{h}({\vec {t}})e^{-i{\vec {t}}\cdot {\vec {x}}}d{\vec {t}}$

где N — количество точек данных, d — количество измерений (переменных), а $I_{\vec {A}}({\vec {t}})$ — фильтр, который равен 1 для «принимаемых частот» и 0 в противном случае. Существуют различные способы определения этой функции фильтра, и самый простой из них, который работает для одномерных или многомерных выборок, называется «фильтром наименьшего непрерывного гиперобъема»; $I_{\vec {A}}({\vec {t}})$ выбирается таким образом, чтобы единственные принимаемые частоты представляли собой непрерывное подмножество частот, окружающих начало координат, для которого $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ (видеть ^[22] для обсуждения этой и других функций фильтра).

Обратите внимание, что прямой расчет эмпирической характеристической функции (ECF) выполняется медленно, поскольку по существу включает прямое преобразование Фурье выборок данных. Однако было обнаружено, что ECF можно точно аппроксимировать с помощью метода неоднородного быстрого преобразования Фурье (nuFFT). ^[21]^[22] что увеличивает скорость вычислений на несколько порядков (в зависимости от размерности задачи). называется fastKDE . Комбинация этого объективного метода KDE и приближения ECF на основе nuFFT в литературе ^[22]

Демонстрация fastKDE на примере PDF-файла. (а) настоящий PDF, (б) хорошее представление с помощью fastKDE и (в) слегка размытое представление. — Нетривиальная смесь нормальных распределений: (а) базовый PDF, (б) оценка fastKDE на 1 000 000 выборок и (в) оценка fastKDE на 10 000 выборок.

См. также

Оценка плотности ядра – одномерная оценка плотности ядра.
Оценка плотности переменного ядра - оценка многомерных плотностей с использованием ядра с переменной полосой пропускания.

Ссылки

^ Розенблатт, М. (1956). «Замечания о некоторых непараметрических оценках функции плотности» . Анналы математической статистики . 27 (3): 832–837. дои : 10.1214/aoms/1177728190 .
^ Парзен, Э. (1962). «Об оценке функции плотности вероятности и режима» . Анналы математической статистики . 33 (3): 1065–1076. дои : 10.1214/aoms/1177704472 .
^ Jump up to: ^а ^б ^с ^д ^и Ванд, член парламента; Джонс, MC (1995). Сглаживание ядра . Лондон: Чепмен и Холл/CRC. ISBN 9780412552700 .
^ Jump up to: ^а ^б Симонов, Дж. С. (1996). Методы сглаживания в статистике . Спрингер. ISBN 9780387947167 .
^ Чакон, Дж. Э. и Дуонг, Т. (2018). Многомерное ядровое сглаживание и его применение . Чепмен и Холл/CRC. ISBN 9781498763011 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Сильверман, BW (1986). Оценка плотности для статистики и анализа данных . Чепмен и Холл/CRC. стр. 7–11 . ISBN 9780412246203 .
^ Ванд, член парламента; Джонс, MC (1993). «Сравнение параметризаций сглаживания при двумерной оценке плотности ядра». Журнал Американской статистической ассоциации . 88 (422): 520–528. дои : 10.1080/01621459.1993.10476303 . JSTOR 2290332 .
^ Дуонг, Т.; Хейзелтон, МЛ (2003). «Подключаемые матрицы пропускной способности для двумерной оценки плотности ядра». Журнал непараметрической статистики . 15 :17–30. дои : 10.1080/10485250306039 .
^ Ванд, член парламента; Джонс, MC (1994). «Многомерный плагин выбора полосы пропускания». Вычислительная статистика . 9 : 97–177.
^ Jump up to: ^а ^б ^с Дуонг, Т.; Хейзелтон, МЛ (2005). «Матрицы пропускной способности перекрестной проверки для многомерной оценки плотности ядра». Скандинавский статистический журнал . 32 (3): 485–506. дои : 10.1111/j.1467-9469.2005.00445.x .
^ Холл, П.; Маррон, Дж.; Парк, Б. (1992). «Сглаженная перекрестная проверка» . Теория вероятностей и смежные области . 92 : 1–20. дои : 10.1007/BF01205233 .
^ Дуонг, Т.; Хейзелтон, МЛ (2005). «Степень сходимости для селекторов матрицы неограниченной полосы пропускания в многомерной оценке плотности ядра» . Журнал многомерного анализа . 93 (2): 417–433. дои : 10.1016/j.jmva.2004.04.004 .
^ Дуонг, Т. (2007). "ks: Оценка плотности ядра и дискриминантный анализ ядра в R" . Журнал статистического программного обеспечения . 21 (7). дои : 10.18637/jss.v021.i07 .
^ Ботев З.И.; Гротовски, Дж. Ф.; Крозе, Д.П. (2010). «Оценка плотности ядра посредством диффузии». Анналы статистики . 38 (5): 2916–2957. arXiv : 1011.2602 . дои : 10.1214/10-AOS799 .
^ Холл, П.; Ванд, член парламента (1988). «Минимизация _{L 1} расстояния при непараметрической оценке плотности» . Журнал многомерного анализа . 26 : 59–88. дои : 10.1016/0047-259X(88)90073-5 .
^ Цао, Р.; Куэвас, А.; Мантейга, WG (1994). «Сравнительное исследование нескольких методов сглаживания при оценке плотности». Вычислительная статистика и анализ данных . 17 (2): 153–176. дои : 10.1016/0167-9473(92)00066-Z .
^ Холл, П. (1989). «Об оценке потерь и плотности Кульбака-Лейблера» . Анналы статистики . 15 (4): 589–605. дои : 10.1214/aos/1176350606 .
^ Ахмад, Айова; Мугдади, Арканзас (2006). «Взвешенное расстояние Хеллингера как критерий ошибки выбора полосы пропускания при оценке ядра». Журнал непараметрической статистики . 18 (2): 215–226. дои : 10.1080/10485250600712008 .
^ Маррон, Дж. С.; Цыбаков, А. (1996). «Визуальные критерии погрешности качественного сглаживания». Журнал Американской статистической ассоциации . 90 (430): 499–507. дои : 10.2307/2291060 . JSTOR 2291060 .
^ Jump up to: ^а ^б Бернаккья, Альберто; Пиголотти, Симона (01 июня 2011 г.). «Самосогласованный метод оценки плотности». Журнал Королевского статистического общества, серия B. 73 (3): 407–422. arXiv : 0908.3856 . дои : 10.1111/j.1467-9868.2011.00772.x . ISSN 1467-9868 .
^ Jump up to: ^а ^б О'Брайен, Трэвис А.; Коллинз, Уильям Д.; Раушер, Сара А.; Ринглер, Тодд Д. (1 ноября 2014 г.). «Снижение вычислительных затрат ECF с использованием nuFFT: быстрый и объективный метод оценки плотности вероятности» . Вычислительная статистика и анализ данных . 79 : 222–234. дои : 10.1016/j.csda.2014.06.002 .
^ Jump up to: ^а ^б ^с ^д ^и О'Брайен, Трэвис А.; Кашинатх, Картик; Кавано, Николас Р.; Коллинз, Уильям Д.; О'Брайен, Джон П. (2016). «Быстрый и объективный метод многомерной оценки плотности ядра: fastKDE» (PDF) . Вычислительная статистика и анализ данных . 101 : 148–160. дои : 10.1016/j.csda.2016.02.014 .

Внешние ссылки

«Многомерное сглаживание ядра и его применение» — это всеобъемлющая книга по многим темам сглаживания ядра, включая оценку плотности. Включает фрагменты кода пакета в R. ks
kde2d.m Функция Matlab для двумерной оценки плотности ядра.
libagf Библиотека C++ для многомерной оценки плотности ядра с переменной полосой пропускания .
akde.m для M- файл Matlab многомерной оценки плотности ядра с переменной полосой пропускания .
helit и Модуль pyqt_fit.kde в пакете PyQt-Fit — это библиотеки Python для многомерной оценки плотности ядра.

[1] Розенблатт, М. (1956). «Замечания о некоторых непараметрических оценках функции плотности» . Анналы математической статистики . 27 (3): 832–837. дои : 10.1214/aoms/1177728190 .

[2] Парзен, Э. (1962). «Об оценке функции плотности вероятности и режима» . Анналы математической статистики . 33 (3): 1065–1076. дои : 10.1214/aoms/1177704472 .

[WJ1995-3] Jump up to: ^а ^б ^с ^д ^и Ванд, член парламента; Джонс, MC (1995). Сглаживание ядра . Лондон: Чепмен и Холл/CRC. ISBN 9780412552700 .

[simonoff1996-4] Jump up to: ^а ^б Симонов, Дж. С. (1996). Методы сглаживания в статистике . Спрингер. ISBN 9780387947167 .

[chacon2018-5] Чакон, Дж. Э. и Дуонг, Т. (2018). Многомерное ядровое сглаживание и его применение . Чепмен и Холл/CRC. ISBN 9781498763011 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[6] Сильверман, BW (1986). Оценка плотности для статистики и анализа данных . Чепмен и Холл/CRC. стр. 7–11 . ISBN 9780412246203 .

[7] Ванд, член парламента; Джонс, MC (1993). «Сравнение параметризаций сглаживания при двумерной оценке плотности ядра». Журнал Американской статистической ассоциации . 88 (422): 520–528. дои : 10.1080/01621459.1993.10476303 . JSTOR 2290332 .

[DH2003-8] Дуонг, Т.; Хейзелтон, МЛ (2003). «Подключаемые матрицы пропускной способности для двумерной оценки плотности ядра». Журнал непараметрической статистики . 15 :17–30. дои : 10.1080/10485250306039 .

[9] Ванд, член парламента; Джонс, MC (1994). «Многомерный плагин выбора полосы пропускания». Вычислительная статистика . 9 : 97–177.

[DH2005-10] Jump up to: ^а ^б ^с Дуонг, Т.; Хейзелтон, МЛ (2005). «Матрицы пропускной способности перекрестной проверки для многомерной оценки плотности ядра». Скандинавский статистический журнал . 32 (3): 485–506. дои : 10.1111/j.1467-9469.2005.00445.x .

[11] Холл, П.; Маррон, Дж.; Парк, Б. (1992). «Сглаженная перекрестная проверка» . Теория вероятностей и смежные области . 92 : 1–20. дои : 10.1007/BF01205233 .

[12] Дуонг, Т.; Хейзелтон, МЛ (2005). «Степень сходимости для селекторов матрицы неограниченной полосы пропускания в многомерной оценке плотности ядра» . Журнал многомерного анализа . 93 (2): 417–433. дои : 10.1016/j.jmva.2004.04.004 .

[13] Дуонг, Т. (2007). "ks: Оценка плотности ядра и дискриминантный анализ ядра в R" . Журнал статистического программного обеспечения . 21 (7). дои : 10.18637/jss.v021.i07 .

[14] Ботев З.И.; Гротовски, Дж. Ф.; Крозе, Д.П. (2010). «Оценка плотности ядра посредством диффузии». Анналы статистики . 38 (5): 2916–2957. arXiv : 1011.2602 . дои : 10.1214/10-AOS799 .

[15] Холл, П.; Ванд, член парламента (1988). «Минимизация _{L 1} расстояния при непараметрической оценке плотности» . Журнал многомерного анализа . 26 : 59–88. дои : 10.1016/0047-259X(88)90073-5 .

[16] Цао, Р.; Куэвас, А.; Мантейга, WG (1994). «Сравнительное исследование нескольких методов сглаживания при оценке плотности». Вычислительная статистика и анализ данных . 17 (2): 153–176. дои : 10.1016/0167-9473(92)00066-Z .

[17] Холл, П. (1989). «Об оценке потерь и плотности Кульбака-Лейблера» . Анналы статистики . 15 (4): 589–605. дои : 10.1214/aos/1176350606 .

[18] Ахмад, Айова; Мугдади, Арканзас (2006). «Взвешенное расстояние Хеллингера как критерий ошибки выбора полосы пропускания при оценке ядра». Журнал непараметрической статистики . 18 (2): 215–226. дои : 10.1080/10485250600712008 .

[19] Маррон, Дж. С.; Цыбаков, А. (1996). «Визуальные критерии погрешности качественного сглаживания». Журнал Американской статистической ассоциации . 90 (430): 499–507. дои : 10.2307/2291060 . JSTOR 2291060 .

[:0-20] Jump up to: ^а ^б Бернаккья, Альберто; Пиголотти, Симона (01 июня 2011 г.). «Самосогласованный метод оценки плотности». Журнал Королевского статистического общества, серия B. 73 (3): 407–422. arXiv : 0908.3856 . дои : 10.1111/j.1467-9868.2011.00772.x . ISSN 1467-9868 .

[:1-21] Jump up to: ^а ^б О'Брайен, Трэвис А.; Коллинз, Уильям Д.; Раушер, Сара А.; Ринглер, Тодд Д. (1 ноября 2014 г.). «Снижение вычислительных затрат ECF с использованием nuFFT: быстрый и объективный метод оценки плотности вероятности» . Вычислительная статистика и анализ данных . 79 : 222–234. дои : 10.1016/j.csda.2014.06.002 .

[:22-22] Jump up to: ^а ^б ^с ^д ^и О'Брайен, Трэвис А.; Кашинатх, Картик; Кавано, Николас Р.; Коллинз, Уильям Д.; О'Брайен, Джон П. (2016). «Быстрый и объективный метод многомерной оценки плотности ядра: fastKDE» (PDF) . Вычислительная статистика и анализ данных . 101 : 148–160. дои : 10.1016/j.csda.2016.02.014 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]