Формула длины крючка

В комбинаторной математике формула длины крючка представляет собой формулу для числа стандартных таблиц Юнга, форма которых представляет собой заданную диаграмму Юнга .Он имеет приложения в различных областях, таких как теория представлений , вероятность и анализ алгоритмов ; например, проблема длиннейших возрастающих подпоследовательностей . Соответствующая формула дает количество полустандартных таблиц Юнга, которые являются специализацией полинома Шура .

Определения и заявление

Позволять $\lambda =(\lambda _{1}\geq \cdots \geq \lambda _{k})$ быть частью ​ $n=\lambda _{1}+\cdots +\lambda _{k}$.принято интерпретировать $\lambda$ графически как диаграмма Юнга , а именно выровненный по левому краю массив квадратных ячеек с $k$ ряды длин $\lambda _{1},\ldots ,\lambda _{k}$.A (стандартная) Юнга Таблица формы $\lambda$ представляет собой наполнение $n$ ячейки диаграммы Юнга со всеми целыми числами $\{1,\ldots ,n\}$, без повторений, так что каждая строка и каждый столбец образуют возрастающую последовательность.Для ячейки в положении $(i,j)$, в $i$й ряд и $j$столбик, крючок $H_{\lambda }(i,j)$ это набор ячеек $(a,b)$ такой, что $a=i$ и $b\geq j$ или $a\geq i$ и $b=j$.Длина крючка $h_{\lambda }(i,j)$ это количество клеток в $H_{\lambda }(i,j)$.

Формула длины крючка выражает количество стандартных таблиц Юнга формы. $\lambda$, обозначенный $f^{\lambda }$ или $d_{\lambda }$, как

$f^{\lambda }={\frac {n!}{\prod h_{\lambda }(i,j)}},$

где произведение находится по всем ячейкам $(i,j)$ диаграммы Юнга.

Примеры

Таблица, показывающая длину крючка каждой ячейки на диаграмме Янга.
$(4,3,1,1)$

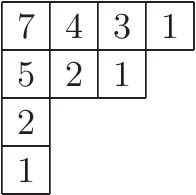
На рисунке справа показаны длины крючков для ячеек на диаграмме Янга. $\lambda =(4,3,1,1)$, что соответствует разбиению 9 = 4 + 3 + 1 + 1. Формула длины крючка дает количество стандартных таблиц Юнга как:

$f^{\lambda }={\frac {9!}{7\cdot 5\cdot 4\cdot 3\cdot 2\cdot 2\cdot 1\cdot 1\cdot 1}}=216.$

Каталонский номер $C_{n}$считает пути Дика с $n$ шаги вверх (U) чередуются с $n$ шаги вниз (D), так что на каждом шаге предшествующих D никогда не бывает больше, чем U. Они находятся в биекции с таблицами формы Янга. $\lambda =(n,n)$: путь Дика соответствует таблице, в первой строке которой указаны положения U-шагов, а во второй строке — позиции D-шагов. Например, UUDDUD соответствует таблицам со строками 125 и 346.

Это показывает, что $C_{n}=f^{(n,n)}$, поэтому формула крючка специализируется на известной формуле произведения

$C_{n}={\frac {(2n)!}{(n+1)(n)\cdots (3)(2)(n)(n-1)\cdots (2)(1)}}={\frac {(2n)!}{(n+1)!\,n!}}={\frac {1}{n{+}1}}{\binom {2n}{n}}.$

История

Есть и другие формулы $f^{\lambda }$, но формула длины крючка особенно проста и элегантна.Менее удобная формула, выражающая $f^{\lambda }$ в терминах определителя был независимо выведен Фробениусом и Янгом в 1900 и 1902 годах соответственно с использованием алгебраических методов. МакМахон нашел альтернативное доказательство формулы Янга-Фробениуса в 1916 году, используя разностные методы.

Сама формула длины крючка была открыта в 1953 году Фреймом, Робинсоном и Траллом как усовершенствование формулы Янга-Фробениуса. Саган описывает это открытие следующим образом.

Однажды в четверг в мае 1953 года Робинсон посетил Фрейма в Мичиганском государственном университете. Обсуждая работу Стаала (ученика Робинсона), Фрейм пришел к выводу о формуле крючка. Сначала Робинсон не мог поверить, что такая простая формула существует, но, попробовав несколько примеров, убедился, и вместе они доказали тождество. В субботу они отправились в Мичиганский университет, где Фрейм представил свой новый результат после лекции Робинсона. Это удивило Тралла, который был в зале, потому что он только что доказал тот же результат в тот же день!

Несмотря на простоту формулы длины крючка, доказательство Фрейма-Робинсона-Тралла не очень проницательно и не дает никакого интуитивного понимания роли крючков. Поиск короткого, интуитивного объяснения, подходящего такому простому результату, привел к появлению множества альтернативных доказательств. Хиллман и Грассл представили первое доказательство, проливающее свет на роль крючков, в 1976 году, доказав особый случай формулы Стэнли о содержании крючка, которая, как известно, подразумевает формулу длины крючка. Грин , Нейенхейс и Уилф нашли вероятностное доказательство, используя метод обхода крючка, в котором длины крючков появляются естественным образом в 1979 году. Реммель адаптировал оригинальное доказательство Фрейма-Робинсона-Тралла в первое биективное доказательство формулы длины крючка в 1982 году. Прямое биективное доказательство было впервые обнаружено Францблау и Зейльбергером в 1982 году. В 1984 году Зейлбергер также преобразовал доказательство ходьбы крюком Грина-Ниенхейса-Уилфа в биективное доказательство. Более простая прямая биекция была анонсирована Паком и Стояновским в 1992 году, а ее полное доказательство было представлено ими и Новелли в 1997 году.

Между тем, формула длины крючка была обобщена несколькими способами.Р.М. Тралл нашел аналог формулы длины крючка для смещенных Таблиц Янга в 1952 году. В 1980 году Саган представил доказательство перемещения смещенного крючка для формулы длины крючка для смещенных таблиц Янга. Саган и Йе доказали формулу длины крюка для бинарных деревьев с помощью обхода крюка в 1989 году. Проктор дал обобщение ЧУМ (см. ниже).

Вероятностное доказательство

Эвристический аргумент Кнута

Формулу длины крючка можно понять интуитивно, используя следующий эвристический, но неверный аргумент, предложенный Д. Е. Кнутом . Учитывая, что каждый элемент таблицы является наименьшим в своем крючке и заполняет форму таблицы случайным образом, вероятность того, что ячейка $(i,j)$ будет содержать минимальный элемент соответствующего крючка, обратный длине крючка. Умножив эти вероятности на все $i$ и $j$ дает формулу. Этот аргумент ошибочен, поскольку события не являются независимыми.

Однако аргумент Кнута верен для перечисления разметок на деревьях, удовлетворяющих свойствам монотонности, аналогичным свойствам таблицы Юнга. В этом случае рассматриваемые события «крючка» на самом деле являются независимыми событиями.

Вероятностное доказательство с использованием обхода крюка

Это вероятностное доказательство, найденное К. Грином , А. Нийенхейсом и Х. С. Уилфом в 1979 году. Определять

$e_{\lambda }={\frac {n!}{\prod _{(i,j)\in Y(\lambda )}h_{\lambda }(i,j)}}.$

Мы хотим показать, что $f^{\lambda }=e_{\lambda }$. Первый,

$f^{\lambda }=\sum _{\mu \uparrow \lambda }f^{\mu },$

Углы диаграммы Юнга (5,3,2,1,1)

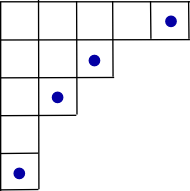
где сумма пробегает все диаграммы Юнга $\mu$ получено от $\lambda$ удалив одну угловую ячейку. (Максимальный вход таблицы Юнга формы $\lambda$ происходит в одной из его угловых ячеек, поэтому его удаление дает таблицу Янга формы $\mu$.)

Мы определяем $f^{\emptyset }=1$и $e_{\emptyset }=1$, поэтому достаточно показать одно и то же повторение

$e_{\lambda }=\sum _{\mu \uparrow \lambda }e_{\mu },$

что подразумевало бы $f^{\lambda }=e_{\lambda }$ по индукции. Приведенную выше сумму можно рассматривать как сумму вероятностей, записав ее как

$\sum _{\mu \uparrow \lambda }{\frac {e_{\mu }}{e_{\lambda }}}=1.$

Поэтому нам нужно показать, что числа ${\frac {e_{\mu }}{e_{\lambda }}}$ определить вероятностную меру на множестве диаграмм Юнга $\mu$ с $\mu \uparrow \lambda$. Это делается конструктивным способом путем определения случайного блуждания, называемого крючковым блужданием , в ячейках диаграммы Юнга. $\lambda$, который в конечном итоге выбирает одну из угловых ячеек $\lambda$ (которые находятся в биекции с диаграммами $\mu$ для чего $\mu \uparrow \lambda$). Ход крюка определяется следующими правилами.

1. Выберите ячейку равномерно случайным образом из $|\lambda |$ клетки. Начните случайное блуждание оттуда.
2. Преемник текущей ячейки $(i,j)$ выбирается равномерно случайным образом от крючка $H_{\lambda }(i,j)\setminus \{(i,j)\}$.
3. Продолжайте, пока не дойдете до угловой ячейки. ${\textbf {c}}$.

Предложение: для данной угловой ячейки $(a,b)$ из $\lambda$, у нас есть

$\mathbb {P} \left({\textbf {c}}=(a,b)\right)={\frac {e_{\mu }}{e_{\lambda }}},$

где $\mu =\lambda \setminus \{(a,b)\}$.

Учитывая это, суммирование по всем угловым ячейкам $(a,b)$ дает $\sum _{\mu \uparrow \lambda }{\frac {e_{\mu }}{e_{\lambda }}}=1$ как заявлено.

Связь с представлениями симметрической группы

Формула длины крючка имеет большое значение в теории представлений симметрической группы. $S_{n}$, где число $f^{\lambda }$ известно, что он равен размерности комплексного неприводимого представления $V_{\lambda }$ связанный с $\lambda$.

Подробное обсуждение

Комплексные неприводимые представления $V_{\lambda }$ симметричной группы индексируются разделами $\lambda$ из $n$ (см. модуль Specht ). Их характеры связаны с теорией симметричных функций через скалярное произведение Холла:

$\chi ^{\lambda }(w)=\langle s_{\lambda },p_{\tau (w)}\rangle ,$

где $s_{\lambda }$ – функция Шура, связанная с $\lambda$ и $p_{\tau (w)}$ - симметричная функция разбиения по сумме степеней $\tau (w)$ связанный с циклическим разложением $w$. Например, если $w=(154)(238)(6)(79)$ затем $\tau (w)=(3,3,2,1)$.

Поскольку тождественная перестановка $e$ имеет форму $e=(1)(2)\cdots (n)$ в обозначениях цикла, $\tau (e)=(1,\ldots ,1)=1^{(n)}$, формула говорит

$f^{\lambda }\,=\,\dim V_{\lambda }\,=\,\chi ^{\lambda }(e)\,=\,\langle s_{\lambda },p_{1^{(n)}}\rangle$

В разложении функций Шура через мономиальные симметричные функции используются числа Костки :

$s_{\lambda }=\sum _{\mu }K_{\lambda \mu }m_{\mu },$

Тогда внутренний продукт с $p_{1^{(n)}}=h_{1^{(n)}}$ является $K_{\lambda 1^{(n)}}$, потому что $\langle m_{\mu },h_{\nu }\rangle =\delta _{\mu \nu }$. Обратите внимание, что $K_{\lambda 1^{(n)}}$ равно $f^{\lambda }=\dim V_{\lambda }$, так что $\textstyle \sum _{\lambda \vdash n}\left(f^{\lambda }\right)^{2}=n!$ от рассмотрения регулярного представительства $S_{n}$или комбинаторно из соответствия Робинсона-Шенстеда-Кнута .

Расчет также показывает, что:

$(x_{1}+x_{2}+\cdots +x_{k})^{n}=\sum _{\lambda \vdash n}s_{\lambda }f^{\lambda }.$

Это расширение $p_{1^{(n)}}$ в терминах функций Шура с использованием коэффициентов, заданных внутренним произведением, поскольку $\langle s_{\mu },s_{\nu }\rangle =\delta _{\mu \nu }$.Вышеупомянутое равенство можно доказать, также проверив коэффициенты каждого монома с обеих сторон и используя соответствие Робинсона-Шенстеда-Кнута или, более концептуально, рассматривая разложение $V^{\otimes n}$ по неприводимому $GL(V)$ модули и прием персонажей. См. двойственность Шура – ​​Вейля .

Доказательство формулы крючка с использованием формулы Фробениуса

Источник:

По вышеизложенным соображениям

$p_{1^{(n)}}=\sum _{\lambda \vdash n}s_{\lambda }f^{\lambda }$

так что

$\Delta (x)p_{1^{(n)}}=\sum _{\lambda \vdash n}\Delta (x)s_{\lambda }f^{\lambda }$

где $\Delta (x)=\prod _{i<j}(x_{i}-x_{j})$ – определитель Вандермонда .

Для раздела $\lambda =(\lambda _{1}\geq \cdots \geq \lambda _{k})$, определять $l_{i}=\lambda _{i}+k-i$ для $i=1,\ldots ,k$. Для дальнейшего нам нужно как минимум столько же переменных, сколько строк в разделе, поэтому с этого момента мы работаем с $n$ переменные $x_{1},\cdots ,x_{n}$.

Каждый термин $\Delta (x)s_{\lambda }$ равно

$a_{(\lambda _{1}+k-1,\lambda _{2}+k-2,\dots ,\lambda _{k})}(x_{1},x_{2},\dots ,x_{k})\ =\ \det \!\left[{\begin{matrix}x_{1}^{l_{1}}&x_{2}^{l_{1}}&\dots &x_{k}^{l_{1}}\\x_{1}^{l_{2}}&x_{2}^{l_{2}}&\dots &x_{k}^{l_{2}}\\\vdots &\vdots &\ddots &\vdots \\x_{1}^{l_{k}}&x_{2}^{l_{k}}&\dots &x_{k}^{l_{k}}\end{matrix}}\right]$

(См. функцию Шура .) Поскольку вектор $(l_{1},\ldots ,l_{k})$ различен для каждого раздела, это означает, что коэффициент $x_{1}^{l_{1}}\cdots x_{k}^{l_{k}}$ в $\Delta (x)p_{1^{(n)}}$, обозначенный $\left[\Delta (x)p_{1^{(n)}}\right]_{l_{1},\cdots ,l_{k}}$, равно $f^{\lambda }$. Это известно как формула характера Фробениуса , которая дает одно из самых ранних доказательств.

Осталось только упростить этот коэффициент. Умножение

$\Delta (x)\ =\ \sum _{w\in S_{n}}\operatorname {sgn}(w)x_{1}^{w(1)-1}x_{2}^{w(2)-1}\cdots x_{k}^{w(k)-1}$

и

$p_{1^{(n)}}\ =\ (x_{1}+x_{2}+\cdots +x_{k})^{n}\ =\ \sum {\frac {n!}{d_{1}!d_{2}!\cdots d_{k}!}}x_{1}^{d_{1}}x_{2}^{d_{2}}\cdots x_{k}^{d_{k}}$

мы заключаем, что наш коэффициент как

$\sum _{w\in S_{n}}\operatorname {sgn}(w){\frac {n!}{(l_{1}-w(1)+1)!\cdots (l_{k}-w(k)+1)!}}$

который можно записать как

${\frac {n!}{l_{1}!l_{2}!\cdots l_{k}!}}\sum _{w\in S_{n}}\operatorname {sgn}(w)\left[(l_{1})(l_{1}-1)\cdots (l_{1}-w(1)+2)\right]\left[(l_{2})(l_{2}-1)\cdots (l_{2}-w(2)+2)\right]\left[(l_{k})(l_{k}-1)\cdots (l_{k}-w(k)+2)\right]$

Последняя сумма равна следующему определителю

$\det \left[{\begin{matrix}1&l_{1}&l_{1}(l_{1}-1)&\dots &\prod _{i=0}^{k-2}(l_{1}-i)\\1&l_{2}&l_{2}(l_{2}-1)&\dots &\prod _{i=0}^{k-2}(l_{2}-i)\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&l_{k}&l_{k}(l_{k}-1)&\dots &\prod _{i=0}^{k-2}(l_{k}-i)\end{matrix}}\right]$

который по столбцу сводится к определителю Вандермонда , и мы получаем формулу

$f^{\lambda }={\frac {n!}{l_{1}!\,l_{2}!\cdots l_{k}!}}\prod _{i<j}(l_{i}-l_{j}).$

Обратите внимание, что $l_{i}$ — длина крючка первого ящика в каждой строке диаграммы Юнга, и это выражение легко преобразуется к желаемому виду ${\frac {n!}{\prod h_{\lambda }(i,j)}}$: один показывает $\textstyle l_{i}!=\prod _{j>i}(l_{i}-l_{j})\cdot \prod _{j\leq \lambda _{i}}h_{\lambda }(i,j)$, где последнее произведение пробегает $i$четвертая строка диаграммы Юнга.

Связь с самыми длинными возрастающими подпоследовательностями

Формула длины крюка также имеет важные приложения для анализа самых длинных возрастающих подпоследовательностей в случайных перестановках. Если $\sigma _{n}$ обозначает равномерно случайную перестановку порядка $n$, $L(\sigma _{n})$ обозначает максимальную длину возрастающей подпоследовательности $\sigma _{n}$, и $\ell _{n}$ обозначает ожидаемое (среднее) значение $L(\sigma _{n})$, Anatoly Vershik and Sergei Kerov и независимо Бенджамин Ф. Логан и Лоуренс А. Шепп показал, что когда $n$ большой, $\ell _{n}$ приблизительно равно $2{\sqrt {n}}$. Это ответ на вопрос, первоначально заданный Станиславом Уламом . Доказательство основано на переводе вопроса через соответствие Робинсона–Шенстеда на задачу о предельной форме случайной таблицы Юнга, выбранной по мере Планшереля . Поскольку в определение меры Планшереля входит величина $f^{\lambda }$, формулу длины крюка затем можно использовать для выполнения асимптотического анализа предельной формы и тем самым также ответить на исходный вопрос.

Идеи Вершика-Керова и Логана-Шеппа позже были уточнены Джинхо Байком, Перси Дейфтом и Куртом Йоханссоном, которые смогли добиться гораздо более точного анализа предельного поведения максимальной возрастающей длины подпоследовательности, доказав важный результат, известный сейчас. как теорема Байка–Дейфта–Йоханссона. В их анализе вновь решающим образом используется тот факт, что $f^{\lambda }$ имеет ряд хороших формул, хотя вместо формулы длины крючка использовалось одно из определяющих выражений.

Связанные формулы

Формула количества таблиц Юнга формы $\lambda$ первоначально был получен из формулы определителя Фробениуса в связи с теорией представлений:

$f(\lambda _{1},\ldots ,\lambda _{k})={\frac {n!\,\Delta (\lambda _{k},\lambda _{k-1}+1,\ldots ,\lambda _{1}+k-1)}{\lambda _{k}!\,(\lambda _{k-1}+1)!\cdots (\lambda _{1}+k-1)!}}.$

Длины крюков также могут использоваться для представления произведения производящей функции для количества обратных плоских перегородок заданной формы. Если λ является разбиением некоторого целого числа p , обратное плоское разбиение n формы λ получается путем заполнения полей в диаграмме Юнга неотрицательными целыми числами, так что записи добавляются к n и не уменьшаются вдоль каждой строки. и вниз по каждому столбцу. Длина крючка $h_{1},\dots ,h_{p}$ можно определить как с таблицами Юнга. Если π _n обозначает количество обратных плоских разбиений n формы λ , то производящую функцию можно записать как

$\sum _{n=0}^{\infty }\pi _{n}x^{n}=\prod _{k=1}^{p}(1-x^{h_{k}})^{-1}$

Стэнли открыл другую формулу для той же производящей функции. В общем, если $A$ какое-нибудь частичное множество с $n$ элементы, производящая функция для обратного $A$-разделы

${\frac {P(x)}{(1-x)(1-x^{2})\cdots (1-x^{n})}}$

где $P(x)$ является полиномом таким, что $P(1)$ количество расширений линейных $A$.

В случае перегородки $\lambda$, мы рассматриваем ЧУМ в его ячейках, заданных соотношением

$(i,j)\leq (i',j')\iff i\leq i'\qquad {\textrm {and}}\qquad j\leq j'$.

Таким образом, линейное расширение — это просто стандартная таблица Юнга, т.е. $P(1)=f^{\lambda }$

Доказательство формулы крючка с использованием формулы Стэнли.

Объединив две формулы для производящих функций, имеем

${\frac {P(x)}{(1-x)(1-x^{2})\cdots (1-x^{n})}}=\prod _{(i,j)\in \lambda }(1-x^{h_{(i,j)}})^{-1}$

Обе стороны сходятся внутри диска радиуса один, и для $|x|<1$

$P(x)={\frac {\prod _{k=1}^{n}(1-x^{k})}{\prod _{(i,j)\in \lambda }(1-x^{h_{(i,j)}})}}.$

Было бы жестоко вставлять 1, но правая часть представляет собой непрерывную функцию внутри единичного круга, а полином непрерывен везде, так что, по крайней мере, мы можем сказать

$P(1)=\lim _{x\to 1}{\frac {\prod _{k=1}^{n}(1-x^{k})}{\prod _{(i,j)\in \lambda }(1-x^{h_{(i,j)}})}}.$

Применение правила Лопиталя $n$ раз дает формулу длины крючка

$P(1)={\frac {n!}{\prod _{(i,j)\in \lambda }h_{(i,j)}}}.$

Полустандартная формула длины крючка для таблиц

Шура Полином $s_{\lambda }(x_{1},\ldots ,x_{k})$ – производящая функция полустандартных таблиц Юнга формы $\lambda$ и записи в $\{1,\ldots ,k\}$. Специализируясь на этом $x_{i}=1$ дает количество полустандартных таблиц, которые можно записать через длину крючка:

$s_{\lambda }(1,\ldots ,1)\ =\ \prod _{(i,j)\in \mathrm {Y} (\lambda )}{\frac {k-i+j}{h_{\lambda }(i,j)}}.$

Диаграмма Янга $\lambda$ соответствует неприводимому представлению специальной линейной группы $\mathrm {SL} _{k}(\mathbb {C} )$, а полином Шура также является характером диагональной матрицы $\mathrm {diag} (x_{1},\ldots ,x_{k})$ действуя по этому представлению. Таким образом, указанная выше специализация является размерностью неприводимого представления, а формула является альтернативой более общей формуле размерности Вейля .

Мы можем уточнить это, взяв основную специализацию функции Шура в переменных $1,t,t^{2}\!,t^{3}\!,\ldots$ :

$s_{\lambda }(1,t,t^{2},\ldots )\ =\ {\frac {t^{n\left(\lambda \right)}}{\prod _{(i,j)\in Y(\lambda )}(1-t^{h_{\lambda }(i,j)})}},$

где $n(\lambda )=\sum _{i}(i{-}1)\lambda _{i}=\sum _{i}{\tbinom {\lambda _{i}'}{2}}$ для сопряженного раздела $\lambda '$.

Формула наклонной формы

Существует обобщение этой формулы для косых форм:

$s_{\lambda /\mu }(1,t,t^{2},\cdots )=\sum _{S\in E(\lambda /\mu )}\prod _{(i,j)\in \lambda \setminus S}{\frac {t^{\lambda _{j}'-i}}{1-t^{h(i,j)}}}$

где сумма берется по возбужденным диаграммам вида $\lambda$ и коробки распределяются согласно $\mu$.

Вариацию на ту же тему дают Окуньков и Ольшанский. формы

${\frac {\dim \lambda /\mu }{\dim \lambda }}={\frac {s_{\mu }^{*}(\lambda )}{|\lambda |!/|\mu |!}},$

где $s_{\mu }^{*}$ это так называемая сдвинутая функция Шура $s_{\mu }^{*}(x_{1},\dots ,x_{n})={\frac {\det[(x_{i}+n-1)!/(\mu _{j}+n-j)!]}{\det[(x_{i}+n-i)!/(n-j)!]}}$.

Обобщение до d -полных частично упорядоченных множеств

Диаграммы Юнга можно рассматривать как идеалы конечного порядка в частично упорядоченном множестве $\mathbb {N} \times \mathbb {N}$, а стандартные таблицы Юнга являются их линейными расширениями . Роберт Проктор дал обобщение формулы длины крюка для подсчета линейных расширений более широкого класса ЧУМ, обобщающих как деревья, так и косые диаграммы.

Внешние ссылки

• «Удивительная математика самых длинных возрастающих подпоследовательностей» Дэна Ромика. Содержит обсуждение формулы длины крюка и нескольких ее вариантов с приложениями к математике самых длинных возрастающих подпоследовательностей.