м -арное дерево

Пример m-арного дерева с m=5

В теории графов m - арное дерево (для неотрицательных целых чисел m ) (также известное как n -арное , k -арное или k -образное дерево) является древовидным деревом (или, по мнению некоторых авторов, упорядоченным деревом ). в котором каждый узел имеет не более m детей. Бинарное дерево — важный случай, когда m = 2; аналогично троичным деревом является дерево, в котором m = 3.

Виды м -арных деревьев

• Полное m m -арное дерево — это m -арное дерево, в котором на каждом уровне каждый узел имеет 0 или дочерних элементов.
• Полное м - арное дерево (или, реже, совершенное м -арное дерево ) — полное m -арное дерево, в котором все листовые узлы находятся на одной глубине.

Свойства м -арных деревьев

• Для m -арного дерева высотой h верхняя граница максимального количества листьев равна $m^{h}$.
• Высота h - арного m дерева не включает корневой узел, при этом дерево содержит только корневой узел, имеющий высоту 0.
• Высота дерева равна максимальной глубине D любого узла дерева.
• Общее количество узлов $N$ в полном m -арном дереве есть ${\textstyle \sum _{i=0}^{h}m^{i}={\frac {m^{h+1}-1}{m-1}}}$, а высота h равна

$${\begin{aligned}&{\frac {m^{h+1}-1}{m-1}}\geq N>{\frac {m^{h}-1}{m-1}}\\[8pt]&m^{h+1}\geq (m-1)\cdot N+1>m^{h}\\[8pt]&h+1\geq \log _{m}\left((m-1)\cdot N+1\right)>h\\[8pt]&h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil .\end{aligned}}$$ По определению Big-Ω максимальная глубина $$D=h\geq \left\lceil \log _{m}((m-1)\cdot N+1)-1\right\rceil =O(\log _{m}n)=O(\log n/\log m).$$

• Высота полного m -арного дерева с n узлами равна ${\textstyle \lfloor \log _{m}((m-1)\cdot n)\rfloor }$.
• Общее количество возможных m -арных деревьев с n узлами равно ${\textstyle C_{n}={\frac {1}{(m-1)n+1}}\cdot {\binom {m\cdot n}{n}}}$ (это каталонский номер ).

Методы обхода m- арных деревьев

Основная статья: обход дерева

Обход m -арного дерева очень похож на обход бинарного дерева. Обход в предварительном порядке идет к родительскому, левому поддереву и правому поддереву, а для обхода после порядка он идет через левое поддерево, правое поддерево и родительский узел. Для обхода по порядку, поскольку на узел приходится более двух потомков при m > 2 , необходимо определить понятие левого и правого поддеревьев. Один из распространенных методов создания левых/правых поддеревьев — разделить список дочерних узлов на две группы. Определив порядок для m дочерних узлов узла, первый ${\textstyle \{1,\dots ,\lfloor {\frac {m}{2}}\rfloor \}}$ узлы будут составлять левое поддерево и ${\textstyle \{\lceil {\frac {m}{2}}\rceil ,\dots ,m\}}$ узлы будут составлять правильное поддерево.

Преобразование m -арного дерева в двоичное дерево

Пример преобразования m-арного дерева в бинарное дерево. м=6

Использование массива для представления m -дерева неэффективно, поскольку большинство узлов в практических приложениях содержат менее m дочерних узлов. В результате этот факт приводит к разреженному массиву с большим неиспользуемым пространством в памяти. Преобразование произвольного m- дерева в двоичное дерево только увеличит высоту дерева в постоянный коэффициент и не повлияет на общую временную сложность в худшем случае. Другими словами, ${\textstyle O(\log _{m}n)\equiv O(\log _{2}n)}$ с ${\textstyle \log _{2}m\cdot \log _{m}n={\frac {\log m}{\log 2}}\cdot {\frac {\log n}{\log m}}=\log _{2}n}$.

Сначала мы связываем все непосредственные дочерние узлы данного родительского узла вместе, чтобы сформировать список связей. Затем мы сохраняем ссылку от родителя на первого (т. е. самого левого) дочернего элемента и удаляем все остальные ссылки на остальных дочерних элементов. Мы повторяем этот процесс для всех детей (если у них есть дети), пока не обработаем все внутренние узлы и не повернём дерево на 45 градусов по часовой стрелке. Полученное дерево является искомым бинарным деревом, полученным из заданного m -арного дерева.

Методы хранения м -арных деревьев

Массивы

Пример хранения m-арного дерева с m=3 в массиве

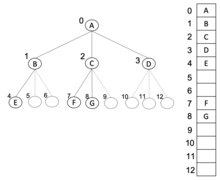
m -арные деревья также могут храниться в порядке ширины как неявная структура данных в массивах , и если дерево является полным m -арным деревом, этот метод не теряет места. В этом компактном расположении, если узел имеет индекс i , его c -й дочерний элемент в диапазоне {1,…, m } находится по индексу $m\cdot i+c$, а его родительский элемент (если есть) находится по индексу ${\textstyle \left\lfloor {\frac {i-1}{m}}\right\rfloor }$ (при условии, что корень имеет нулевой индекс, что означает массив, отсчитываемый от 0). Этот метод выигрывает от более компактного хранения и лучшей локальности ссылок , особенно во время обхода предварительного заказа. Пространственная сложность этого метода $O(m^{n})$.

На основе указателя

Каждый узел будет иметь внутренний массив для хранения указателей на каждый из его узлов. $m$ дети:

Реализация m-арного дерева на основе указателей, где m =4.

По сравнению с реализацией на основе массива, этот метод реализации имеет более высокую пространственную сложность: $O(m\cdot n)$.

Перечень м- рых деревьев

Основная статья: Перечислительная комбинаторика

Перечисление всех возможных m -арных деревьев полезно во многих дисциплинах как способ проверки гипотез и теорий.Правильное представление объектов mary- дерева может значительно упростить процесс генерации. Можно построить представление битовой последовательности, используя поиск в глубину m -арного дерева с n узлами, указывающими наличие узла по заданному индексу с использованием двоичных значений. Например, битовая последовательность x=1110000100010001000 представляет собой трехмерное дерево с n=6 узлами, как показано ниже.

3-ary tree with bit sequence of 1110000100010001000 and Simple Zero Sequence of 004433

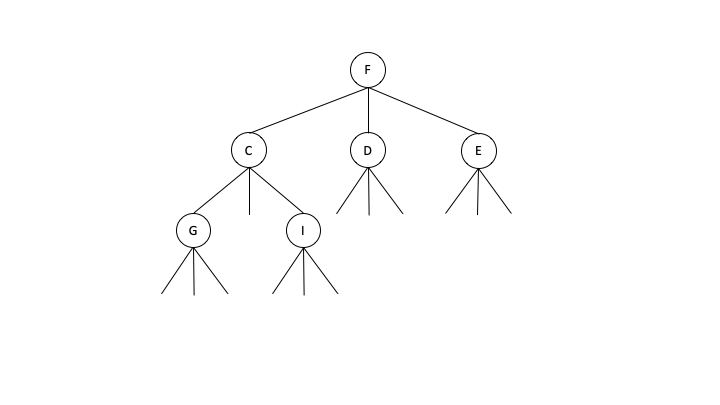
Проблема с этим представлением заключается в том, что перечисление всех битовых строк в лексикографическом порядке будет означать, что две последовательные строки могут представлять два дерева, которые лексикографически сильно различаются. Следовательно, перечисление двоичных строк не обязательно приведет к упорядоченной генерации всех m- мерных деревьев. Лучшее представление основано на целочисленной строке, которая указывает количество нулей между последовательными единицами, известной как Простая Нулевая Последовательность . ${\textstyle S=s_{1},s_{2},\dots ,s_{n-1}}$ — это простая нулевая последовательность, соответствующая битовой последовательности ${\textstyle 10^{s_{1}}10^{s_{2}}\ldots 10^{s_{n-1}}10^{j}}$ где j — количество нулей, необходимое в конце последовательности, чтобы строка имела подходящую длину. Например, $1110000100010001000\equiv 10^{0}10^{0}10^{4}10^{4}10^{3}\equiv 00433$ — это простое представление нулевой последовательности, представленное на рисунке выше. Более компактное представление 00433 : $0^{2}4^{1}3^{2}$, которая называется нулевой последовательностью , в которой повторяющиеся основания не могут быть соседними. Это новое представление позволяет построить следующую действительную последовательность в $O(1)$.Простая нулевая последовательность действительна, если $$\sum _{i=1}^{i=j}s_{i}\leq (m-1)j\qquad \forall j\leq n-1.$$То есть количество нулей в битовой последовательности m -арного дерева не может превышать общее количество нулевых указателей (т. е. указателей без прикрепленных к ним дочерних узлов). Это суммирование накладывает ограничение на $n-1$ узлов, чтобы было место для добавления $n^{t}h$ без создания недопустимой структуры (т. е. наличия доступного нулевого указателя для прикрепления к ней последнего узла).

В таблице ниже показан список всех допустимых простых нулевых последовательностей всех 3 -арных деревьев с 4 узлами:

222	200	111	033	013
221	132	110	032	012
220	131	105	031	011
213	130	104	030	010
212	123	103	024	006
211	122	102	023	005
210	121	101	022	004
204	120	100	021	003
203	114	042	020	002
202	113	041	015	001
201	112	040	014	000

Начиная с нижнего правого угла таблицы (т. е. «000»), существует базовый шаблон , который управляет генерацией возможных упорядоченных деревьев, начиная с «000» до «006». Шаблон магистрали для этой группы («00X») изображен ниже, где дополнительный узел добавляется в позиции, помеченные «x».

Как только будут исчерпаны все возможные позиции в шаблоне магистрали, новый шаблон будет создан путем смещения третьего узла на одну позицию вправо, как показано ниже, и такое же перечисление будет происходить до тех пор, пока не будут исчерпаны все возможные позиции, помеченные «X».

Возвращаясь к таблице перечисления всех m -арных деревьев, где $m=3$ и $n=4$, мы можем легко наблюдать очевидный скачок с «006» на «010», который можно объяснить тривиально алгоритмически, как показано ниже:

Псевдокод этого перечисления приведен ниже:

Procedure NEXT(s1, s2, …, sn−1)    if si = 0 for all i then        finished    else        i ← max {i | si > 0}        si ← si − 1        if i < n − 1 then            si ← (i + 1) ⋅ (m − 1) − sum(sj)        end if        for j ← i + 2, i + 3, …, n − 1            sj ← k − 1    end ifend

Бесцикловое перечисление

Алгоритм генерации, который принимает $O(1)$ время в худшем случае называется безцикловым, поскольку временная сложность не может включать цикл или рекурсию. Бесцикловый перебор m- арных деревьев называется бесцикловым, если после инициализации он генерирует последовательные объекты дерева в $O(1)$. Для данного m- арного дерева T с $a$ являясь одним из его узлов и $d$ его $t$-й ребенок, поворот влево на $a$ делается путем создания $d$ корневой узел и создание $b$ и все его поддеревья являются потомками $a$, дополнительно мы присваиваем $m-1$ оставил большинство детей $d$ к $a$ и самый правый ребенок $d$ остается привязанным к нему, пока $d$ получает root-права, как показано ниже:

Convert an m-ary tree to left-tree    for i = 1...n:         for t = 2...m:             while t child of node at depth i ≠ 1:                L-t rotation at nodes at depth i              end while          end for     end for

Поворот вправо в точке d является обратной этой операции. Левая цепочка T представляет собой последовательность $x_{1},x_{2},\dots ,x_{n}$ узлы такие, что $x_{1}$ является корнем и всеми узлами, кроме $x_{n}$ иметь одного ребенка, подключенного к самому левому краю (т. е. $m[1]$) указатель. Любое m- арное дерево можно преобразовать в дерево левой цепи , используя последовательность конечных вращений влево-t для t от 2 до m . В частности, это можно сделать, выполняя повороты влево на каждом узле. $x_{i}$ пока все это $m-1$ поддерево становится нулевым на каждой глубине. Затем последовательность количества поворотов влево-t, выполненных на глубине i, обозначается $c_{i}$ определяет кодовое слово m - арного дерева, которое можно восстановить, выполнив ту же последовательность поворотов вправо-t.

Пусть $m-1$ кортеж из $c_{1},c_{2},\dots ,c_{m-1}$ представляют количество вращений L-2 , вращений L-3 , ..., вращений Lm , произошедших в корне (т. е. i = 1). Затем $c_{(i-1)(m-1)+t-1}$ — количество вращений Lt, необходимое на глубине i .

Регистрация количества поворотов влево на каждой глубине — это способ кодирования m -арного дерева. Таким образом, перечисление всех возможных допустимых кодировок поможет нам сгенерировать все m -арные деревья для заданных m и n . Но не все $c_{i}$ последовательности m неотрицательных целых чисел представляют собой допустимое m-арное дерево. Последовательность $(n-1)\cdot (m-1)+1$ неотрицательные целые числа являются допустимым представлением m- арного дерева тогда и только тогда, когда $$\sum _{i=j}^{n}\sum _{t=2}^{m}c_{(i-1)(m-1)+t-1}\qquad \leq n-j,\qquad \forall j\in 0\dots n.$$

Лексикографически наименьшее представление кодового слова m-арного числа с n узлами представляет собой все нули, а наибольшее - это n -1 единиц, за следует m которыми справа -1 нуль.

Initialization    c[i] to zero for all i from 1 to n⋅(k − 1)    p[i] set to n − 1 for i from 1 to n    sum ← 0    j ← m − 1Termination Condition    Terminate when c[1] = n − 1Procedure NEXT    sum ← sum + 1 − c[j + 1]    c[j] ← c[j] + 1    if p[q[j]] > p[q[j + 1]] + 1 then        p[q[j]] ← p[q[j + 1]] + 1    end if    p[q[j + c[j]]] ← p[q[j]]    c[j + 1] ← 0    if sum = p[q[j]] then        j ← j − 1    else        p[n] ← sum        j ← m − 1    end ifend

Приложение

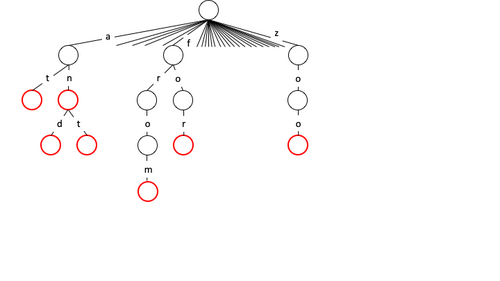
Одним из применений m -арного дерева является создание словаря для проверки допустимых строк. Для этого пусть m будет равно количеству допустимых алфавитов (например, количеству букв английского алфавита ) с корнем дерева, представляющим начальную точку. Аналогично, каждый из дочерних элементов может иметь до m дочерних элементов, представляющих следующий возможный символ в строке. Таким образом, символы вдоль путей могут представлять действительные ключи, отмечая конечный символ ключей как «конечный узел». Например, в примере ниже «at» и «and» являются допустимыми ключевыми строками, где «t» и «d» отмечены как конечные узлы. Терминальные узлы могут хранить дополнительную информацию, которая будет связана с данным ключом. Существуют аналогичные способы создания такого словаря с использованием B-tree , Octree и/или trie .

См. также

• Фактор разветвления
• Бинарное дерево левого дочернего элемента и правого родственного элемента
• Бинарное дерево

Ссылки

• Сторер, Джеймс А. (2001). Введение в структуры данных и алгоритмы . Биркхойзер Бостон. ISBN  3-7643-4253-6 .

Внешние ссылки

• N -арные деревья, Бруно Р. Прейсс, доктор философии, профессор технических наук.