Квантовый граф

Эта статья о метрических графах, оснащенных дифференциальным оператором. Информацию о квантовых состояниях, представленных графиками, см. в разделе Состояние графика .

В математике и физике квантовый граф — это линейная сетевая структура вершин, соединенных по ребрам (т. е. граф ), в которой каждому ребру задана длина и где на каждом из них ставится дифференциальное (или псевдодифференциальное) уравнение. край. Примером может служить электросеть, состоящая из линий электропередач (ребер), соединенных на трансформаторных подстанциях (вершинах); дифференциальные уравнения затем будут описывать напряжение вдоль каждой из линий с граничными условиями для каждого ребра, предусмотренными в соседних вершинах, гарантируя, что ток, добавляемый по всем ребрам, будет равен нулю в каждой вершине.

Квантовые графы были впервые изучены Лайнусом Полингом как модели свободных электронов в органических молекулах в 1930-х годах. Они также возникают в различных математических контекстах, например, в качестве модельных систем в квантовом хаосе , при изучении волноводов , в фотонных кристаллах и в локализации Андерсона , или в качестве ограничения на усадку тонких проводов. Квантовые графы стали известными моделями в мезоскопической физике, используемыми для теоретического понимания нанотехнологий . Другое, более простое понятие квантовых графов было введено Фридманом и др.

Помимо фактического решения дифференциальных уравнений, представленных на квантовом графе, для целей конкретных приложений, типичными вопросами, которые возникают, являются вопросы управляемости (какие входные данные необходимо предоставить, чтобы привести систему в желаемое состояние, например, обеспечить достаточную мощность для всех домов). в электросети) и идентифицируемость (как и где нужно что-то измерить, чтобы получить полную картину состояния системы, например, измерить давление в водопроводной сети, чтобы определить, есть ли протечка в трубе).

Метрические графики

Метрический граф, вложенный в плоскость с тремя открытыми ребрами. Пунктирная линия обозначает метрическое расстояние между двумя точками. $x$ и $y$.

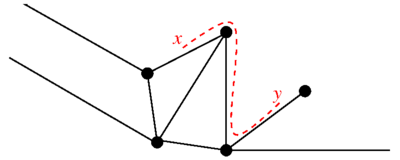
Метрический график – это граф , состоящий из множества $V$ вершин и набор $E$ ребер, где каждое ребро $e=(v_{1},v_{2})\in E$ был связан с интервалом $[0,L_{e}]$ так что $x_{e}$ это координата на интервал, вершина $v_{1}$ соответствует $x_{e}=0$ и $v_{2}$ к $x_{e}=L_{e}$ или наоборот. Выбор того, какая вершина лежит в нуле, произвольным с альтернативой, соответствующей замене координаты на край.Граф имеет естественную метрику: для двух очки $x,y$ на графике, $\rho (x,y)$ является кратчайшее расстояние между нимигде расстояние измеряется по краям графа.

Открытые графы: в модели комбинаторных графов ребра всегда соединяют пары вершин, однако в квантовом графе можно также рассмотрим полубесконечные ребра. Это ребра, связанные с интервалом $[0,\infty )$ прикреплен к одной вершине в $x_{e}=0$. График с одним или несколькими такие открытые ребра называются открытым графом.

Квантовые графики

Квантовые графы — это метрические графы, снабженные дифференциальным (или псевдодифференциальный ) оператор, действующий на функции на графике. Функция $f$ на метрическом графе определяется как $|E|$-кортеж функций $f_{e}(x_{e})$ на интервалах. Гильбертово пространство графа есть $\bigoplus _{e\in E}L^{2}([0,L_{e}])$где внутренний продукт двух функций равен

$\langle f,g\rangle =\sum _{e\in E}\int _{0}^{L_{e}}f_{e}^{*}(x_{e})g_{e}(x_{e})\,dx_{e},$

$L_{e}$ может быть бесконечным в случае открытого края. Простейшим примером оператора на метрическом графе является оператор Лапласа . Оператор на ребре $-{\frac {{\textrm {d}}^{2}}{{\textrm {d}}x_{e}^{2}}}$ где $x_{e}$ это координата на ребре. Чтобы сделать оператор самосопряженным, необходимо указать подходящий домен. Обычно это достигается использованием пространства Соболева $H^{2}$ функций на ребрах графа и задание условий совмещения в вершинах.

Тривиальным примером условий сшивки, которые делают оператор самосопряженным, являются граничные условия Дирихле : $f_{e}(0)=f_{e}(L_{e})=0$ для каждого края. Собственную функцию на конечном ребре можно записать как

$f_{e}(x_{e})=\sin \left({\frac {n\pi x_{e}}{L_{e}}}\right)$

для целого числа $n$. Если граф замкнут и не имеет бесконечных ребер и длины ребер графа рационально независимытогда собственная функция поддерживается на одном ребре графа а собственные значения ${\frac {n^{2}\pi ^{2}}{L_{e}^{2}}}$. Условия Дирихле не допускайте взаимодействия между интервалами, чтобы спектр был таким же, как множество несвязных ребер.

Более интересными условиями самосопряженного совмещения, которые допускают взаимодействие между ребрами, являются условия Неймана или естественные условия совмещения. Функция $f$ в области определения оператор непрерывен всюду на графике и сумма исходящих производных в вершине равна нулю,

$\sum _{e\sim v}f'(v)=0\ ,$

где $f'(v)=f'(0)$ если вершина $v$ находится в $x=0$ и $f'(v)=-f'(L_{e})$ если $v$ находится в $x=L_{e}$.

Изучены также свойства других операторов на метрических графах.

• К ним относятся более общий класс операторов Шредингера:

$\left(i{\frac {\textrm {d}}{{\textrm {d}}x_{e}}}+A_{e}(x_{e})\right)^{2}+V_{e}(x_{e})\ ,$

где $A_{e}$ представляет собой «магнитный векторный потенциал» на краю и $V_{e}$ является скалярным потенциалом.

• Другим примером является оператор Дирака на графике, который представляет собой матричный оператор, действующий на векторные функции, описывающие квантовую механику частиц с собственным угловым моментом, равным половине, таких как электрон .
• Оператор Дирихле-Неймана на графе — это псевдодифференциальный оператор, возникающий при изучении фотонных кристаллов .

Теоремы

Все условия самосопряженного совмещения оператора Лапласа на графе можно классифицировать по схеме Кострыкина и Шредера. На практике зачастую удобнее принять формализм, введенный Кучментом, см. что автоматически дает оператор в вариационной форме.

Позволять $v$ быть вершиной с $d$ края, исходящие из него. Для простоты выберем координаты на ребрах так, чтобы $v$ лежит в $x_{e}=0$ за каждую краевую встречу в $v$. Для функции $f$ на графике пусть

$\mathbf {f} =(f_{e_{1}}(0),f_{e_{2}}(0),\dots ,f_{e_{d}}(0))^{T},\qquad \mathbf {f} '=(f'_{e_{1}}(0),f'_{e_{2}}(0),\dots ,f'_{e_{d}}(0))^{T}.$

Условия соответствия на $v$ может быть задано парой матриц $A$ и $B$ через линейное уравнение,

$A\mathbf {f} +B\mathbf {f} '=\mathbf {0} .$

Условия соответствия определяют самосопряженный оператор, если $(A,B)$ имеет максимальный ранг $d$ и $AB^{*}=BA^{*}.$

Спектр оператора Лапласа на конечном графе удобно описать используя подход матрицы рассеяния, предложенный Коттосом и Смилански. Проблема собственных значений на ребре такова:

$-{\frac {d^{2}}{dx_{e}^{2}}}f_{e}(x_{e})=k^{2}f_{e}(x_{e}).\,$

Таким образом, решение на ребре можно записать как линейную комбинацию плоских волн .

$f_{e}(x_{e})=c_{e}{\textrm {e}}^{ikx_{e}}+{\hat {c}}_{e}{\textrm {e}}^{-ikx_{e}}.\,$

где в нестационарном уравнении Шредингера $c$ коэффициент исходящей плоской волны при $0$ и ${\hat {c}}$ коэффициент входящего плоская волна в $0$.Условия соответствия при $v$ определить матрицу рассеяния

$S(k)=-(A+ikB)^{-1}(A-ikB).\,$

Матрица рассеяния связывает векторы приходящей и уходящей плоской волны коэффициенты при $v$, $\mathbf {c} =S(k){\hat {\mathbf {c} }}$.Для условий самосопряженного совмещения $S$ является унитарным. Элемент $\sigma _{(uv)(vw)}$ из $S$ представляет собой комплексную амплитуду перехода от направленного края $(uv)$до края $(vw)$ что вообще зависит от $k$. Однако для большого класса условий совмещения S-матрица не зависит от $k$. Например, с условиями согласования Неймана

$A=\left({\begin{array}{ccccc}1&-1&0&0&\dots \\0&1&-1&0&\dots \\&&\ddots &\ddots &\\0&\dots &0&1&-1\\0&\dots &0&0&0\\\end{array}}\right),\quad B=\left({\begin{array}{cccc}0&0&\dots &0\\\vdots &\vdots &&\vdots \\0&0&\dots &0\\1&1&\dots &1\\\end{array}}\right).$

Подставив в уравнение $S$ производит $k$-независимые амплитуды перехода

$\sigma _{(uv)(vw)}={\frac {2}{d}}-\delta _{uw}.\,$

где $\delta _{uw}$ – дельта-функция Кронекера, которая равна единице, если $u=w$ и в противном случае ноль. По амплитудам перехода мы можем определить $2|E|\times 2|E|$ матрица

$U_{(uv)(lm)}(k)=\delta _{vl}\sigma _{(uv)(vm)}(k){\textrm {e}}^{ikL_{(uv)}}.\,$

$U$ называется матрицей рассеяния связи и можно рассматривать как оператор квантовой эволюции на графе. Этоунитарна и действует на вектор $2|E|$ коэффициенты плоской волны для график, где $c_{(uv)}$ коэффициент плоская волна, бегущая от $u$ к $v$. Этап ${\textrm {e}}^{ikL_{(uv)}}$ — фаза, приобретаемая плоской волной при распространении от вершины $u$ в вершину $v$.

Условие квантования: собственная функция на графике. может быть определен через связанный с ним $2|E|$ плосковолновые коэффициенты.Поскольку собственная функция стационарна при квантовой эволюции, квантование условие для графа можно записать с помощью оператора эволюции.

$|U(k)-I|=0.\,$

Собственные значения $k_{j}$ происходят при значениях $k$ где матрица $U(k)$ имеет собственное значение одно. Мы упорядочим спектр с $0\leqslant k_{0}\leqslant k_{1}\leqslant \dots$.

Первая формула следа для графа была выведена Ротом (1983).В 1997 году Коттос и Смилански использовали приведенное выше условие квантования, чтобы получитьследующую формулу следа для оператора Лапласа на графе, когдаамплитуды перехода не зависят от $k$.Формула следа связывает спектр с периодическими орбитами на графе.

$d(k):=\sum _{j=0}^{\infty }\delta (k-k_{j})={\frac {L}{\pi }}+{\frac {1}{\pi }}\sum _{p}{\frac {L_{p}}{r_{p}}}A_{p}\cos(kL_{p}).$

$d(k)$ называется плотностью состояний. Правая часть следа Формула состоит из двух членов: формулы Вейля срок ${\frac {L}{\pi }}$ - среднее расстояние между собственными значениями, а колеблющаяся часть представляет собой сумму по всем периодическим орбитам $p=(e_{1},e_{2},\dots ,e_{n})$ на графике. $L_{p}=\sum _{e\in p}L_{e}$ длина орбиты и $L=\sum _{e\in E}L_{e}$ являетсяобщая длина графа. Для орбиты, созданной повторением более короткая примитивная орбита, $r_{p}$ подсчитывает количество переделов. $A_{p}=\sigma _{e_{1}e_{2}}\sigma _{e_{2}e_{3}}\dots \sigma _{e_{n}e_{1}}$ является произведение амплитуд перехода в вершинах графа вокруг орбита.

Приложения

Молекула нафталина

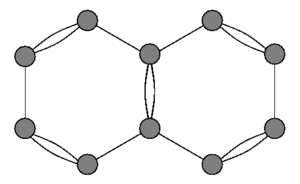
Квантовые графики впервые были использованы в 1930-х годах. моделировать спектр свободных электронов в органических молекулах, таких как Нафталин , см. рисунок. В первом приближении атомы считаются вершинами, а σ-электроны образуют связи, фиксирующие каркасв форме молекулы, на которой удерживаются свободные электроны.

Аналогичная проблема возникает при рассмотрении квантовых волноводов. Эти мезоскопические системы — системы, построенные с шириной в масштабенанометры. Квантовый волновод можно представить как расширенный граф. где краяпредставляют собой тонкие трубочки. Спектр оператора Лапласа в этой областисходится к спектру оператора Лапласа на графикепри определенных условиях. Понимание мезоскопических систем играет важную роль. важную роль в области нанотехнологий .

В 1997 году Коттос и Смилански предложили квантовые графы в качестве модели для изучения. квантовый хаос , квантовая механика систем, которые классически хаотичны. Классическое движение на графике можно определить как вероятностная цепь Маркова , где вероятность рассеяния с края $e$ к краю $f$ определяется абсолютным значением квадрат амплитуды квантового перехода, $|\sigma _{ef}|^{2}$. Почти для всех конечно связный квантовые графы, вероятностная динамика эргодическая и перемешивающая, другими словами, хаотичен.

В исследовании появляются квантовые графики, встроенные в два или три измерения.фотонных кристаллов . В двухмерном виде простая модель фотонный кристалл состоит из многоугольных ячеек плотного диэлектрика с узкие границы раздела ячеек, заполненные воздухом. Изучение диэлектрические моды, которые остаются в основном в диэлектрике, приводят к псевдодифференциальный оператор на графе, который следует за узкими интерфейсами.

Периодические квантовые графы, подобные решетке в ${\mathbb {R} }^{2}$ являются распространенными моделямибыли применены периодические системы и квантовые графы к изучению феномена локализации Андерсона там, где локализуются состояния возникают на краях спектральных полос при наличии беспорядка.

См. также

• Лестница Шильда , роман, посвященный вымышленной теории квантовых графов.
• Диаграмма Фейнмана