Батлер - уравнение Волмера
В электрохимии уравнение Батлера -Вольмера (названное в честь Джона Альфреда Валентина Батлера [ 1 ] и Max Volmer ), также известный как уравнение Erdey-Grúz -Volmer , является одной из самых фундаментальных отношений в электрохимической кинетике . Он описывает, как электрический ток через электрод зависит от разности напряжений между электродом и объемным электролитом для простой, немолекулярной окислительно -восстановительной реакции, учитывая, что как катодная , так и анодная реакция встречается на одном электроде : [ 2 ]
Уравнение дворецкого - Volmer
[ редактировать ]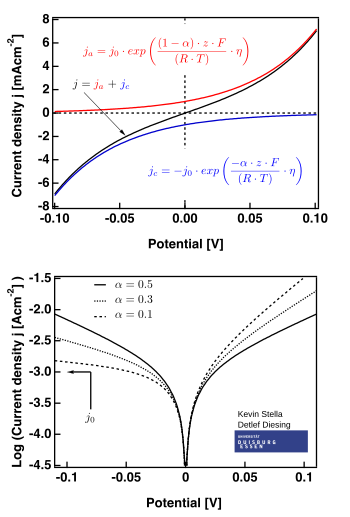
Уравнение дворецкого - Volmer:
или в более компактной форме:
где:
- : Плотность тока электрода , A/M 2 (определяется как j = i/s )
- : Обменная плотность тока , A/M 2
- : Потенциал электрода , V
- : равновесный потенциал, V
- : Абсолютная температура , k
- : Количество электронов, участвующих в реакции электрода
- : Faraday Constant
- : Universal Gas Constant
- : Так называемый коэффициент переноса катодного заряда , безразмерный
- : Так называемый коэффициент переноса анодного заряда, безразмерный
- : Активация чрезмерная (определяется как ).
На рисунке правой руки показаны графики действительными для .
Ограничивающие случаи
[ редактировать ]Есть два ограничивающих случая уравнения дворецкого -Volmer:
- область с низким уровнем чрезмерного возвышения (называемая «сопротивлением поляризации», т. Е., когда E ≈ E EQ ), где уравнение дворецкого -Volmer упрощает:
- ;
- Область высокой сверхпотенциальной, где уравнение Батлера -Volmer упрощает уравнение Тафеля . Когда , первый термин доминирует, и когда , второй термин доминирует.
- для катодной реакции, когда e << e eq , или
- для анодной реакции, когда E >> E EQ
где и являются постоянными (для данной реакции и температуры) и называются константами уравнения Тафеля. Теоретические значения констант уравнения Тафеля различны для катодных и анодных процессов. Тем не менее, склон Tafel можно определить как:
где Фарадаический ток, выраженный как , существование и Катодные и анодные частичные течения соответственно.
Расширенное уравнение Батлера -Volmer
[ редактировать ]Более общая форма уравнения Батлера-Фолмер, применимая к условиям, связанным с массой, может быть написана как: [ 3 ]
где:
- J - плотность тока, A/M 2 ,
- C O и C R относятся к концентрации видов, которые должны быть окислены и уменьшены соответственно,
- C (0, T)-это зависимая от времени концентрация на нуле на расстоянии от поверхности электрода.
Приведенная выше форма упрощает обычную (показанную в верхней части статьи), когда концентрация электроактивных видов на поверхности равна концентрации в объеме.
Существует две скорости, которые определяют отношение текущего напряжения для электрода. Во -первых, скорость химической реакции на электроде, которая потребляет реагенты и производит продукты. Это известно как скорость передачи заряда . Второе - это скорость, с которой предоставляются реагенты, и продукты удаляются из области электрода различными процессами, включая диффузию, миграцию и конвекцию. Последний известен как массового переноса скорость [ Примечание 1 ] Полем Эти две скорости определяют концентрации реагентов и продуктов на электроде, которые, в свою очередь, определяются ими. Самые медленные из этих скоростей будут определять общую скорость процесса.
Простое уравнение Батлера -Volmer предполагает, что концентрации на электроде практически равны концентрациям в объемном электролите, что позволяет выразить ток как функцию только потенциала. Другими словами, он предполагает, что скорость массопереноса намного выше, чем скорость реакции, и что в реакции преобладает более медленная скорость химической реакции. Несмотря на это ограничение, полезность уравнения Батлера -Фолмер в электрохимии широкая, и часто считается «центральной в феноменологической кинетике электродов». [ 4 ]
Расширенное уравнение Батлера -Volmer не делает это предположение, а скорее принимает концентрации на электроде, что дает, что дает взаимосвязь, в которой ток выражается как функция не только потенциала, но и заданных концентраций. Скорость массового переноса может быть относительно малой, но его единственное влияние на химическую реакцию заключается в измененных (данных) концентрациях. По сути, концентрации также являются функцией потенциала. Полная обработка, которая дает ток только в зависимости от потенциала, будет выражена расширенным уравнением дворецкого -Volmer, но потребует явного включения эффектов массопередачи, чтобы выразить концентрации как функции потенциала.
Вывод
[ редактировать ]Общее выражение
[ редактировать ]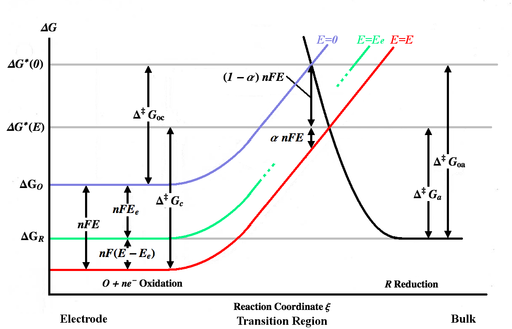
Следующее вывод расширенного уравнения Батлера -Фолмер адаптировано из урегулирования Барда и Фолкнера [ 3 ] и Ньюман и Томас-Алеа. [ 5 ] Для простой немолекулярной, одноэтапной реакции формы:
- O+ne − → r
вперед и назад Скорость реакции ( V F и V B ) и, по законам электролиза Фарадея , связанные с ними плотности электрического тока ( J ) могут быть написаны как:
где K F и K B являются константами скорости реакции , с единицами частоты (1/времени), а C O и C R являются поверхностными концентрациями (моль/область) окисленных и пониженных молекул, соответственно (написано как C O ( 0, T) и C R (0, T) в предыдущем разделе). Чистая скорость реакции v и плотности чистого тока J затем: [ Примечание 2 ]
На рисунке выше представлены различные кривые энергии Гиббса как функция координаты реакции ξ. Координата реакции является примерно мерой расстояния, при этом тело электрода находится слева, причем объемное решение находится справа. Кривая синей энергии показывает увеличение энергии Гиббса для окисленной молекулы, когда она движется ближе к поверхности электрода, когда потенциал не применяется. Кривая черной энергии показывает увеличение энергии Гиббса, поскольку уменьшенная молекула движется ближе к электроду. Две кривые энергии пересекаются на Полем Применение потенциала E к электроду переместит кривую энергии вниз. [ Примечание 3 ] (к красной кривой) с помощью NFE и точки пересечения перейдет к . и Энергии активации (энергетические барьеры) преодолеваются окисленными и восстановленными видами соответственно для общего E , в то время как и являются энергиями активации для e = 0 . [ Примечание 4 ]
Предположим, что константы скорости хорошо аппроксимируются уравнением Аррениуса ,
где A F и A B постоянными такими, что F C O являются = A B C R является «правильно ориентированной» или частотой столкновений, а экспоненциальный термин (фактор Больцмана) - это часть этих столкновений с достаточной энергией для преодоления барьер и реагировать.
Предполагая, что кривые энергии практически линейны в переходной области, они могут быть представлены там:
(Синяя кривая) (Красная кривая) (Черная кривая)
Коэффициент передачи заряда для этого простого случая эквивалентен фактору симметрии и может быть выражен в терминах наклонов кривых энергии:
Из этого следует:
Для краткости, определите:
Константы скорости теперь могут быть выражены как:
Где константы скорости с нулевым потенциалом:
Плотность тока J как функция применяемого потенциала E теперь может быть написана: [ 5 ] : § 8.3
Выражение с точки зрения равновесного потенциала
[ редактировать ]При определенном напряжении E E равновесие будет достигнуто, а скорости вперед и назад ( V F и V B ) будут равны. Это представлено зеленой кривой на приведенной выше рисунке. Константы скорости равновесия будут написаны как K Fe и K Be , а концентрации равновесия будут написаны C OE и C Re . Равновесные токи ( J CE и J AE ) будут равны и написаны как J O , который известен как плотность тока обмена .
Обратите внимание, что плотность чистого тока в равновесии будет равна нулю. Константы скорости равновесия тогда:
Решение вышеперечисленного для K FO и K BO с точки зрения равновесных концентраций C OE и C Re и плотности тока обмена J O , тока плотность J В зависимости от примененного потенциала E теперь может быть написана: [ 5 ] : § 8.3
Предполагая, что равновесие удерживается в объемном растворе, с концентрациями и , из этого следует, что и и вышеупомянутое выражение для плотности тока J является тогда уравнением дворецкого -Volmer. Обратите внимание, что Ee e также известен как η, активация чрезмерная .
Выражение с точки зрения формального потенциала
[ редактировать ]Для простой реакции изменение в энергии Гиббса: [ Примечание 5 ]
где OE равновесии и RE действиями являются в . Активность A связана с концентрациями c по A = γC, где γ является коэффициентом активности . Потенциал равновесия определяется уравнением Нернста :
где стандартный потенциал
Определение формального потенциала : [ 3 ] : § 2.1.6
Потенциал равновесия тогда:
Заменить этот потенциал равновесия в уравнение дворецкого -Volmer дает:
который также может быть написан в терминах стандартной постоянной скорости k а как: [ 3 ] : § 3.3.2
Стандартная константа скорости является важным дескриптором поведения электрода, независимо от концентраций. Это мера скорости, с которой система будет приближаться к равновесию. В пределе как Электрод становится идеальным поляризуемым электродом и будет вести себя электрически как открытая цепь (пренебрегая емкостью). Для почти идеальных электродов с маленькими k а Большие изменения в перепотенциале необходимы для создания значительного тока. В пределе как Электрод становится идеальным неполяризуемым электродом и будет вести себя как электрический короткий. Для почти идеальных электродов с большими k а Небольшие изменения в перепотенциале будут генерировать большие изменения в токе.
Смотрите также
[ редактировать ]- Усовершенствованная библиотека моделирования
- Уравнение Нернста
- Уравнение Голдмана
- Табличное уравнение
Примечания
[ редактировать ]- ^ Например, если скорость массо -переноса обусловлена только диффузией, существует максимальная скорость, с которой реагенты могут быть предоставлены для электрода, и, следовательно, максимальный возможный ток, известный как ограничивающий ток . Ограничивающий ток, когда процесс электрода сильно контролируется массовым переносом , значение плотности тока составляет:
- D EFF - это эффективный коэффициент диффузии (учитывая извинения , если таковые имеются);
- δ - толщина диффузионного слоя;
- в * является концентрацией электроактивных (ограничивающих) видов в основной части электролита.
- ^ Бард [ 3 ] Выбирает ток пропорциональным чистым прямом скорости, но выбирает потенциал E, который является тем, что электрод за исключением Electrolyte, который обладает смущающим (но не непоследовательным) эффектом дата положительного тока для отрицательного потенциала. Конвенция Ньюмана [ 5 ] в котором ток выбирается пропорционально чистой обратной скорости, используется здесь, чтобы соответствовать результатам вышеуказанных раздела.
- ^ Повышение потенциала ионов от нуля до E увеличит их к где это заряд на ионах (см. Электрохимический потенциал ). Увеличение потенциала электрода уменьшит потенциал ионов вблизи электрода по сравнению с электродом, уменьшая их .
- ^ На снижение кривой энергии (черная) может повлиять потенциал, но на выводы не влияют на это, если сумма окисления и уменьшения смещений кривой равна NFE [ 5 ]
- ^ Обратите внимание, что изменение энергии Гиббса также равно
Ссылки
[ редактировать ]- ^ Mayneord, WV (1979). « Джон Альфред Валентин Батлер , 14 февраля 1899 - 16 июля 1977 года». Биографические мемуары стипендиатов Королевского общества . 25 : 144–178. doi : 10.1098/rsbm.1979.0004 . PMID 11615791 . S2CID 1412298 .
- ^ Adler, SB (2016). «Глава 11: Источники потерь поляризации ячейки и электрода в SOFC». В Кендалле, Кевин; Кендалл, Микаэла (ред.). Высокотемпературные топливные элементы твердого оксида для 21-го века (2-е изд.). Академическая пресса. doi : 10.1016/c2011-0-09278-5 . ISBN 9780124104532 .
- ^ Подпрыгнуть до: а беременный в дюймовый и Бард, Аллен; Фолкнер, Ларри (2001). Электрохимические методы. Основы и приложения (2 -е изд.). Хобокен, Нью -Джерси: John Wiley & Sons, Inc. ISBN 978-0-471-04372-0 .
- ^ J. O'M. Bockris, Aknreddy и M. Gamboa-Adleco, «Современная электрохимия 2A. Основы электродики», второе издание, Kluwer Academic/Plenum Publishers, P.1083, 2000.
- ^ Подпрыгнуть до: а беременный в дюймовый и Ньюман, Джон; Томас-Алеа, Карен Э. (2004). Электрохимические системы (3 -е изд.). Хобокен, Нью -Джерси: John Wiley & Sons, Inc. ISBN 0-471-47756-7 .
Внешние ссылки
[ редактировать ] СМИ, связанные с уравнением Батлера-Вольмера в Wikimedia Commons
СМИ, связанные с уравнением Батлера-Вольмера в Wikimedia Commons
![{\ displayStyle j = j_ {0} \ cdot \ Left \ {\ exp \ Left [{\ frac {\ alpha _ {\ rm {a}} zf} {rt}} (e-e _ {\ rm {eq} }) \ right]-\ exp \ left [-{\ frac {\ alpha _ {\ rm {c}} zf} {rt}} (e-e _ {\ rm {eq}}) \ right] \ right \ }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f04ada917b1e46ab7d26da3300b2f080d9fd591a)
![{\ displayStyle j = j_ {0} \ cdot \ Left \ {\ exp \ Left [{\ frac {\ alpha _ {\ rm {a}} zf \ eta} {rt}} \ right]-\ exp \ left left [-{\ frac {\ alpha _ {\ rm {c}} zf \ eta} {rt}} \ right] \ right \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad7b1050149062da030fd2d606ff986928c8529)

























![{\ displayStyle j = j_ {0} \ left \ {{\ frac {c _ {\ rm {o}} (0, t)} {c _ {\ rm {o}}^{*}} \ exp \ [{\ frac {\ alpha _ {\ rm {a}} zf \ eta} {rt}} \ right]-{\ frac {c _ {\ rm {r}} (0, t)} {c _ {\ rm {r}}^{*}}} \ exp \ left [-{\ frac {\ alpha _ {\ rm {c}} zf \ eta} {rt}} \ right] \ right \}}}}}}}}}}}}}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba8cdc412ace94d2b8bd614a0c34bf817cca666)









![{\ displayStyle K_ {f} = a_ {f} \ exp [-\ delta ^{\ ddagge} g_ {c}/rt]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6665dbea2e1416b14eb890d7a632af7a69489c4c)
![{\ displayStyle K_ {b} = a_ {b} \ exp [-\ delta ^{\ ddagge} g_ {a}/rt]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b67f5c14cbc2f6dfa84ecae9c8c4cf62dfd96a9)





































