Перевернутый SU(5)

Модель «Перевернутого SU(5)» — это теория великого объединения (GUT), впервые предложенная Стивеном Барром в 1982 году. ^[1] и Дмитрия Нанопулоса и других в 1984 году. ^[2]^[3] Игнатиос Антониадис , Джон Эллис , Джон Хагелин и Дмитрий Нанопулос разработали суперсимметричную перевернутую SU(5), полученную из суперструны более глубокого уровня. ^[4]^[5]

Некоторые текущие попытки объяснить теоретические основы наблюдаемых масс нейтрино развиваются в контексте суперсимметричного перевернутого $SU(5)$ . ^[6]

Перевернутая $модель SU(5)$ не является полностью унифицированной моделью, поскольку $U(1) Y$ коэффициент группы датчиков Стандартной модели находится в пределах $коэффициента U(1)$ группы GUT. Добавление состояний ниже M в эту модель x при решении некоторых проблем пороговой коррекции в теории струн делает модель просто описательной, а не прогнозирующей. ^[7]

Модель

Перевернутая $модель SU (5)$ утверждает, что калибровочная группа :

(SU(5) \times U(1) χ)/ Z 5

Фермионы образуют три семейства, каждое из которых состоит из представлений

5 -3

для лептонного дублета L и верхних кварков

u с

;

101

для дублета кварков Q, нижнего кварка

d с

и правое нейтрино

N

;

15

для заряженных лептонов,

e с

.

Это отнесение включает три правых нейтрино, которые никогда не наблюдались, но часто постулируются для объяснения легкости наблюдаемых нейтрино и нейтринных осцилляций . Существует также $101$ и/или $10 -1,$ называемое полями Хиггса, которые приобретают VEV , что приводит к спонтанному нарушению симметрии.

(SU(5) \times U(1) χ)/ Z 5 \to (SU(3) \times SU(2) \times U(1) Y)/ Z 6

Представления $SU(5)$ преобразуются под действием этой подгруппы как приводимое представление следующим образом:

{\bar {5}}_{-3}\to ({\bar {3}},1)_{-{\frac {2}{3}}}\oplus (1,2)_{-{\frac {1}{2}}}

(в ^с и л)

10_{1}\to (3,2)_{\frac {1}{6}}\oplus ({\bar {3}},1)_{\frac {1}{3}}\oplus (1,1)_{0}

(д, д ^с и ν ^с)

1_{5}\to (1,1)_{1}

(и ^с)

24_{0}\to (8,1)_{0}\oplus (1,3)_{0}\oplus (1,1)_{0}\oplus (3,2)_{\frac {1}{6}}\oplus ({\bar {3}},2)_{-{\frac {1}{6}}}

.

Сравнение со стандартным SU(5)

Название «перевернутая» $SU(5)$ возникло в сравнении со «стандартной» $моделью SU(5)$ Джорджи–Глэшоу , в которой $u с$ и $д с$ кварку присвоены соответственно $10-$ и $5-$ представления. По сравнению со стандартным $SU(5)$ , перевернутый $SU(5)$ может осуществить спонтанное нарушение симметрии с использованием полей Хиггса размерности 10, в то время как стандартный $SU(5)$ обычно требует 24-мерного Хиггса. ^[8]

Соглашение о знаках для $U(1) χ$ варьируется от статьи/книги к статье.

Гиперзаряд Y/2 представляет собой линейную комбинацию (сумму) следующих факторов:

{\begin{pmatrix}{1 \over 15}&0&0&0&0\\0&{1 \over 15}&0&0&0\\0&0&{1 \over 15}&0&0\\0&0&0&-{1 \over 10}&0\\0&0&0&0&-{1 \over 10}\end{pmatrix}}\in {\text{SU}}(5),\qquad \chi /5.

Существуют также дополнительные поля $5 -2$ и $5 2,$ содержащие электрослабые дублеты Хиггса .

Называя представления , например, $5 -3$ и $24 0,$ это чисто физикское соглашение, а не математическое соглашение, где представления помечаются либо таблицами Юнга , либо диаграммами Дынкина с числами в их вершинах, и это стандарт, используемый GUT.теоретики.

Поскольку гомотопическая группа

\pi _{2}\left({\frac {[SU(5)\times U(1)_{\chi }]/\mathbf {Z} _{5}}{[SU(3)\times SU(2)\times U(1)_{Y}]/\mathbf {Z} _{6}}}\right)=0

эта модель не предсказывает монополи . См. монополь 'т Хоофта – Полякова .

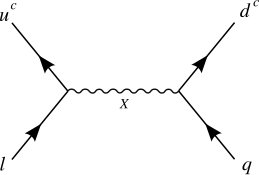
Минимальный суперсимметричный перевернутый SU (5)

Пространство-время

времени $. 3$ Расширение суперпространства N = 1 пространства- $+ 1$ Минковского

Пространственная симметрия

$N = 1$ SUSY в $пространстве-времени 3 + 1$ Минковского с R-симметрией

Группа калибровочной симметрии

$(SU(5) \times U(1) χ)/ Z 5$

Глобальная внутренняя симметрия

$Z 2$ (четность материи) $не связана с U(1) R$ никак для данной конкретной модели

Векторные суперполя

Связанные с $SU(5) \times U(1) χ.$ калибровочной симметрией

Хиральные суперполя

В качестве сложных представлений:

этикетка	описание	множественность	$SU(5) \times U(1) х$ реп.	$Z 2$ повторения	$У(1) Р$
$10 ч.$	Поле Хиггса GUT	$1$	$101$	+	$0$
$10 ч.$	Поле Хиггса GUT	$1$	$10 -1$	+	$0$
$Ч ты$	электрослабое поле Хиггса	$1$	$52$	+	$2$
$Х д$	электрослабое поле Хиггса	$1$	$5 -2$	+	$2$
$5$	поля материи	$3$	$5 -3$	-	$0$
$10$	поля материи	$3$	$101$	-	$0$
$1$	левый позитрон	$3$	$15$	-	$0$
$ж$	стерильное нейтрино (необязательно)	$3$	$10$	-	$2$
$С$	майка	$1$	$10$	+	$2$

Суперпотенциал

Типичный инвариантный перенормируемый суперпотенциал — это (комплексный) $SU(5) \times U(1) χ \times Z 2$ инвариантный кубический полином в суперполях, который имеет $R$ -заряд, равный 2. Это линейная комбинация следующих членов:

${\begin{matrix}S&S\\S10_{H}{\overline {10}}_{H}&S10_{H}^{\alpha \beta }{\overline {10}}_{H\alpha \beta }\\10_{H}10_{H}H_{d}&\epsilon _{\alpha \beta \gamma \delta \epsilon }10_{H}^{\alpha \beta }10_{H}^{\gamma \delta }H_{d}^{\epsilon }\\{\overline {10}}_{H}{\overline {10}}_{H}H_{u}&\epsilon ^{\alpha \beta \gamma \delta \epsilon }{\overline {10}}_{H\alpha \beta }{\overline {10}}_{H\gamma \delta }H_{u\epsilon }\\H_{d}1010&\epsilon _{\alpha \beta \gamma \delta \epsilon }H_{d}^{\alpha }10_{i}^{\beta \gamma }10_{j}^{\delta \epsilon }\\H_{d}{\bar {5}}1&H_{d}^{\alpha }{\bar {5}}_{i\alpha }1_{j}\\H_{u}10{\bar {5}}&H_{u\alpha }10_{i}^{\alpha \beta }{\bar {5}}_{j\beta }\\{\overline {10}}_{H}10\phi &{\overline {10}}_{H\alpha \beta }10_{i}^{\alpha \beta }\phi _{j}\\\end{matrix}}$

Во втором столбце каждый термин раскрывается в индексной записи (без учета надлежащего коэффициента нормализации). $i$ и $j$ — индексы поколений. Связь $H d 10 i 10 j$ имеет коэффициенты, симметричные по $i$ и $j$ .

В тех моделях, в которых отсутствуют необязательные $φ$ стерильные нейтрино, вместо этого мы добавляем неперенормируемые связи.

${\begin{matrix}({\overline {10}}_{H}10)({\overline {10}}_{H}10)&{\overline {10}}_{H\alpha \beta }10_{i}^{\alpha \beta }{\overline {10}}_{H\gamma \delta }10_{j}^{\gamma \delta }\\{\overline {10}}_{H}10{\overline {10}}_{H}10&{\overline {10}}_{H\alpha \beta }10_{i}^{\beta \gamma }{\overline {10}}_{H\gamma \delta }10_{j}^{\delta \alpha }\end{matrix}}$

Эти связи действительно нарушают R-симметрию.

См. также

Перевернутый ТАК(10)

Ссылки

^ Барр, С.М. (1982). «Новая картина нарушения симметрии SO (10) и распада протона». Буквы по физике Б. 112 (3): 219–222. дои : 10.1016/0370-2693(82)90966-2 .
^ Деренджер, Ж.-П.; Ким, Джин Э.; Нанопулос, Д.В. (1984). «Анти-Су(5)» . Буквы по физике Б. 139 (3): 170–176. дои : 10.1016/0370-2693(84)91238-3 .
^ Стенджер, Виктор Дж., Квантовые боги: творение, хаос и поиск космического сознания , Prometheus Books, 2009, 61. ISBN 978-1-59102-713-3
^ Антониадис, И.; Эллис, Джон; Хагелин, Дж. С.; Нанопулос, Д.В. (1988). «Построение модели GUT с фермионными четырехмерными струнами» . Буквы по физике Б. 205 (4): 459–465. дои : 10.1016/0370-2693(88)90978-1 . ОСТИ 1448495 .
^ Фридман, Д.Х. «Новая теория всего», Discover , 1991, 54–61.
^ Ризос, Дж.; Тамвакис, К. (2010). «Иерархические массы нейтрино и смешивание в перевернутом SU (5)». Буквы по физике Б. 685 (1): 67–71. arXiv : 0912.3997 . дои : 10.1016/j.physletb.2010.01.038 . ISSN 0370-2693 . S2CID 119210871 .
^ Баркоу, Тимоти и др. , Электрослабое нарушение симметрии и новая физика в ТэВном масштабе World Scientific, 1996, 194. ISBN 978-981-02-2631-2
^ Л.~Ф.~Ли,`` Групповая теория спонтанно нарушенной калибровочной симметрии , Физ. Ред. Д 9, 1723-1739 (1974) doi:10.1103/PhysRevD.9.1723

[1] Барр, С.М. (1982). «Новая картина нарушения симметрии SO (10) и распада протона». Буквы по физике Б. 112 (3): 219–222. дои : 10.1016/0370-2693(82)90966-2 .

[2] Деренджер, Ж.-П.; Ким, Джин Э.; Нанопулос, Д.В. (1984). «Анти-Су(5)» . Буквы по физике Б. 139 (3): 170–176. дои : 10.1016/0370-2693(84)91238-3 .

[3] Стенджер, Виктор Дж., Квантовые боги: творение, хаос и поиск космического сознания , Prometheus Books, 2009, 61. ISBN 978-1-59102-713-3

[4] Антониадис, И.; Эллис, Джон; Хагелин, Дж. С.; Нанопулос, Д.В. (1988). «Построение модели GUT с фермионными четырехмерными струнами» . Буквы по физике Б. 205 (4): 459–465. дои : 10.1016/0370-2693(88)90978-1 . ОСТИ 1448495 .

[5] Фридман, Д.Х. «Новая теория всего», Discover , 1991, 54–61.

[6] Ризос, Дж.; Тамвакис, К. (2010). «Иерархические массы нейтрино и смешивание в перевернутом SU (5)». Буквы по физике Б. 685 (1): 67–71. arXiv : 0912.3997 . дои : 10.1016/j.physletb.2010.01.038 . ISSN 0370-2693 . S2CID 119210871 .

[7] Баркоу, Тимоти и др. , Электрослабое нарушение симметрии и новая физика в ТэВном масштабе World Scientific, 1996, 194. ISBN 978-981-02-2631-2

[8] Л.~Ф.~Ли,`` Групповая теория спонтанно нарушенной калибровочной симметрии , Физ. Ред. Д 9, 1723-1739 (1974) doi:10.1103/PhysRevD.9.1723

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]