Круглое сечение

Не путать с круговым сектором .

трехосный эллипсоид круглого сечения

В геометрии круглое сечение — это круг на квадратичной поверхности (например, эллипсоид или гиперболоид ). Это особое плоское сечение квадрики, так как эта окружность является пересечением с квадрикой плоскости, содержащей окружность.

Любое плоское сечение сферы является круговым, если оно содержит хотя бы две точки. Любая квадрика вращения содержит окружности как сечения с плоскостями, ортогональными ее оси; он не содержит никаких других кругов, если это не сфера. Более скрыты окружности на других квадриках, например трехосных эллипсоидах, эллиптических цилиндрах и т. д. Тем не менее верно и то, что:

• Любая квадрика, содержащая эллипсы, содержит и круги.

Эквивалентно, все квадратические поверхности содержат круги, за исключением параболических и гиперболических цилиндров и гиперболических параболоидов .

Если квадрика содержит окружность, то каждое пересечение квадрики плоскостью, параллельной этой окружности, также является окружностью, если оно содержит хотя бы две точки. За исключением сфер, все окружности, содержащиеся в квадрике, если таковые имеются, параллельны одной из двух фиксированных плоскостей (которые равны в случае квадрики вращения).

Круглые сечения используются в кристаллографии .

Использование проективной геометрии

Круговые сечения квадрики можно вычислить из неявного уравнения квадрики, как это делается в следующих разделах. Их также можно охарактеризовать и изучить с помощью синтетической проективной геометрии .

Пусть C пересечение квадрики Q и плоскости P. — В этом разделе Q и C — поверхности в трехмерном евклидовом пространстве , которые расширяются до проективного пространства над комплексными числами . При этих гипотезах кривая C является окружностью тогда и только тогда, когда ее пересечение с бесконечной плоскостью входит в омбилику (бесконечную кривую уравнения $x^{2}+y^{2}+z^{2}=0$).

Первый случай, который следует рассмотреть, - это когда пересечение Q с плоскостью на бесконечности состоит из одной или двух действительных линий, то есть когда Q является либо гиперболическим параболоидом , либо параболическим цилиндром , либо гиперболическим цилиндром . В этом случае точки на бесконечности C являются вещественными (пересечение вещественной плоскости с вещественными прямыми). Таким образом, плоские сечения Q не могут быть ни кругами (ни эллипсами ).

Если Q — сфера , то ее пересечение с плоскостью на бесконечности — это омбилика, а все сечения плоскости — круги.

Если Q — поверхность вращения , то ее пересечение с омбиликой состоит из пары комплексно-сопряженных точек (которые являются двойными точками ). Реальная плоскость содержит эти две точки тогда и только тогда, когда она перпендикулярна оси вращения. Таким образом, круговые сечения — это плоские сечения плоскостью, перпендикулярной оси, имеющие не менее двух действительных точек.

В остальных случаях пересечение Q с омбиликой состоит из двух разных пар комплексно-сопряженных точек. Поскольку C — кривая второй степени, ее пересечение с бесконечно удаленной плоскостью состоит из двух точек, возможно, равных. Таким образом, кривая C является окружностью, если эти две точки являются одной из этих двух пар комплексно-сопряженных точек на омбилике. Каждая из этих пар определяет действительную линию (проходящую через точки), которая является пересечением P с плоскостью, находящейся на бесконечности. Таким образом, существует круговое сечение тогда и только тогда, когда C имеет по крайней мере две действительные точки, а P содержит одну из этих прямых на бесконечности (то есть, если P параллельна одному из двух направлений, определяемых этими линиями на бесконечности).

Определение круговых сечений квадрики

Чтобы найти плоскости, содержащие круговые сечения данной квадрики, используются следующие утверждения:

(S:) Если точки пересечения квадрики со сферой содержатся в паре плоскостей, то кривая пересечения состоит из двух окружностей.

(П:) Если пересечением плоскости и квадрики является окружность, то любая параллельная плоскость, содержащая хотя бы две точки квадрики, пересекает квадрику и по окружности.

Следовательно, стратегия обнаружения круглых участков следующая:

1) Найдите сферу , пересекающую квадрику в паре плоскостей и

2) Плоскости , параллельные обнаруженным, доставляют оставшиеся круговые сечения.

Трехосный эллипсоид

трехосный эллипсоид с круглыми сечениями (синий и зеленый) и вспомогательной сферой (красный), пересекающей квадрику в синих кружках

Эллипсоид, пересекаемый сферами: $c<{\color {seagreen}r_{1}}<{\color {blue}b}<{\color {purple}r_{2}}<a$

Для эллипсоида с уравнением

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

и полуоси $a>b>c>0$ используется вспомогательная сфера с уравнением

$x^{2}+y^{2}+z^{2}=r^{2}\ .$

Радиус сферы должен быть выбран таким, чтобы пересечение с эллипсоидом находилось в двух плоскостях, проходящих через начало координат.Умножение уравнения эллипсоида на $r^{2}$ и вычитание уравнения сферы дает:

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}+\left({\frac {r^{2}}{c^{2}}}-1\right)\;z^{2}=0\ .$

Это уравнение описывает пару плоскостей, если один из трех коэффициентов равен нулю. В случае $\ r=a\$ или $\ r=c\$ уравнение выполняется только по оси X или оси Z. Только в случае $\ r=b\$ получаем пару плоскостей с уравнением

• $\left({\frac {b^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {b^{2}}{c^{2}}}-1\right)\;z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\tfrac {c}{a}}{\sqrt {\tfrac {a^{2}-b^{2}}{b^{2}-c^{2}}}}\;x\ ,$

потому что только в этом случае остальные коэффициенты имеют разные знаки (из-за: $a>b>c$).

Диаграмма дает представление о более распространенных пересечениях сферы и эллипсоида и подчеркивает исключительный круглый случай (синий).

Если значения полуосей приближаются, то приближаются и два пучка плоскостей (и окружностей). Для $a=b$ все плоскости ортогональны оси z (оси вращения).

Доказательство собственности (P)

Поворот эллипсоида вокруг оси Y так, чтобы один из двух кругов (синий) лежал в плоскости XY, приводит к новому уравнению эллипсоида:

$Ax^{2}+By^{2}+Cz^{2}+D{\color {red}xz}=E$

Для $z=0$ каждый получает $Ax^{2}+By^{2}=E$, которое должно быть уравнением окружности. Это верно только в том случае, если $A=B\neq 0,\ E>0$. Пересечение эллипсоида плоскостью с уравнением $z=z_{0}$, (параллельно плоскости xy) имеет уравнение

$A(x^{2}+y^{2})+Dz_{0}x=E-Cz_{0}^{2}$.

Это уравнение описывает круг , точку или пустое множество. Центр и радиус круга можно найти, дополняя квадрат .

Эллиптический однолистный гиперболоид

однолистный гиперболоид

Для гиперболоида однополостного с уравнением

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,c>0$

аналогично получается для пересечения со сферой $\ x^{2}+y^{2}+z^{2}=r^{2}\$ уравнение

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}-\left({\frac {r^{2}}{c^{2}}}+1\right)\;z^{2}=0\ .$

Только для $\ r=a\$ получается пара самолетов:

$\left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-\left({\frac {a^{2}}{c^{2}}}+1\right)\;z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2}}{a^{2}+c^{2}}}}\;y\ ,\$

Эллиптический цилиндр

эллиптический цилиндр

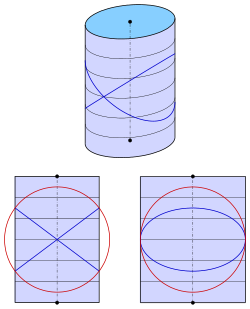
Для эллиптического цилиндра с уравнением

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\ ,\quad a>b\ ,$

получается уравнение

$\left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}-z^{2}=0\ .$

Только для $\ r=a\$ получается пара самолетов:

$\left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\frac {\sqrt {a^{2}-b^{2}}}{b}}\;y\ .\$

Эллиптический параболоид

эллиптический параболоид

Для эллиптического параболоида с уравнением

$ax^{2}+by^{2}-z=0\ ,\quad a{\color {red}{<}}b\ ,$

выбирается сфера, содержащая вершину (начало координат) и с центром на оси (ось z):

$x^{2}+y^{2}+(z-r)^{2}=r^{2}\quad \leftrightarrow \quad x^{2}+y^{2}+z^{2}-2rz=0\ .$

После исключения линейных частей получаем уравнение

$(2ra-1)\;x^{2}+(2rb-1)\;y^{2}-z^{2}=0\ .$

Только для $r={\tfrac {1}{2a}}$ получается пара самолетов:

$\left({\frac {b}{a}}-1\right)\;y^{2}-z^{2}=0\quad \leftrightarrow \quad z=\pm {\sqrt {\frac {b-a}{a}}}\;y\ .\$

Эллиптический гиперболоид из двух листов

эллиптический гиперболоид из двух листов

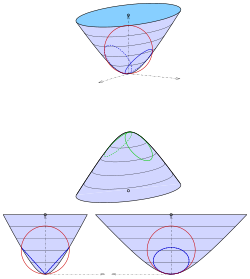
Гиперболоид уравнением двух листов с

$-{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,\ c>0\ ,$

сначала смещается так, что одна вершина является началом координат (см. диаграмму):

$-{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {(z+c)^{2}}{c^{2}}}=1\quad \leftrightarrow \quad \ -{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}+{\frac {2z}{c}}=0\ .$

Аналогично случаю параболоида выбирается сфера, содержащая начало координат с центром на оси z:

$x^{2}+y^{2}+(z-r)^{2}=r^{2}\quad \leftrightarrow \quad x^{2}+y^{2}+z^{2}-2zr=0\ .$

После исключения линейных частей получаем уравнение

$\left(-{\frac {r}{a^{2}}}+{\frac {1}{c}}\right)\;x^{2}+\left(-{\frac {r}{b^{2}}}+{\frac {1}{c}}\right)\;y^{2}+\left({\frac {r}{c^{2}}}+{\frac {1}{c}}\right)z^{2}=0\ .$

Только для $r={\tfrac {a^{2}}{c}}$ получается пара самолетов:

$\left(-{\frac {a^{2}}{b^{2}c}}+{\frac {1}{c}}\right)\;y^{2}+\left({\frac {a^{2}}{c^{3}}}+{\frac {1}{c}}\right)\;z^{2}=0\ \quad \leftrightarrow \quad z=\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2}}{a^{2}+c^{2}}}}\;y\ .$

Эллиптический конус

эллиптический конус

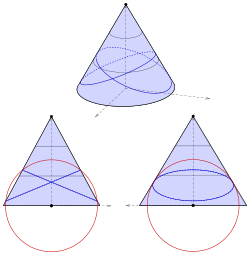
Эллиптический конус с уравнением

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z^{2}=0\ ,\quad a>b\ ,$

сдвинута так, что вершина не является началом координат (см. диаграмму):

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-(z-1)^{2}=0\quad \leftrightarrow \quad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z^{2}+2z=1.$

Теперь подойдет сфера с центром в начале координат:

$x^{2}+y^{2}+z^{2}=r^{2}\ .$

Устранение $x^{2}$ дает:

$\left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-(1+a^{2})\;z^{2}+2a^{2}z=a^{2}-r^{2}\ .$

В этом случае заполнение квадрата дает:

${\frac {a^{2}-b^{2}}{b^{2}}}\;y^{2}-(1+a^{2})\left(z-{\frac {a^{2}}{1+a^{2}}}\right)^{2}=a^{2}-{\frac {a^{4}}{1+a^{2}}}-r^{2}\ .$

Чтобы получить уравнение пары плоскостей, правая часть уравнения должна быть равна нулю, что справедливо для $r={\tfrac {a}{\sqrt {1+a^{2}}}}\ .$Решение для z дает:

$z={\frac {a^{2}}{1+a^{2}}}\pm {\frac {1}{b}}{\sqrt {\frac {a^{2}-b^{2}}{1+a^{2}}}}\;y\ .$

Ссылки

• Х. Ф. Бейкер: Принципы геометрии, Том 3 , Издательство Кембриджского университета, 2010 г., ISBN   978-1-108-01779-4 .
• ДМИ Соммервилль: Аналитическая геометрия трех измерений , Издательство Кембриджского университета, 1959, ISBN   978-1-316-60190-7 , с. 204.
• К. П. Гротемейер: Аналитическая геометрия. Гёшен-Верлаг, 1962, с. 143.
• Х. Шейд, В. Шварц: Элементы линейной алгебры и анализа. Спектр, Гейдельберг, 2009 г., ISBN   978-3-8274-1971-2 , с. 132.

Внешние ссылки

• Х. Винер, П. Тройтляйн: Модели трехосного эллипсоида и эллиптического параболоида с использованием круглых сечений (см. стр. 15) [1] (PDF).