Отношение площади поверхности к объему
Отношение площади поверхности к объему или отношение поверхности к объему (обозначаемое как SA:V , SA/V или sa/vol ) — это соотношение между площадью поверхности и объемом объекта или набора объектов.
SA:V — важная концепция в науке и технике. Он используется для объяснения связи между структурой и функцией в процессах, происходящих через поверхность и объем. Хорошими примерами таких процессов являются процессы, управляемые уравнением теплопроводности : [1] то есть диффузия и передача тепла посредством теплопроводности . [2] SA:V используется для объяснения диффузии небольших молекул, таких как кислород и углекислый газ, между воздухом, кровью и клетками. [3] потеря воды животными, [4] бактериальный морфогенез, [5] организма терморегуляция , [6] проектирование искусственной костной ткани, [7] искусственные легкие [8] и многие другие биологические и биотехнологические структуры. Дополнительные примеры см. в разделе Стекольщик. [9]
Связь между SA:V и скоростью диффузии или теплопроводности объясняется с точки зрения потока и поверхности, при этом основное внимание уделяется поверхности тела как месту, где происходит диффузия или теплопроводность, т.е. чем больше SA:V, тем больше SA:V. большая площадь поверхности на единицу объема, через которую может диффундировать материал, следовательно, диффузия или теплопроводность будут происходить быстрее. Аналогичное объяснение встречается в литературе: «Малый размер подразумевает большое соотношение площади поверхности к объему, что помогает максимизировать поглощение питательных веществ через плазматическую мембрану». [10] и в других местах. [9] [11] [12]
Для данного объема объект с наименьшей площадью поверхности (и, следовательно, с наименьшим SA:V) представляет собой шар , что является следствием изопериметрического неравенства в трех измерениях . Напротив, объекты с остроугольными шипами будут иметь очень большую площадь поверхности для данного объема.
Для твердых сфер
[ редактировать ]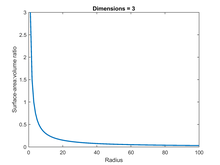
или Твердая сфера шар — это трёхмерный объект, представляющий собой твёрдую фигуру, ограниченную сферой . (В геометрии термин «сфера» сфере не хватает объема правильно относится только к поверхности, поэтому в этом контексте .)
Для обычного трехмерного шара SA:V можно рассчитать, используя стандартные уравнения для поверхности и объема, которые имеют вид соответственно: и . Таким образом , для единичного случая, когда r = 1, SA:V равно 3. В общем случае SA:V равно 3/ r в обратной зависимости от радиуса - если радиус удваивается, SA:V уменьшается вдвое ( см. рисунок).
Для n -мерных шаров
[ редактировать ]Шары существуют в любом измерении и обычно называются n -шарами или гипершарами , где n — количество измерений. Те же рассуждения можно обобщить на n-шары, используя общие уравнения для объема и площади поверхности, а именно:
Таким образом, соотношение равно . Таким образом, одна и та же линейная зависимость между площадью и объемом сохраняется для любого количества измерений (см. рисунок): удвоение радиуса всегда уменьшает соотношение вдвое.
Размер и единицы измерения
[ редактировать ]Отношение площади поверхности к объему имеет физический размер, обратный длине (L −1 ) и поэтому выражается в единицах обратного метра (м -1 ) или его с префиксом кратные и дольные единицы . Например, куб со стороной 1 см будет иметь площадь поверхности 6 см. 2 и объём 1 см. 3 . Таким образом, отношение поверхности к объему для этого куба равно
- .
Для данной формы SA:V обратно пропорционально размеру. Куб со стороной 2 см имеет отношение 3 см. −1 , что вдвое меньше куба со стороной 1 см. И наоборот, сохранение SA:V по мере увеличения размера требует изменения формы до менее компактной .
Приложения
[ редактировать ]Физическая химия
[ редактировать ]Материалы с высоким соотношением площади поверхности к объему (например, очень маленького диаметра, очень пористые или по другим причинам некомпактные ) реагируют гораздо быстрее, чем монолитные материалы, поскольку для реакции доступна большая поверхность. Примером может служить зерновая пыль: хотя зерно обычно не является горючим, зерновая пыль взрывоопасна . Мелко помолотая соль растворяется гораздо быстрее, чем крупная.
Высокое соотношение площади поверхности к объему обеспечивает сильную «движущую силу» для ускорения термодинамических процессов, которые минимизируют свободную энергию .
Биология
[ редактировать ]
Соотношение площади поверхности и объема клеток и организмов оказывает огромное влияние на их биологию , включая физиологию и поведение . Например, многие водные микроорганизмы увеличили площадь поверхности, чтобы увеличить сопротивление воде. Это снижает скорость их погружения и позволяет им оставаться у поверхности с меньшими затратами энергии. [ нужна ссылка ]
Увеличение соотношения площади поверхности к объему также означает повышенное воздействие окружающей среды. Мелкоразветвленные придатки фильтраторов, таких как криль, обеспечивают большую площадь поверхности для просеивания воды для получения пищи. [13]
Отдельные органы, такие как легкие, имеют многочисленные внутренние разветвления, которые увеличивают площадь поверхности; в случае легких большая поверхность поддерживает газообмен, доставляя кислород в кровь и выделяя углекислый газ из крови. [14] [15] Точно так же тонкая кишка имеет мелкоморщинистую внутреннюю поверхность, что позволяет организму эффективно усваивать питательные вещества. [16]
Клетки могут достигать высокого соотношения площади поверхности к объему со сложной извитой поверхностью, как у микроворсинок, выстилающих тонкую кишку . [17]
Увеличение площади поверхности также может привести к биологическим проблемам. Увеличение контакта с окружающей средой через поверхность клетки или органа (по отношению к ее объему) увеличивает потерю воды и растворенных веществ. Высокое соотношение площади поверхности к объему также создает проблемы контроля температуры в неблагоприятных условиях. [ нужна ссылка ]
Соотношение поверхности и объема организмов разных размеров также приводит к некоторым биологическим правилам, таким как правило Аллена , правило Бергмана. [18] [19] [20] и гигантотермия . [21]
Распространение огня
[ редактировать ]В контексте лесных пожаров важным показателем является отношение площади поверхности твердого топлива к его объему. Характер распространения огня часто коррелирует с соотношением площади поверхности к объему топлива (например, листьев и ветвей). Чем выше его значение, тем быстрее частица реагирует на изменения условий окружающей среды, например, температуры или влажности. Более высокие значения также коррелируют с более коротким временем воспламенения топлива и, следовательно, с более высокой скоростью распространения огня.
Планетарное охлаждение
[ редактировать ]Тело из ледяного или каменистого материала в космическом пространстве может, если оно способно накапливать и сохранять достаточно тепла, иметь дифференцированную внутреннюю часть и изменять свою поверхность в результате вулканической или тектонической активности. Продолжительность времени, в течение которого планетарное тело может поддерживать активность, изменяющую поверхность, зависит от того, насколько хорошо оно сохраняет тепло, и это определяется соотношением площади его поверхности к объему. Для Весты (r=263 км) это соотношение настолько велико, что астрономы были удивлены, обнаружив, что она действительно дифференцирована и имеет кратковременную вулканическую активность. Луна ; , Меркурий и Марс имеют радиусы в несколько тысяч километров все три достаточно хорошо сохраняли тепло, чтобы их можно было тщательно дифференцировать, хотя примерно через миллиард лет они стали слишком холодными, чтобы проявлять что-либо большее, чем очень локализованную и нечастую вулканическую активность. Однако по состоянию на апрель 2019 года НАСА объявило об обнаружении «марсотрясения», измеренного 6 апреля 2019 года спускаемым аппаратом НАСА InSight. [22] Венера и Земля (r>6000 км) имеют достаточно низкое соотношение площади поверхности к объему (примерно вдвое меньше, чем у Марса, и намного ниже, чем у всех других известных каменистых тел), поэтому их теплопотери минимальны. [23]
Математические примеры
[ редактировать ]
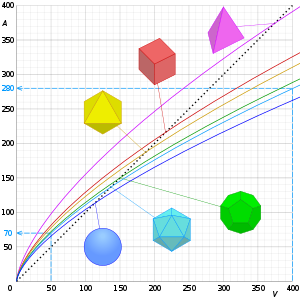
| Форма | Изображение | Характеристика длина |
SA/V ratio | SA/V ratio for единица объема |
|---|---|---|---|---|
| Тетраэдр | 
|
край | 7.21 | |
| Куб | 
|
край | 6 | |
| Октаэдр | 
|
край | 5.72 | |
| Додекаэдр | 
|
край | 5.31 | |
| Капсула | 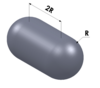
|
радиус (R) | 5.251 | |
| Икосаэдр | 
|
край | 5.148 | |
| Сфера | 
|
радиус | 4.83598 |
| Сторона куб |
Сторона 2 | Площадь одно лицо |
6 × сторона 2 | Площадь весь куб (6 лиц) |
Сторона 3 | Объем | Соотношение площадь поверхности объем |
|---|---|---|---|---|---|---|---|
| 2 | 2×2 | 4 | 6×2×2 | 24 | 2×2×2 | 8 | 3:1 |
| 4 | 4×4 | 16 | 6×4×4 | 96 | 4×4×4 | 64 | 3:2 |
| 6 | 6×6 | 36 | 6×6×6 | 216 | 6×6×6 | 216 | 3:3 |
| 8 | 8×8 | 64 | 6×8×8 | 384 | 8×8×8 | 512 | 3:4 |
| 12 | 12×12 | 144 | 6×12×12 | 864 | 12×12×12 | 1,728 | 3:6 |
| 20 | 20×20 | 400 | 6×20×20 | 2,400 | 20×20×20 | 8,000 | 3:10 |
| 50 | 50×50 | 2,500 | 6×50×50 | 15,000 | 50×50×50 | 125,000 | 3:25 |
| 1,000 | 1,000×1,000 | 1,000,000 | 6×1,000×1,000 | 6,000,000 | 1,000×1,000×1,000 | 1,000,000,000 | 3:500 |
См. также
[ редактировать ]Ссылки
[ редактировать ]- Шмидт-Нильсен, Кнут (1984). Масштабирование: почему размер животного так важен? . Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-26657-4 . ОСЛК 10697247 .
- Фогель, Стивен (1988). Устройства жизни: физический мир животных и растений . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 978-0-691-08504-3 . OCLC 18070616 .
- Специфический
- ^ Планиншич, Горазд; Фоллмер, Майкл (20 февраля 2008 г.). «Отношение поверхности к объему в теплофизике: от физики сырных кубиков к метаболизму животных» . Европейский журнал физики . 29 (2): 369–384. Бибкод : 2008EJPh...29..369P . дои : 10.1088/0143-0807/29/2/017 . S2CID 55488270 . Проверено 9 июля 2021 г.
- ^ Планиншич, Горазд (2008). «Отношение поверхности к объему в теплофизике: от физики сырных кубиков к метаболизму животных» . Европейский журнал физики. Европейское физическое общество. Узнайте больше . 29 (2): 369–384. Бибкод : 2008EJPh...29..369P . дои : 10.1088/0143-0807/29/2/017 . S2CID 55488270 .
- ^ Уильямс, Питер; Уорик, Роджер; Дайсон, Мэри; Баннистер, Лоуренс Х. (2005). Анатомия Грея (39-е изд.). Черчилль Ливингстон. стр. 1278–1282.
- ^ Джереми М., Ховард; Ханна-Бет, Гриффис; Вестендорф, Рэйчел; Уильямс, Джейсон Б. (2019). «Влияние размера и абиотических факторов на потерю воды через кожу» . Достижения в области физиологического образования . 44 (3): 387–393. дои : 10.1152/advan.00152.2019 . ПМИД 32628526 .
- ^ Харрис, Ли К.; Териот, Джули А. (2018). «Отношение площади поверхности к объему: естественная переменная бактериального морфогенеза» . Тенденции в микробиологии . 26 (10): 815–832. дои : 10.1016/j.tim.2018.04.008 . ПМК 6150810 . ПМИД 29843923 .
- ^ Лоу, Гидеон Н. (1993). Физиологическая экология животных . Группа пабов Лонгман.
- ^ Нгуен, Тхань Дань; Олуфеми Э., Кадри; Василиос И., Сикавицас; Воронов, Роман С. (2019). «Скаффолды с высоким соотношением площади поверхности к объему, культивируемые в условиях перфузии с быстрым потоком, приводят к оптимальной доставке O2 к клеткам в искусственных костных тканях» . Прикладные науки . 9 (11): 2381. дои : 10.3390/app9112381 .
- ^ Дж. К., Ли; ХХ, Кунг; Л.Ф., Мокрос (2008). «Микроканальные технологии для искусственных легких: (1) Теория» . Журнал АСАИО . 54 (4): 372–382. дои : 10.1097/MAT.0b013e31817ed9e1 . ПМИД 18645354 . S2CID 19505655 .
- ^ Jump up to: а б Стекольщик, Дуглас С. (2010). «Объединяющее объяснение разнообразия метаболических процессов у животных и растений» . Биологические обзоры . 85 (1): 111–138. дои : 10.1111/j.1469-185X.2009.00095.x . ПМИД 19895606 . S2CID 28572410 .
- ^ Альбертс, Брюс (2002). «Разнообразие геномов и древо жизни». Молекулярная биология клетки, 4-е издание . Нью-Йорк: Garland Science. ISBN 0-8153-3218-1 . ISBN 0-8153-4072-9 .
- ^ Адам, Джон (01 января 2020 г.). «Каков ваш индекс сферичности? Рационализация площади поверхности и объема» . Учитель математики в Вирджинии . 46 (2).
- ^ Оки, Джордан Г. (март 2013 г.). «Общие модели спектров стратегий масштабирования площади поверхности клеток и организмов: фрактальность, геометрическое несходство и интернализация» . Американский натуралист . 181 (3): 421–439. дои : 10.1086/669150 . ISSN 1537-5323 . ПМИД 23448890 . S2CID 23434720 .
- ^ Килс, У.: Плавание и кормление антарктического криля, Euphausia superba — выдающаяся энергетика и динамика — некоторые уникальные морфологические детали . In Berichte zur Polarforschung , Институт полярных и морских исследований Альфреда Вегенера , специальный выпуск 4 (1983): «О биологии криля Euphausia superba », Труды семинара и отчет группы экологии криля, редактор С.Б. Шнак, 130-155 и изображение титульного листа.
- ^ Тортора, Джерард Дж.; Анагностакос, Николас П. (1987). Основы анатомии и физиологии (Пятое изд.). Нью-Йорк: Harper & Row, Издательство. стр. 100-1 556–582 . ISBN 978-0-06-350729-6 .
- ^ Уильямс, Питер Л.; Уорик, Роджер; Дайсон, Мэри; Баннистер, Лоуренс Х. (1989). Анатомия Грея (тридцать седьмое изд.). Эдинбург: Черчилль Ливингстон. стр. 1278–1282. ISBN 0443-041776 .
- ^ Ромер, Альфред Шервуд; Парсонс, Томас С. (1977). Тело позвоночного . Филадельфия, Пенсильвания: Холт-Сондерс Интернэшнл. стр. 349–353. ISBN 978-0-03-910284-5 .
- ^ Краузе Дж. Уильям (июль 2005 г.). Основная гистология человека Краузе для студентов-медиков . Универсал-Издательство. стр. 37–. ISBN 978-1-58112-468-2 . Проверено 25 ноября 2010 г.
- ^ Мейри, С.; Даян, Т. (20 марта 2003 г.). «О справедливости правила Бергмана». Журнал биогеографии . 30 (3): 331–351. Бибкод : 2003JBiog..30..331M . дои : 10.1046/j.1365-2699.2003.00837.x . S2CID 11954818 .
- ^ Эштон, Кайл Г.; Трейси, Марк С.; Кейруш, Алан де (октябрь 2000 г.). «Действительно ли правило Бергмана для млекопитающих?». Американский натуралист . 156 (4): 390–415. дои : 10.1086/303400 . JSTOR 10.1086/303400 . ПМИД 29592141 . S2CID 205983729 .
- ^ Миллиен, Вирджиния; Лайонс, С. Кэтлин; Олсон, Линк; и др. (23 мая 2006 г.). «Экотипические вариации в контексте глобального изменения климата: пересмотр правил». Экологические письма . 9 (7): 853–869. Бибкод : 2006EcolL...9..853M . дои : 10.1111/j.1461-0248.2006.00928.x . ПМИД 16796576 .
- ^ Фитцпатрик, Кэти (2005). «Гигантотермия» . Дэвидсон Колледж . Архивировано из оригинала 30 июня 2012 г. Проверено 21 декабря 2011 г.
- ^ «Марсотрясение! Посадочный модуль НАСА InSight почувствовал первое сотрясение Красной планеты» . Space.com . 23 апреля 2019 г.
- ^ «Архивная копия» (PDF) . Архивировано из оригинала (PDF) 13 июня 2018 г. Проверено 22 августа 2018 г.
{{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )
Внешние ссылки
[ редактировать ]- Размеры организмов: площадь поверхности: соотношение объемов. Архивировано 14 августа 2017 г. на Wayback Machine.
- Национальная координационная группа по лесным пожарам: соотношение площади поверхности к объему
- Предыдущая ссылка не работает, ссылки находятся в этом документе, PDF.
Дальнейшее чтение
[ редактировать ]- О правильном размере, JBS Haldane. Архивировано 22 августа 2011 г. в Wayback Machine.













