Гномон (фигура)

В геометрии гномон аналогичного — плоская фигура, образованная удалением параллелограмма из угла большего параллелограмма; или, в более общем смысле, фигура, которая, добавленная к данной фигуре, образует большую фигуру той же формы. [1]
Построение фигурных чисел
[ редактировать ]Фигурные числа были предметом озабоченности пифагорейской математики , и Пифагору приписывают идею, что эти числа производятся из гномона или базовой единицы. Гномон — это деталь, которую нужно прибавить к фигурному числу, чтобы превратить его в следующее большее число. [2]
Например, гномоном квадратного числа является нечетное число общего вида 2 n + 1, n = 1, 2, 3,... . Квадрат размера 8, составленный из гномонов, выглядит так:
Для преобразования n-квадрата (квадрата размера n ) в ( n + 1)-квадрат необходимо присоединить 2 n + 1 элементов: по одному к концу каждой строки ( n элементов), по одному к концу каждой столбец ( n элементов) и один в углу. Например, при преобразовании квадрата 7 в квадрат 8 мы добавляем 15 элементов; эти присоединения обозначены восьмерками на рисунке выше. Этот гномонический метод также обеспечивает доказательство того, что сумма первых n нечетных чисел равна n 2 ; на рисунке показано 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64 = 8. 2 .

Применение той же техники к таблице умножения дает теорему Никомаха , доказывающую, что каждый квадрат треугольного числа представляет собой сумму кубов. [3]
Равнобедренные треугольники
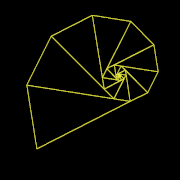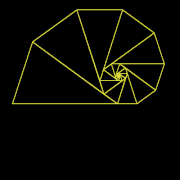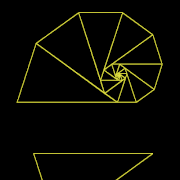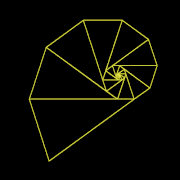
[ редактировать ]В остроугольном равнобедренном треугольнике можно нарисовать аналогичный треугольник, но меньшего размера, одна из сторон которого является основанием исходного треугольника. Гномоном этих двух подобных равнобедренных треугольников является треугольник, который останется, если меньший из двух подобных равнобедренных треугольников удалить из большего. Гномон сам является равнобедренным тогда и только тогда, когда отношение сторон к основанию исходного равнобедренного треугольника и отношение основания к сторонам гномона равно золотому сечению . В этом случае остроугольный равнобедренный треугольник является золотой треугольник и его гномон — золотой гномон . [4] И наоборот, острый золотой треугольник может быть гномоном тупого золотого треугольника при исключительном взаимном обмене ролями. [5]
- золотой треугольник разделен на золотой треугольник меньшего размера и (тупой) золотой гномон
- Тупоугольный золотой треугольник является гномоном остроугольного золотого треугольника.
- Острый золотой треугольник — гномон тупоугольного золотого треугольника.
- Острый золотой треугольник — гномон восьмиугольника.
- Тупой золотой треугольник — гномон эннеагона.
Метафора и символика
[ редактировать ]Метафора, основанная на геометрии гномона, играет важную роль в литературном анализе « » Джеймса Джойса , Дублинцев включая игру слов между «параличом» и «параллелограммом», а также геометрическое значение гномона как чего-то фрагментарного. уменьшилась в своей законченной форме. [6] [7] [8] [9]
Формы гномонов также заметны в «Арифметической композиции I» , абстрактной картине Тео ван Дусбурга . [10]
Также есть очень короткая иллюстрированная анимацией геометрическая сказка, где гномоны играют роль захватчиков. [11]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Газале, Мидхат Дж. (1999), «Гномон: от фараонов к фракталам», Европейский журнал физики , 20 (6), Princeton University Press: 523, Bibcode : 1999EJPh...20..523G , ISBN 9780691005140 .
- ^ Деза, Елена ; Деза, Мишель (2012), Образные числа , World Scientific, стр. 3, ISBN. 9789814355483 .
- ^ Роу, Т. Сундара (1893), Геометрические упражнения по складыванию бумаги , Мадрас: Аддисон, стр. 46–48 .
- ^ Леб, Артур Л. (1993), «Золотой треугольник», Концепции и изображения: визуальная математика , Коллекция Design Science, Springer, стр. 179–192, doi : 10.1007/978-1-4612-0343-8_20 , ISBN 978-1-4612-6716-4
- ^ Пьетрокола, Джорджио (2005). «Коллекция гномонов» . Маэкла .
- ^ Фридрих, Герхард (1957), «Гномонический ключ к дублинцам Джеймса Джойса», Modern Language Notes , 72 (6): 421–424, doi : 10.2307/3043368 , JSTOR 3043368 .
- ^ Вейр, Дэвид (1991), «Гномон - это остров: Евклид и Бруно в повествовательной практике Джойса», James Joyce Quarterly , 28 (2): 343–360, JSTOR 25485150 .
- ^ Фридрих, Герхард (1965), «Перспектива дублинцев Джойса», College English , 26 (6): 421–426, doi : 10.2307/373448 , JSTOR 373448 .
- ^ Райхерт, Клаус (1988), «Фрагмент и целостность» , Скотт, Бонни Кайм (редактор), «Новые альянсы в исследованиях Джойса: когда это подражает дельфийцу» , University of Delaware Press, стр. 86–87, ISBN 9780874133288
- ^ Виги, Паола; Аскьери, Игино (2010), «От искусства к математике в картинах Тео ван Дусбурга», в Капечки, Витторио; Бушема, Массимо; Контуччи, Пьерлуиджи; и др. (ред.), «Приложения математики в моделях, искусственных нейронных сетях и искусстве» , «Математика и общество», Springer, стр. 601–610, doi : 10.1007/978-90-481-8581-8_27 , ISBN 978-90-481-8580-1 .
- ^ Пьетрокола, Джорджио (2005). «Золотой король и нашествие гномонов» . Маэкла . .