Кановское расслоение

В математике комплексы Кана и расслоения Кана являются частью теории симплициальных множеств . Кановские расслоения представляют собой расслоения структуры категорий стандартной модели на симплициальных множествах и поэтому имеют фундаментальное значение. Кан-комплексы являются фибрантными объектами в этой модельной категории. Название в честь Дэниела Кана .

Определения

Определение стандартного n-симплекса

Полосатый синий симплекс в области должен существовать, чтобы это отображение было канновским расслоением.

Напомним, что для каждого n ≥ 0 стандарт $n$-симплекс , $\Delta ^{n}$, представляет собой представимое симплициальное множество

$\Delta ^{n}(i)=\mathrm {Hom} _{\mathbf {\Delta } }([i],[n])$

Применение функтора геометрической реализации к этому симплициальному множеству дает пространство, гомеоморфное топологическому стандарту. $n$-симплекс : выпуклое подпространство $\mathbb {R} ^{n+1}$ состоящий из всех точек $(t_{0},\dots ,t_{n})$ такие, что координаты неотрицательны и в сумме равны 1.

Определение рога

Основная статья: Рог симплекса

Для каждого k ≤ n это имеет подкомплекс $\Lambda _{k}^{n}$, k -й рог внутри $\Delta ^{n}$, соответствующий границе n -симплекса , с удаленной k -й гранью. Формально это можно определить разными способами, например, объединением изображений n карт. $\Delta ^{n-1}\rightarrow \Delta ^{n}$ соответствующий всем остальным граням $\Delta ^{n}$. Рога формы $\Lambda _{k}^{2}$ сидя внутри $\Delta ^{2}$выглядеть как черная буква V вверху соседнего изображения. Если $X$ является симплициальным множеством, то отображает

$s:\Lambda _{k}^{n}\to X$

соответствуют коллекциям $n$ $(n-1)$-симплексы, удовлетворяющие условию совместимости, по одному на каждый $0\leq k\leq n-1$. В явном виде это условие можно записать следующим образом. Написать $(n-1)$-упрощается в виде списка $(s_{0},\dots ,s_{k-1},s_{k+1},\dots ,s_{n})$ и требовать этого

$d_{i}s_{j}=d_{j-1}s_{i}\,$ для всех $i<j$ с $i,j\neq k$.

Эти условия выполняются для $(n-1)$-просто из $\Lambda _{k}^{n}$ сидя внутри $\Delta ^{n}$.

кановского

Диаграмма подъема кановского расслоения

Карта симплициальных множеств $f:X\rightarrow Y$ является кановским расслоением , если для любого $n\geq 1$ и $0\leq k\leq n$, и для любых карт $s:\Lambda _{k}^{n}\rightarrow X$ и $y:\Delta ^{n}\rightarrow Y\,$ такой, что $f\circ s=y\circ i$ (где $i$ это включение $\Lambda _{k}^{n}$ в $\Delta ^{n}$), существует карта $x:\Delta ^{n}\rightarrow X$ такой, что $s=x\circ i$ и $y=f\circ x$. Таким образом, определение очень похоже на определение расслоений в топологии (см. Также свойство подъема гомотопии ), откуда и произошло название «расслоение».

Технические замечания

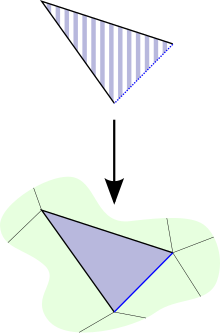
Используя переписку между $n$-симплексы симплициального множества $X$ и морфизмы $\Delta ^{n}\to X$(следствие леммы Йонеды ), это определение можно записать в терминах симплексов. Изображение карты $fs:\Lambda _{k}^{n}\to Y$можно рассматривать как рог, как описано выше. Спрашивая об этом $fs$ факторы через $yi$ соответствует требованию наличия $n$-симплекс в $Y$ чьи лица составляют рог из $fs$(вместе с еще одним лицом). Тогда искомая карта $x:\Delta ^{n}\to X$ соответствует симплексу в $X$ чьи лица включают рог из $s$. Диаграмма справа представляет собой пример в двух измерениях. Поскольку черная буква V на нижней диаграмме заполнена синей $2$-симплекс, если черная буква V выше соответствует ему, то полосатый синий $2$-симплекс должен существовать вместе с синим пунктиром $1$-симплекс, отображение очевидным образом.

определенные из кан

Симплициальный набор $X$ называется комплексом Кана , если отображение из $X\to \{*\}$, одноточечный симплициальный набор, является расслоением Кана. В категории моделей для симплициальных множеств $\{*\}$является терминальным объектом, поэтому комплекс Кана точно такой же, как фибрантный объект . Эквивалентно это можно сформулировать так: если каждая карта $\alpha :\Lambda _{k}^{n}\to X$ от рога имеет продолжение до $\Delta ^{n}$, это означает, что есть лифт ${\tilde {\alpha }}:\Delta ^{n}\to X$ такой, что

$\alpha ={\tilde {\alpha }}\circ \iota$

для карты включения $\iota :\Lambda _{k}^{n}\hookrightarrow \Delta ^{n}$, затем $X$представляет собой канский комплекс. И наоборот, каждый комплекс Кана обладает этим свойством, следовательно, оно дает простое техническое условие для комплекса Кана.

Примеры

Симплициальные множества

Важным примером является конструкция сингулярных симплексов , используемых для определения сингулярных гомологии , называемых сингулярным функтором. ^{стр. 7}

$S:{\text{Top}}\to s{\text{Sets}}$.

Учитывая пространство $X$, определить единственное число $n$-симплекс X является непрерывным отображением стандартной топологической $n$-симплекс (как описано выше) до $X$,

$f:\Delta _{n}\to X$

Взяв набор этих отображений для всех неотрицательных $n$ дает градуированный набор,

$S(X)=\coprod _{n}S_{n}(X)$.

Чтобы превратить это в симплициальный набор, определите карты граней $d_{i}:S_{n}(X)\to S_{n-1}(X)$ к

$(d_{i}f)(t_{0},\dots ,t_{n-1})=f(t_{0},\dots ,t_{i-1},0,t_{i},\dots ,t_{n-1})\,$

и карты вырождения $s_{i}:S_{n}(X)\to S_{n+1}(X)$ к

$(s_{i}f)(t_{0},\dots ,t_{n+1})=f(t_{0},\dots ,t_{i-1},t_{i}+t_{i+1},t_{i+2},\dots ,t_{n+1})\,$.

Поскольку союз любого $n+1$ лица $\Delta _{n+1}$ сильный деформационный ретракт представляет собой $\Delta _{n+1}$, любая непрерывная функция, определенная на этих гранях, может быть расширена до $\Delta _{n+1}$, что показывает, что $S(X)$ представляет собой канский комплекс.

геометрической

Стоит отметить, что сингулярный функтор правосопряжен с функтором геометрической реализации.

$|\cdot |:s{\text{Sets}}\to {\text{Top}}$

дающий изоморфизм

${\text{Hom}}_{\text{Top}}(|X|,Y)\cong {\text{Hom}}_{s{\text{Sets}}}(X,S(Y))$

Симплициальные множества, лежащие в основе симплициальных групп

Можно показать, что симплициальное множество, лежащее в основе симплициальной группы , всегда является фибрантным. ^{стр. 12} . В частности, для симплициальной абелевой группы ее геометрическая реализация гомотопически эквивалентна произведению пространств Эйленберга-Маклана.

$\prod _{i\in I}K(A_{i},n_{i})$

В частности, это включает в себя классификацию пространств . Итак, пространства $S^{1}\simeq K(\mathbb {Z} ,1)$, $\mathbb {CP} ^{\infty }\simeq K(\mathbb {Z} ,2)$, и бесконечные линзовые пространства $L_{q}^{\infty }\simeq K(\mathbb {Z} /q,2)$соответствуют комплексам Кана некоторого симплициального множества. Фактически, это множество можно построить явно, используя соответствие Долда – Кана цепного комплекса и взяв лежащий в основе симплициальный набор симплициальной абелевой группы.

малых

Другим важным источником примеров являются симплициальные множества, связанные с небольшим группоидом. ${\mathcal {G}}$. Это определяется как геометрическая реализация симплициального множества $[\Delta ^{op},{\mathcal {G}}]$ и обычно обозначается $B{\mathcal {G}}$. Мы могли бы также заменить ${\mathcal {G}}$с бесконечным группоидом. Выдвигается гипотеза, что гомотопическая категория геометрических реализаций группоидов бесконечности эквивалентна гомотопической категории гомотопических типов. Это называется гомотопической гипотезой.

Непример: стандартный n-симплекс

оказывается стандарт $n$-симплекс $\Delta ^{n}$ это не кан-комплекс ^{стр. 38} . Построение противоположного примера в целом можно найти, рассмотрев пример малой размерности, скажем $\Delta ^{1}$. Взяв карту $\Lambda _{0}^{2}\to \Delta ^{1}$ отправка

${\begin{matrix}[0,2]\mapsto [0,0]&[0,1]\mapsto [0,1]\end{matrix}}$

дает противоположный пример, поскольку его нельзя распространить на карту $\Delta ^{2}\to \Delta ^{1}$потому что карты должны сохранять порядок. Если бы была карта, ее пришлось бы отправить

${\begin{aligned}0\mapsto 0\\1\mapsto 1\\2\mapsto 0\end{aligned}}$

но это не карта симплициальных множеств.

Категориальные свойства

Симплициальное обогащение и функциональные комплексы

Для симплициальных множеств $X,Y$ существует связанный симплициальный набор, называемый функциональным комплексом ${\textbf {Hom}}(X,Y)$, где симплексы определяются как

${\textbf {Hom}}_{n}(X,Y)={\text{Hom}}_{s{\text{Sets}}}(X\times \Delta ^{n},Y)$

и для порядковой карты $\theta :[m]\to [n]$ существует индуцированное отображение

$\theta ^{*}:{\textbf {Hom}}(X,Y)_{n}\to {\textbf {Hom}}(X,Y)_{m}$

(поскольку первый фактор Hom контравариантен), определяемый отправкой карты $f:X\times \Delta ^{n}\to Y$ в состав

$X\times \Delta ^{m}\xrightarrow {1\times \theta } X\times \Delta ^{n}\xrightarrow {f} Y$

Экспоненциальный закон

Этот комплекс имеет следующий экспоненциальный закон симплициальных множеств

${\text{ev}}_{*}:{\text{Hom}}_{s{\text{Sets}}}(K,{\textbf {Hom}}(X,Y))\to {\text{Hom}}_{s{\text{Sets}}}(X\times K,Y)$

который отправляет карту $f:K\to {\textbf {Hom}}(X,Y)$ на составную карту

$X\times K\xrightarrow {1\times g} X\times {\textbf {Hom}}(X,Y)\xrightarrow {ev} Y$

где $ev(x,f)=f(x,\iota _{n})$ для $\iota _{n}\in {\text{Hom}}_{\Delta }([n],[n])$ поднят до n-симплекса $\Delta ^{n}$. ^

Кановские расслоения и обратные модели

Учитывая (Кан)-расслоение $p:X\to Y$ и включение симплициальных множеств $i:K\hookrightarrow L$, существует расслоение ^{стр. 21}

${\textbf {Hom}}(L,X)\xrightarrow {(i^{*},p_{*})} {\textbf {Hom}}(K,X)\times _{{\textbf {Hom}}(K,Y)}{\textbf {Hom}}(L,Y)$

(где ${\textbf {Hom}}$ находится в комплексе функций в категории симплициальных множеств), индуцированных из коммутативной диаграммы

${\begin{matrix}{\textbf {Hom}}(L,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(L,Y)\\i^{*}\downarrow &&\downarrow i^{*}\\{\textbf {Hom}}(K,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(K,Y)\end{matrix}}$

где $i^{*}$ это карта отката, заданная предварительной композицией и $p_{*}$— это карта продвижения вперед, заданная посткомпозицией. В частности, из предыдущего расслоения следует $p_{*}:{\textbf {Hom}}(L,X)\to {\textbf {Hom}}(L,Y)$ и $i^{*}:{\textbf {Hom}}(L,Y)\to {\textbf {Hom}}(K,Y)$ являются расслоениями.

Приложения

группы кан

Гомотопические группы фибрантного симплициального множества можно определить комбинаторно, используя рога, таким образом, чтобы это согласовывалось с гомотопическими группами реализующего его топологического пространства. Для комплекса Кан $X$ и вершина $x:\Delta ^{0}\to X$, как набор $\pi _{n}(X,x)$ определяется как набор карт $\alpha :\Delta ^{n}\to X$ симплициальных множеств, укладывающихся в некоторую коммутативную диаграмму:

$\pi _{n}(X,x)=\left\{\alpha :\Delta ^{n}\to X:{\begin{matrix}\Delta ^{n}&{\overset {\alpha }{\to }}&X\\\uparrow &&\uparrow x\\\partial \Delta ^{n}&\to &\Delta ^{0}\end{matrix}}\right\}$

Обратите внимание на тот факт $\partial \Delta ^{n}$ отображается в точку, эквивалентно определению сферы $S^{n}$ как частное $B^{n}/\partial B^{n}$ для стандартного единичного шара

$B^{n}=\{x\in \mathbb {R} ^{n}:||x||_{eu}\leq 1\}$

Определение структуры группы требует немного больше работы. По сути, учитывая две карты $\alpha ,\beta :\Delta ^{n}\to X$ есть связанный $(n+1)$- простой $\omega :\Delta ^{n+1}\to X$ такой, что $d_{n}\omega :\Delta ^{n}\to X$дает свое дополнение. Это отображение корректно определено с точностью до симплициальных гомотопических классов отображений, задающих структуру группы. Более того, группы $\pi _{n}(X,x)$ являются абелевыми для $n\geq 2$. Для $\pi _{0}(X)$, он определяется как гомотопические классы $[x]$ карт вершин $x:\Delta ^{0}\to X$.

симплициальных

Используя категории модели, любой симплициальный набор $X$ имеет фибрантную замену ${\hat {X}}$ что гомотопически эквивалентно $X$в гомотопической категории симплициальных множеств. Тогда гомотопические группы $X$ может быть определен как

$\pi _{n}(X,x):=\pi _{n}({\hat {X}},{\hat {x}})$

где ${\hat {x}}$ это лифт $x:\Delta ^{0}\to X$ к ${\hat {X}}$. Эти замены фибрантов можно рассматривать как топологический аналог резольвенты цепного комплекса (например, проективной резольвенты или плоской резольвенты ).

См. также

• Категория модели
• Симплициальная теория гомотопий
• Упрощенно обогащенная категория
• Слабый комплекс Кана (также называемый квазикатегорией, ∞-категорией)
• ∞-группоид
• Расслоение симплициальных множеств

Ссылки

• Элементарное иллюстрированное введение в симплициальные множества.

Библиография

• Гёрсс, Пол Г.; Джардин, Джон Ф. (1999). Симплициальная гомотопическая теория . Базель: Биркхойзер Базель. дои : 10.1007/978-3-0348-8707-6 . ISBN  978-3-0348-9737-2 . МР   1711612 .
• Мэй, Дж. Питер (1992) [1967]. Симплициальные объекты в алгебраической топологии . Чикагские лекции по математике. Чикаго, Иллинойс: Издательство Чикагского университета . ISBN  0-226-51180-4 . МР   1206474 .