Ро-алгоритм Полларда

Эта статья об алгоритме факторизации целых чисел. Для алгоритма дискретного логарифма см. Ро-алгоритм Полларда для логарифмов .

Ро-алгоритм Полларда — это алгоритм факторизации целых чисел . Его изобрел Джон Поллард в 1975 году. Он использует лишь небольшой объем пространства, а ожидаемое время его работы пропорционально квадратному корню из наименьшего простого множителя составного числа факторизуемого .

Основные идеи

Алгоритм используется для факторизации числа. $n=pq$, где $p$ является нетривиальным фактором. Полином по модулю $n$, называется $g(x)$ (например, $g(x)=(x^{2}+1){\bmod {n}}$), используется для генерации псевдослучайной последовательности . Важно отметить, что $g(x)$ должен быть полиномом. Выбирается начальное значение, скажем 2, и последовательность продолжается как $x_{1}=g(2)$, $x_{2}=g(g(2))$, $x_{3}=g(g(g(2)))$и т. д. Последовательность связана с другой последовательностью $\{x_{k}{\bmod {p}}\}$. С $p$ заранее не известна, эта последовательность не может быть явно вычислена в алгоритме. Однако именно в этом заключается основная идея алгоритма.

Поскольку число возможных значений для этих последовательностей конечно, оба $\{x_{k}\}$ последовательность, которая является модом $n$, и $\{x_{k}{\bmod {p}}\}$ последовательность в конечном итоге повторится, даже если эти значения неизвестны. Если бы последовательности вели себя как случайные числа, парадокс дня рождения подразумевал бы, что число $x_{k}$ до того, как произойдет повторение, как ожидается, будет $O({\sqrt {N}})$, где $N$ это количество возможных значений. Итак, последовательность $\{x_{k}{\bmod {p}}\}$ скорее всего, повторится намного раньше, чем последовательность $\{x_{k}\}$. Когда человек нашел $k_{1},k_{2}$ такой, что $x_{k_{1}}\neq x_{k_{2}}$ но $x_{k_{1}}\equiv x_{k_{2}}{\bmod {p}}$, число $|x_{k_{1}}-x_{k_{2}}|$ кратно $p$, так $p$ был найден.

Как только последовательность имеет повторяющееся значение, последовательность будет циклически повторяться, поскольку каждое значение зависит только от предыдущего. Эта структура возможного циклирования дала начало названию «алгоритм ро» из-за сходства с формой греческой буквы ρ, когда значения $x_{1}{\bmod {p}}$, $x_{2}{\bmod {p}}$и т. д. представлены как узлы ориентированного графа .

Диаграмма цикла, напоминающая греческую букву ρ.

Это обнаруживается алгоритмом поиска цикла Флойда : два узла $i$ и $j$ (т.е. $x_{i}$ и $x_{j}$) сохраняются. На каждом этапе один перемещается к следующему узлу в последовательности, а другой перемещается вперед на два узла. После этого проверяется, есть ли $\gcd(x_{i}-x_{j},n)\neq 1$. Если оно не равно 1, то это означает, что в $\{x_{k}{\bmod {p}}\}$ последовательность (т.е. $x_{i}{\bmod {p}}=x_{j}{\bmod {p}})$. Это работает, потому что, если $x_{i}$ то же самое, что $x_{j}$, разница между $x_{i}$ и $x_{j}$ обязательно кратно $p$. Хотя со временем это всегда происходит, результирующий наибольший общий делитель (НОД) является делителем $n$ кроме 1. Это может быть $n$ сам по себе, поскольку две последовательности могут повторяться одновременно. В этом (редком) случае алгоритм дает сбой и его можно повторить с другим параметром.

Алгоритм

Алгоритм принимает на вход n — , целое число подлежащее факторингу; и ⁠ $g(x)$⁠ , полином от x, вычисленный по модулю n . В исходном алгоритме $g(x)=(x^{2}-1){\bmod {n}}$, но в настоящее время чаще используют $g(x)=(x^{2}+1){\bmod {n}}$. Результатом является либо нетривиальный коэффициент n , либо сбой.

Он выполняет следующие шаги:

Псевдокод для алгоритма Ро Полларда

    x ← 2 // starting value
    y ← x
    d ← 1

    while d = 1:
        x ← g(x)
        y ← g(g(y))
        d ← gcd(|x - y|, n)

    if d = n: 
        return failure
    else:
        return d

Здесь x и y соответствуют ⁠ $x_{i}$⁠ и ⁠ $x_{j}$⁠ в предыдущем разделе. Обратите внимание, что этот алгоритм может не найти нетривиальный фактор, даже если n является составным. В этом случае метод можно попробовать еще раз, используя начальное значение x, отличное от 2 ( $0\leq x<n$) или другой ⁠ $g(x)$⁠ , $g(x)=(x^{2}+b){\bmod {n}}$, с $1\leq b<n-2$.

Пример факторизации

Позволять $n=8051$ и $g(x)=(x^{2}+1){\bmod {8}}051$.

Пример факторизации алгоритма Ро Полларда для $n=253$ и $g(x)=x^{2}{\bmod {2}}53$, с начальным значением 2. В примере используется алгоритм поиска цикла Флойда .

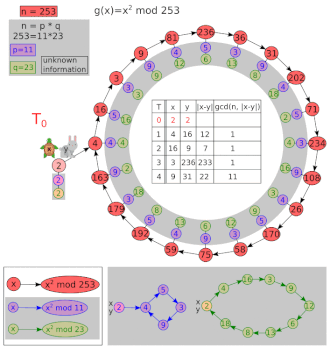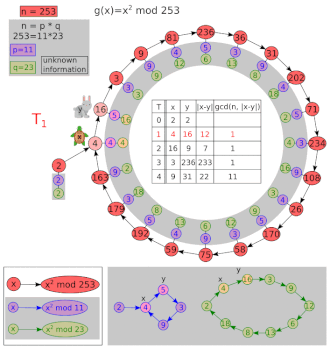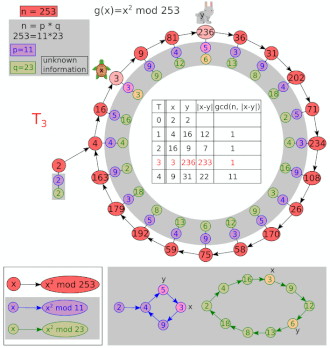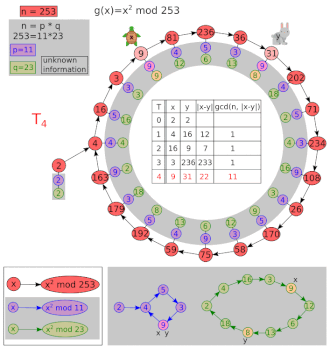
я	х	и	НОД(| х - у |, 8051)
1	5	26	1
2	26	7474	1
3	677	871	97
4	7474	1481	1

Теперь 97 — это нетривиальный коэффициент 8051. Начальные значения, отличные от x = y = 2, могут дать кофактор (83) вместо 97. Выше показана одна дополнительная итерация, чтобы прояснить, что y движется в два раза быстрее, чем x . Обратите внимание, что даже после повторения НОД может вернуться к 1.

Варианты

В 1980 году Ричард Брент опубликовал более быстрый вариант алгоритма ро. Он использовал те же основные идеи, что и Поллард, но другой метод обнаружения цикла, заменив алгоритм поиска цикла Флойда соответствующим методом поиска цикла Брента .

Дальнейшее улучшение было сделано Поллардом и Брентом. Они заметили, что если $\gcd(a,n)>1$, тогда также $\gcd(ab,n)>1$ для любого положительного целого числа ⁠ $b$⁠ . В частности, вместо вычисления $\gcd(|x-y|,n)$ на каждом шаге достаточно определить ⁠ $z$⁠ как произведение 100 последовательных $|x-y|$ условия по модулю ⁠ $n$⁠ , а затем вычислить одно $\gcd(z,n)$. Значительное ускорение достигается за счет НОД замены 100 шагов на 99 умножений по модулю ⁠ $n$⁠ и один НОД . Иногда это может привести к сбою алгоритма из-за введения повторяющегося фактора, например, когда ⁠ $n$⁠ — квадрат . Но тогда достаточно вернуться к предыдущему члену НОД , где $\gcd(z,n)=1$ используйте обычный алгоритм ρ и оттуда .

Приложение

Алгоритм очень быстр для чисел с небольшими факторами, но медленнее в случаях, когда все факторы большие. Самым выдающимся успехом алгоритма ρ стала факторизация числа Ферма в 1980 году F ₈ = 1238926361552897 × 934616397153579777769163558199606896584051237541638188580280321. Алгоритм ρ оказался хорошим выбором для F _8, поскольку простой множитель p = 1238926361552897 намного меньше другого множителя. Факторизация заняла 2 часа на UNIVAC 1100/42 .

Пример: факторинг n = 10403 = 101 · 103

В следующей таблице показаны числа, полученные алгоритмом, начиная с $x=2$ и используя полином $g(x)=(x^{2}+1){\bmod {1}}0403$. Третий и четвертый столбцы таблицы содержат дополнительную информацию, не известную алгоритму. Они включены, чтобы показать, как работает алгоритм.

⁠ $x$⁠	⁠ $y$⁠	⁠ $x{\bmod {1}}01$⁠	⁠ $y{\bmod {1}}01$⁠	шаг
2	2	2	2	0
5	2	5	2	1
26	2	26	2	2
677	26	71	26	3
598	26	93	26	4
3903	26	65	26	5
3418	26	85	26	6
156	3418	55	85	7
3531	3418	97	85	8
5168	3418	17	85	9
3724	3418	88	85	10
978	3418	69	85	11
9812	3418	15	85	12
5983	3418	24	85	13
9970	3418	72	85	14
236	9970	34	72	15
3682	9970	46	72	16
2016	9970	97	72	17
7087	9970	17	72	18
10289	9970	88	72	19
2594	9970	69	72	20
8499	9970	15	72	21
4973	9970	24	72	22
2799	9970	72	72	23

Первое повторение по модулю 101 равно 97, что происходит на шаге 17. Повторение не обнаруживается до шага 23, когда $x\equiv y{\pmod {101}}$. Это вызывает $\gcd(x-y,n)=\gcd(2799-9970,n)$ быть $p=101$, и фактор найден.

Сложность

Если псевдослучайное число $x=g(x)$ происходящие в алгоритме Полларда ρ, были реальным случайным числом, из этого следовало бы, что успех будет достигнут в половине случаев из-за парадокса дня рождения в $O({\sqrt {p}})\leq O(n^{1/4})$ итерации. Считается, что тот же анализ применим и к реальному алгоритму ро, но это эвристическое утверждение, и строгий анализ алгоритма остается открытым.

См. также

• Ро-алгоритм Полларда для логарифмов
• Алгоритм кенгуру Полларда

Дальнейшее чтение

• Бай, Ши; Брент, Ричард П. (январь 2008 г.). «Об эффективности метода Ро Полларда для дискретных логарифмов» . Конференции по исследованиям и практике в области информационных технологий, Vol. 77 . Австралазийский теоретический симпозиум (CATS2008). Вуллонгонг. стр. 125–131. Описывает улучшения, доступные благодаря различным итерационным функциям и алгоритмам поиска циклов.
• Кац, Джонатан; Линделл, Иегуда (2007). «Глава 8». Введение в современную криптографию . ЦРК Пресс.
• Сэмюэл С. Вагстафф-младший (2013). Радость факторинга . Провиденс, Род-Айленд: Американское математическое общество. стр. 135–138. ISBN  978-1-4704-1048-3 .

Внешние ссылки

• Подробная статья об алгоритме Ро Полларда, предназначенная для аудитории начального уровня.
• Вайсштейн, Эрик В. «Метод факторизации Полларда Ро» . Математический мир .
• Java-реализация
• О Полларде Ро