Числовая апертура

В оптике числовая апертура ( NA ) оптической системы — безразмерное число , характеризующее диапазон углов, в которых система может принимать или излучать свет. Благодаря включению показателя преломления в определение NA обладает свойством, заключающимся в том, что он постоянен для луча при переходе от одного материала к другому при условии отсутствия преломляющей силы на границе раздела. Точное определение этого термина немного различается в разных областях оптики. Числовая апертура обычно используется в микроскопии для описания приемного конуса объектива ( и, следовательно, его светосиловой способности и разрешения ), а также в волоконной оптике , где она описывает диапазон углов, в пределах которых свет, падающий на волокно, будет передаваться по нему.

Общая оптика

В большинстве областей оптики, и особенно в микроскопии , числовая апертура оптической системы, такой как объектив, определяется выражением

$\mathrm {NA} =n\sin \theta ,$

где $n$ — показатель преломления среды, в которой работает линза (1,00 для воздуха , 1,33 для чистой воды и обычно 1,52 для иммерсионного масла ; ^{[ 1 ]} см. также список показателей преломления ), а $θ$ — половина угла максимального светового конуса, который может войти или выйти из линзы. В общем, это угол реального краевого луча в системе. Поскольку показатель преломления включен, числовая апертура пучка лучей является инвариантом, поскольку пучок лучей проходит из одного материала в другой через плоскую поверхность. Это легко показать, изменив закон Снелла и обнаружив, что $n sin θ$ постоянно на границе интерфейса.

На воздухе угловая апертура линзы примерно вдвое превышает эту величину (в параксиальном приближении ). Числовая апертура обычно измеряется относительно конкретного объекта или точки изображения и будет меняться по мере перемещения этой точки. В микроскопии NA обычно относится к числовой апертуре пространства объекта, если не указано иное.

В микроскопии числовая апертура важна, поскольку она указывает на разрешающую способность линзы. Размер мельчайших деталей, которые можно разрешить ( разрешение ), пропорционален $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ λ / 2NA ⁠$ , где $λ$ — длина волны света. Объектив с большей числовой апертурой сможет визуализировать более мелкие детали, чем объектив с меньшей числовой апертурой. Предполагая качественную ( ограниченную дифракцией ) оптику, линзы с большей числовой апертурой собирают больше света и, как правило, обеспечивают более яркое изображение, но обеспечивают меньшую глубину резкости .

Числовая апертура используется для определения «размера ямы» в форматах оптических дисков . ^{[ 2 ]}

Увеличение увеличения и числовой апертуры объектива уменьшает рабочее расстояние, т.е. расстояние между передней линзой и образцом.

Числовая апертура в зависимости от числа f

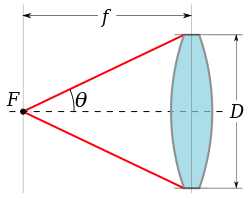
Числовая апертура обычно не используется в фотографии . Вместо этого угловая апертура объектива ( или зеркала изображения) выражается числом f , записанным f / N , где $N$ — f-число, определяемое отношением фокусного расстояния $f$ к диаметру входного зрачка $D$ :

$N={\frac {f}{D}}.$

Это соотношение связано с числовой апертурой пространства изображения, когда объектив фокусируется на бесконечности. ^{[ 3 ]} Судя по диаграмме справа, числовая апертура объектива в пространстве изображения равна:

${\text{NA}}_{\text{i}}=n\sin \theta =n\sin \left[\arctan \left({\frac {D}{2f}}\right)\right]\approx n{\frac {D}{2f}},$

таким образом, $N \approx ⁠ 1 / 2NA i ⁠$ при условии нормального использования на воздухе ( $n = 1$ ).

Приближение справедливо, когда числовая апертура мала, но оказывается, что для хорошо скорректированных оптических систем, таких как фотообъективы, более детальный анализ показывает, что $N$ почти точно равно $1/(2NA i)$ даже при больших числовых апертурах. Как объясняет Рудольф Кингслейк: «Это распространенная ошибка — предполагать, что отношение [ $D /2 f$ ] на самом деле равно $tan θ$ , а не $sin θ$ … Касательная, конечно, была бы правильной, если бы главные плоскости были на самом деле плоскость. Однако полная теория условия синуса Аббе показывает, что если в объектив внести поправку на кому и сферическую аберрацию , как и должно быть у всех хороших фотографических объективов, вторая главная плоскость становится частью сферы радиуса $f.$ сосредоточен вокруг фокуса». ^{[ 4 ]} В этом смысле традиционное определение тонкой линзы и иллюстрация числа f вводят в заблуждение, и определение его с точки зрения числовой апертуры может быть более значимым.

Рабочее (эффективное) число f

Число f описывает светособирающую способность линзы в случае, когда краевые лучи со стороны объекта параллельны оси линзы. Этот случай часто встречается в фотографии, где фотографируемые объекты часто находятся далеко от камеры. объектива Однако, когда объект не находится далеко от объектива, изображение больше не формируется в фокальной плоскости , и число f больше не точно описывает светосилу объектива или числовую апертуру на стороне изображения. В этом случае числовая апертура связана с тем, что иногда называют « рабочим числом f » или «эффективным числом f».

Рабочее число f определяется путем изменения приведенного выше соотношения с учетом увеличения от объекта к изображению:

${\frac {1}{2{\text{NA}}_{\text{i}}}}=N_{\text{w}}=\left(1-{\frac {m}{P}}\right)N,$

где $N w$ — рабочее число f, $m$ объектива — увеличение для объекта, находящегося на определенном расстоянии, $P$ — увеличение зрачка , а NA определяется как угол краевого луча, как и раньше. ^{[ 3 ]}^{[ 5 ]} Увеличение здесь обычно отрицательное, а увеличение зрачка чаще всего принимается равным 1 — как объясняет Аллен Р. Гринлиф: «Освещенность изменяется обратно пропорционально квадрату расстояния между выходным зрачком линзы и положением пластинки или пластины. Поскольку положение выходного зрачка обычно неизвестно пользователю объектива, вместо него используется заднее сопряженное фокусное расстояние; возникающая таким образом теоретическая ошибка незначительна для большинства типов фотообъективов». ^{[ 6 ]}

В фотографии коэффициент иногда записывают как $1 + m$ , где $m$ представляет собой абсолютное значение увеличения; в любом случае поправочный коэффициент равен 1 или больше. Каждое из двух равенств в приведенном выше уравнении используется разными авторами в качестве определения рабочего числа f, как иллюстрируют цитируемые источники. Они не обязательно оба точны, но часто к ним относятся так, как будто они точны.

И наоборот, числовая апертура на стороне объекта связана с числом f посредством увеличения (стремящегося к нулю для удаленного объекта):

${\frac {1}{2{\text{NA}}_{\text{o}}}}={\frac {m-P}{mP}}N.$

Лазерная физика

В лазерной физике числовая апертура определяется несколько иначе. Лазерные лучи распространяются по мере распространения, но медленно. Вдали от самой узкой части луча распространение примерно линейно зависит от расстояния — лазерный луч образует конус света в «дальнем поле». Соотношение, используемое для определения числовой апертуры лазерного луча, такое же, как и для оптической системы:

${\text{NA}}=n\sin \theta ,$

но $θ$ определяется по-другому. Лазерные лучи обычно не имеют острых краев, как конус света, проходящий через апертуру линзы . Вместо этого интенсивность излучения постепенно падает по мере удаления от центра луча. Очень часто луч имеет гауссов профиль. Лазерные физики обычно предпочитают считать $луча$ : θ расходимостью углом в дальнем поле между осью луча и расстоянием от оси, на котором интенсивность излучения падает до $e. -2$ раз больше осевого излучения. Тогда числовая апертура гауссова лазерного луча связана с его минимальным размером пятна («перетяжкой луча») соотношением

${\text{NA}}\simeq {\frac {\lambda _{0}}{\pi w_{0}}},$

где $λ 0$ — вакуумная длина волны света, а $2 w 0$ — диаметр луча в самом узком месте, измеренный между $e -2$ точки облучения («Полная ширина при $e -2$ максимум интенсивности"). Это означает, что лазерный луч, сфокусированный в небольшом пятне, будет быстро распространяться по мере удаления от фокуса, в то время как лазерный луч большого диаметра может оставаться примерно того же размера на очень большом расстоянии. См. также: Ширина гауссова луча .

Волоконная оптика

Многомодовое оптическое волокно будет распространять свет, попадающий в волокно, только в определенном диапазоне углов, известном как приемный конус волокна. Полуугол этого конуса называется приемным углом , $θ max$ . Для ступенчатого многомодового волокна в данной среде приемный угол определяется только показателями преломления сердцевины, оболочки и среды: $n\sin \theta _{\max }={\sqrt {n_{\text{core}}^{2}-n_{\text{clad}}^{2}}},$ где $n$ — показатель преломления среды вокруг волокна, $n core$ — показатель преломления сердцевины волокна, а $n clad$ — показатель преломления оболочки . Хотя сердцевина будет принимать свет под большими углами, эти лучи не будут полностью отражаться от границы раздела сердцевина-оболочка и поэтому не будут передаваться на другой конец волокна. Вывод этой формулы приведен ниже.

Когда луч света падает из среды с показателем преломления $n$ с показателем $n в ядро$ под максимальным углом принятия, закон Снелла на границе раздела среда-ядро дает $n\sin \theta _{\max }=n_{\text{core}}\sin \theta _{r}.\$

Из геометрии приведенного выше рисунка имеем: $\sin \theta _{r}=\sin \left({90^{\circ }}-\theta _{c}\right)=\cos \theta _{c}$

где $\theta _{c}=\arcsin {\frac {n_{\text{clad}}}{n_{\text{core}}}}$

– критический угол полного внутреннего отражения .

Заменив $cos θ c$ на $sin θ r$ в законе Снеллиуса, получим: ${\frac {n}{n_{\text{core}}}}\sin \theta _{\max }=\cos \theta _{c}.$

Возведя в квадрат обе стороны ${\frac {n^{2}}{n_{\text{core}}^{2}}}\sin ^{2}\theta _{\max }=\cos ^{2}\theta _{c}=1-\sin ^{2}\theta _{c}=1-{\frac {n_{\text{clad}}^{2}}{n_{\text{core}}^{2}}}.$

Решая, находим формулу, указанную выше:

$n\sin \theta _{\max }={\sqrt {n_{\text{core}}^{2}-n_{\text{clad}}^{2}}},$

Она имеет ту же форму, что и числовая апертура в других оптических системах, поэтому стало обычным определять числовую апертуру любого типа волокна как $\mathrm {NA} ={\sqrt {n_{\text{core}}^{2}-n_{\text{clad}}^{2}}},$

где $n core$ — показатель преломления вдоль центральной оси волокна. Обратите внимание, что при использовании этого определения связь между числовой апертурой и приемным углом волокна становится лишь приближением. В частности, определение « NA », определенное таким образом, не применимо к одномодовому волокну . ^{[ 7 ]}^{[ 8 ]} Нельзя определить угол приема одномодового волокна, основываясь только на показателях преломления.

Число связанных мод , объем моды , связано с нормированной частотой и, следовательно, с числовой апертурой.

термин «равновесная числовая апертура» В многомодовых волокнах иногда используется . Это относится к числовой апертуре относительно крайнего угла выхода луча, выходящего из волокна, в котором равновесное распределение мод установлено .

См. также

f-число
Запуск числовой апертуры
Направляемый луч , оптоволокна контекст
Угол приема (солнечный концентратор) , дальнейший контекст

Ссылки

^ Каргилл, Джон Дж. (1985). «Иммерсионное масло и микроскоп» (PDF) (2-е изд.). Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 16 октября 2019 г.
^ «Обновление диска высокой четкости: положение дел с HD DVD и Blu-ray». Архивировано 10 января 2008 г. в Wayback Machine Стивом Киндигом, консультантом Crutchfield . По состоянию на 18 января 2008 г.
^ Jump up to: ^а ^б Грейвекамп, Джон Э. (2004). Полевое руководство по геометрической оптике . Полевые руководства SPIE. Том. ФГ01. ШПИОН. стр. 29. ISBN 0-8194-5294-7 .
^ Рудольф Кингслейк (1951). Объективы в фотографии: практическое руководство по оптике для фотографов . Кейс-Хойт, для Garden City Books. стр. 97–98.
^ Арекки, Анджело В.; Мессади, Тахар и Кошель, Р. Джон (2007). Полевое руководство по освещению . ШПИОН. п. 48. ИСБН 978-0-8194-6768-3 .
^ Гринлиф, Аллен Р. (1950). Фотооптика . Компания Макмиллан. п. 24.
^ Пашотта, Р. «Цифровая апертура» . Энциклопедия фотоники RP . дои : 10.61835/fov . Проверено 25 августа 2024 г.
^ Ковалевич-младший, Эндрю М.; Бухольц, Фрэнк (6 октября 2006 г.). Расходимость луча оптического волокна SMF-28 (Отчет). Военно-морская исследовательская лаборатория. НРЛ/МР/5650-06-8996.

В этой статье использованы общедоступные материалы из Федеральный стандарт 1037C . Управление общего обслуживания . Архивировано из оригинала 22 января 2022 г. (в поддержку MIL-STD-188 ).

Внешние ссылки

«Цели микроскопа: числовая апертура и разрешение» , Мортимер Абрамовиц и Майкл В. Дэвидсон, «Молекулярные выражения: учебник по оптической микроскопии» (веб-сайт), Университет штата Флорида , 22 апреля 2004 г.
«Основные понятия и формулы в микроскопии: числовая апертура» , Майкл В. Дэвидсон, Nikon MicrocracyU (веб-сайт).
«Численная апертура» , Энциклопедия лазерной физики и техники (сайт).
«Численная апертура и разрешение» , Калифорнийского университета в Лос-Анджелесе Основные объекты микроскопии Института исследования мозга (веб-сайт), 2007.

[1] Каргилл, Джон Дж. (1985). «Иммерсионное масло и микроскоп» (PDF) (2-е изд.). Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 16 октября 2019 г.

[Crutchfield_Advisor-2] «Обновление диска высокой четкости: положение дел с HD DVD и Blu-ray». Архивировано 10 января 2008 г. в Wayback Machine Стивом Киндигом, консультантом Crutchfield . По состоянию на 18 января 2008 г.

[Greivenkamp-3] Jump up to: ^а ^б Грейвекамп, Джон Э. (2004). Полевое руководство по геометрической оптике . Полевые руководства SPIE. Том. ФГ01. ШПИОН. стр. 29. ISBN 0-8194-5294-7 .

[4] Рудольф Кингслейк (1951). Объективы в фотографии: практическое руководство по оптике для фотографов . Кейс-Хойт, для Garden City Books. стр. 97–98.

[5] Арекки, Анджело В.; Мессади, Тахар и Кошель, Р. Джон (2007). Полевое руководство по освещению . ШПИОН. п. 48. ИСБН 978-0-8194-6768-3 .

[6] Гринлиф, Аллен Р. (1950). Фотооптика . Компания Макмиллан. п. 24.

[7] Пашотта, Р. «Цифровая апертура» . Энциклопедия фотоники RP . дои : 10.61835/fov . Проверено 25 августа 2024 г.

[8] Ковалевич-младший, Эндрю М.; Бухольц, Фрэнк (6 октября 2006 г.). Расходимость луча оптического волокна SMF-28 (Отчет). Военно-морская исследовательская лаборатория. НРЛ/МР/5650-06-8996.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]