✖


Jump to content

Метаэвристический

(Перенаправлено с Мета-алгоритма )

В информатике и математической оптимизации метаэвристика — это более высокого уровня процедура или эвристика , предназначенная для поиска, генерации, настройки или выбора эвристики ( алгоритма частичного поиска ), которая может обеспечить достаточно хорошее решение проблемы оптимизации или машинного обучения задачи . , особенно при неполной или неполной информации или ограниченной вычислительной мощности. [1] [2] Метаэвристика выбирает подмножество решений, которое в противном случае слишком велико, чтобы его можно было полностью перечислить или исследовать иным образом. Метаэвристика может делать относительно мало предположений о решаемой задаче оптимизации и поэтому может использоваться для решения множества задач. [3]

По сравнению с алгоритмами оптимизации и итерационными методами метаэвристика не гарантирует, что глобально оптимальное решение . для некоторого класса задач можно найти [3] Многие метаэвристики реализуют ту или иную форму стохастической оптимизации , так что найденное решение зависит от набора сгенерированных случайных величин . [2] В комбинаторной оптимизации , путем поиска по большому набору возможных решений , метаэвристика часто может найти хорошие решения с меньшими вычислительными затратами, чем алгоритмы оптимизации, итеративные методы или простые эвристики. [3] По существу, они являются полезными подходами к решению задач оптимизации. [2] По этой теме было опубликовано несколько книг и обзорных статей. [2] [3] [4] [5] [6] Обзор литературы по метаэвристической оптимизации, [7] предположил, что именно Фред Гловер придумал слово «метаэвристика». [8]

Большая часть литературы по метаэвристике носит экспериментальный характер и описывает эмпирические результаты, основанные на компьютерных экспериментах с алгоритмами. Но доступны и некоторые формальные теоретические результаты, часто касающиеся сходимости и возможности нахождения глобального оптимума. [3] Многие метаэвристические методы были опубликованы с заявлениями о новизне и практической эффективности. Хотя в этой области также проводятся высококачественные исследования, многие публикации были низкого качества; недостатки включают неясность, отсутствие концептуальной разработки, плохие эксперименты и незнание предыдущей литературы. [9]

Характеристики

[ редактировать ]

Это свойства, которые характеризуют большинство метаэвристик: [3]

  • Метаэвристика — это стратегии, которые направляют процесс поиска.
  • Цель состоит в том, чтобы эффективно исследовать пространство поиска, чтобы найти почти оптимальные решения.
  • Методы, составляющие метаэвристические алгоритмы, варьируются от простых процедур локального поиска до сложных процессов обучения.
  • Метаэвристические алгоритмы являются приблизительными и обычно недетерминированными.
  • Метаэвристика не ориентирована на конкретную проблему.

Классификация

[ редактировать ]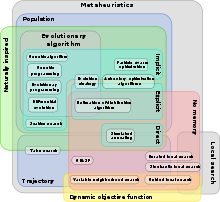
Диаграмма Эйлера различных классификаций метаэвристики. [10]

Существует большое разнообразие метаэвристик. [2] и ряд свойств, по которым их можно классифицировать. [3]

[ редактировать ]

Один из подходов заключается в характеристике типа стратегии поиска. [3] Одним из типов стратегии поиска является усовершенствование простых алгоритмов локального поиска. Хорошо известным алгоритмом локального поиска является метод восхождения на холм , который используется для поиска локальных оптимумов. Однако подъем в гору не гарантирует нахождения глобальных оптимальных решений.

Было предложено множество метаэвристических идей для улучшения эвристики локального поиска с целью нахождения лучших решений. К таким метаэвристикам относятся моделирование отжига , поиск с запретами , итерационный локальный поиск , поиск по переменной окрестности и GRASP . [3] Эти метаэвристики можно классифицировать как метаэвристики локального поиска или метаэвристики глобального поиска.

Другая метаэвристика глобального поиска, не основанная на локальном поиске, обычно представляет собой метаэвристику на основе совокупности . Такая метаэвристика включает оптимизацию колонии муравьев , эволюционные вычисления, такие как генетический алгоритм или стратегии эволюции , оптимизацию роя частиц , алгоритм оптимизации наездника. [11] и алгоритм бактериального поиска пищи. [12]

Единое решение или популяционное решение

[ редактировать ]

Еще одним параметром классификации является сравнение одного решения и поиска на основе совокупности . [3] [6] Подходы к единому решению направлены на изменение и улучшение единственного решения-кандидата; Метаэвристика единого решения включает моделируемый отжиг , итерационный локальный поиск , поиск по переменной окрестности и управляемый локальный поиск . [6] Подходы, основанные на популяционном подходе, поддерживают и улучшают множество возможных решений, часто используя характеристики населения для руководства поиском; Метаэвристика, основанная на популяциях, включает эволюционные вычисления и оптимизацию роя частиц . [6] Другая категория метаэвристики — это роевой интеллект , который представляет собой коллективное поведение децентрализованных, самоорганизующихся агентов в популяции или рое. Оптимизация колонии муравьев , [13] оптимизация роя частиц , [6] социальная когнитивная оптимизация и алгоритм бактериального поиска пищи [12] являются примерами этой категории.

Гибридизация и меметические алгоритмы

[ редактировать ]

Гибридная метаэвристика — это та, которая сочетает в себе метаэвристику с другими подходами к оптимизации, такими как алгоритмы математического программирования , программирования в ограничениях и машинного обучения . Оба компонента гибридной метаэвристики могут работать одновременно и обмениваться информацией для руководства поиском.

С другой стороны, меметические алгоритмы [14] представляют собой синергию эволюционного или любого популяционного подхода с отдельными процедурами индивидуального обучения или местного улучшения для поиска проблем. Примером меметического алгоритма является использование алгоритма локального поиска вместо или в дополнение к базовому оператору мутации в эволюционных алгоритмах.

Параллельная метаэвристика

[ редактировать ]

Параллельная метаэвристика — это та, которая использует методы параллельного программирования для параллельного выполнения нескольких метаэвристических поисков; они могут варьироваться от простых распределенных схем до параллельных поисков, которые взаимодействуют для улучшения общего решения.

Метаэвристика, вдохновленная природой и основанная на метафорах

[ редактировать ]
Основные статьи: Роевой интеллект и Список метаэвристик, основанных на метафорах.

Очень активной областью исследований является разработка природной метаэвристики. Многие современные метаэвристики, особенно эволюционные алгоритмы, основанные на вычислениях, вдохновлены природными системами. Природа выступает источником концепций, механизмов и принципов проектирования искусственных вычислительных систем для решения сложных вычислительных задач. Такая метаэвристика включает моделирование отжига , эволюционные алгоритмы , оптимизацию колоний муравьев и оптимизацию роя частиц . Большое количество более поздних метаэвристик, вдохновленных метафорами, начали вызывать критику в исследовательском сообществе за то, что они скрывают отсутствие новизны за сложной метафорой. [9]

Приложения

[ редактировать ]

Метаэвристика используется для всех типов задач оптимизации: от непрерывных и смешанных целочисленных задач до комбинаторной оптимизации или их комбинаций. При комбинаторной оптимизации оптимальное решение ищется в дискретном пространстве поиска. Примером проблемы является задача коммивояжера , где пространство поиска возможных решений растет быстрее, чем экспоненциально , по мере увеличения размера проблемы, что делает исчерпывающий поиск оптимального решения невозможным. Кроме того, многомерные комбинаторные задачи, включая большинство задач проектирования в технике. [15] [16] [17] такие как поиск формы и поиск поведения, страдают от проклятия размерности , что также делает их невозможными для исчерпывающего поиска или аналитических методов .

Метаэвристика также часто применяется для решения задач планирования. Типичным представителем этого комбинаторного класса задач является цеховое планирование, которое предполагает назначение этапов выполнения работ станциям обработки таким образом, чтобы все работы выполнялись вовремя и в целом в кратчайшие сроки. [18] [19] На практике часто приходится соблюдать ограничения, например, ограничивая допустимую последовательность рабочих этапов задания с помощью заранее определенных рабочих процессов. [20] и/или в отношении использования ресурсов, например, в форме сглаживания спроса на энергию. [21] [22] Популярные метаэвристики для комбинаторных задач включают генетические алгоритмы Холланда и др., [23] разбросанный поиск [24] и табу-поиск [25] от Гловера.

Еще одна большая область применения — задачи оптимизации в пространствах непрерывного или смешанно-целочисленного поиска. Сюда входит, например, оптимизация конструкции. [26] [27] [28] или различные инженерные задачи. [29] [30] [31] Примером сочетания комбинаторной и непрерывной оптимизации является планирование благоприятных траекторий движения промышленных роботов. [32] [33]

Механизмы метаэвристической оптимизации

[ редактировать ]

MOF можно определить как «набор программных инструментов, которые обеспечивают правильную и многократно используемую реализацию набора метаэвристик, а также базовые механизмы для ускорения реализации подчиненных эвристик партнера (возможно, включая кодировки решения и операторы, специфичные для метода). , которые необходимы для решения конкретного экземпляра проблемы с использованием предоставленных методов». [34]

Существует множество потенциальных инструментов оптимизации, которые можно рассматривать как MOF с различными характеристиками: Comet, EvA2, evolvica, Evolutionary::Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO. , Пиза, Часовщик, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Набор инструментов алгоритма оптимизации, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA, Metaheuristics.jl, UOF [34] и ОптаПланнер.

Взносы

[ редактировать ]

Существует множество различных метаэвристик, и постоянно предлагаются новые варианты. Некоторые из наиболее значительных вкладов в эту область:

См. также

[ редактировать ]

Ссылки

[ редактировать ]
  1. ^ Р. Баламуруган; А. М. Натараджан; К. Премалатха (2015). «Оптимизация черной дыры звездной массы для бикластеризации данных об экспрессии генов на микрочипах» . Прикладной искусственный интеллект . 29 (4): 353–381. дои : 10.1080/08839514.2015.1016391 . S2CID   44624424 .
  2. ^ Jump up to: а б с д и Бьянки, Леонора; Марко Дориго; Лука Мария Гамбарделла; Уолтер Дж. Гутяр (2009). «Обзор метаэвристики для стохастической комбинаторной оптимизации» (PDF) . Естественные вычисления . 8 (2): 239–287. дои : 10.1007/s11047-008-9098-4 . S2CID   9141490 .
  3. ^ Jump up to: а б с д и ж г час я дж Блюм, К.; Роли, А. (2003). «Метаэвристика в комбинаторной оптимизации: обзор и концептуальное сравнение» . 35 (3). Обзоры вычислительной техники ACM: 268–308. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
  4. ^ Гольдберг, Делавэр (1989). Генетические алгоритмы в поиске, оптимизации и машинном обучении . Академическое издательство Клювер. ISBN  978-0-201-15767-3 .
  5. ^ Гловер, Ф.; Кохенбергер, Джорджия (2003). Справочник по метаэвристике . Том. 57. Спрингер, Международная серия по исследованию операций и науке управления. ISBN  978-1-4020-7263-5 .
  6. ^ Jump up to: а б с д и Талби, Э.Г. (2009). Метаэвристика: от проектирования к реализации . Уайли. ISBN  978-0-470-27858-1 .
  7. ^ XS Ян, Метаэвристическая оптимизация, Scholarpedia, 6 (8): 11472 (2011).
  8. ^ Гловер Ф., (1986). Будущие пути целочисленного программирования и связи с искусственным интеллектом , Computers and Operations Research, 13, 533–549 (1986).
  9. ^ Jump up to: а б Соренсен, Кеннет (2015). «Метаэвристика — раскрытая метафора» (PDF) . Международные сделки в области операционных исследований . 22 :3–18. CiteSeerX   10.1.1.470.3422 . дои : 10.1111/itor.12001 . S2CID   14042315 . Архивировано из оригинала (PDF) 2 ноября 2013 г.
  10. ^ Классификация метаэвристики
  11. ^ Д, Бину (2019). «RideNN: новая нейронная сеть на основе алгоритма оптимизации Rider для диагностики неисправностей в аналоговых схемах» . Транзакции IEEE по приборостроению и измерениям . 68 (1): 2–26. Бибкод : 2019ITIM...68....2B . дои : 10.1109/TIM.2018.2836058 . S2CID   54459927 .
  12. ^ Jump up to: а б Панг, Шинсион; Чен, Му-Чен (1 июня 2023 г.). «Оптимизация расписания работы железнодорожных бригад с помощью модифицированного алгоритма поиска бактерий» . Компьютеры и промышленная инженерия . 180 : 109218. doi : 10.1016/j.cie.2023.109218 . ISSN   0360-8352 . S2CID   257990456 .
  13. ^ Jump up to: а б М. Дориго, «Оптимизация, обучение и естественные алгоритмы» , докторская диссертация, Миланский политехнический университет, Италия, 1992.
  14. ^ Jump up to: а б Москато, П. (1989). «Об эволюции, поиске, оптимизации, генетических алгоритмах и боевых искусствах: на пути к меметическим алгоритмам» . Программа параллельных вычислений Калифорнийского технологического института (отчет 826).
  15. ^ Томойагэ Б., Чиндрис М., Сампер А., Судрия-Андреу А., Виллафафила-Роблес Р. Оптимальная по Парето реконфигурация систем распределения электроэнергии с использованием генетического алгоритма на основе NSGA-II. Энергии. 2013 г.; 6 (3): 1439–1455.
  16. ^ Ганесан, Т.; Эламвазути, И.; Ку Шаари, Ку Зилати; Васант, П. (01 марта 2013 г.). «Роевой интеллект и алгоритм гравитационного поиска для многокритериальной оптимизации производства синтез-газа». Прикладная энергетика . 103 : 368–374. Бибкод : 2013ApEn..103..368G . дои : 10.1016/j.apenergy.2012.09.059 .
  17. ^ Ганесан, Т.; Эламвазути, И.; Васант, П. (1 ноября 2011 г.). «Эволюционный метод пересечения нормальных границ (ENBI) для многокритериальной оптимизации системы формования зеленого песка». 2011 Международная конференция IEEE по системам управления, вычислениям и инженерии . стр. 86–91. doi : 10.1109/ICCSCE.2011.6190501 . ISBN  978-1-4577-1642-3 . S2CID   698459 .
  18. ^ Жарбуи, Бассем; Сиарри, Патрик; Тегем, Жак, ред. (2013). Метаэвристика для планирования производства . Серия «Автоматизация – управление и промышленное строительство». Лондон: ИСТЭ. ISBN  978-1-84821-497-2 .
  19. ^ Джафа, Фатос; Авраам, Аджит, ред. (2008). Метаэвристика для планирования в промышленных и производственных приложениях . Исследования в области вычислительного интеллекта. Том. 128. Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-540-78985-7 . ISBN  978-3-540-78984-0 . S2CID   42238720 .
  20. ^ Якоб, Вильфрид; Страк, Сильвия; Квинт, Александр; Бенгель, Гюнтер; Стаки, Карл-Уве; Зюсс, Вольфганг (22 апреля 2013 г.). «Быстрое перепланирование нескольких рабочих процессов для ограниченных гетерогенных ресурсов с использованием многокритериальных меметических вычислений» . Алгоритмы . 6 (2): 245–277. дои : 10.3390/a6020245 . ISSN   1999-4893 .
  21. ^ Кизилай, Дамла; Тасгетирен, М. Фатих; Пан, Куан-Ке; Зюер, Гюрсель (2019). «Ансамбль метаэвристик для задачи планирования энергоэффективного блокирующего цеха» . Производство Процедиа . 39 : 1177–1184. дои : 10.1016/j.promfg.2020.01.352 . S2CID   213710393 .
  22. ^ Грош, Бенедикт; Вайцель, Тимм; Пантен, Никлас; Абеле, Эберхард (2019). «Метаэвристика энергоадаптивного планирования производства с несколькими энергоносителями и ее реализация в реальной производственной системе» . Процесс CIRP . 80 : 203–208. doi : 10.1016/j.procir.2019.01.043 . S2CID   164850023 .
  23. ^ Jump up to: а б Холланд, Дж. Х. (1975). Адаптация в природных и искусственных системах . Издательство Мичиганского университета. ISBN  978-0-262-08213-6 .
  24. ^ Jump up to: а б Гловер, Фред (1977). «Эвристика целочисленного программирования с использованием суррогатных ограничений». Науки о принятии решений . 8 (1): 156–166. CiteSeerX   10.1.1.302.4071 . дои : 10.1111/j.1540-5915.1977.tb01074.x .
  25. ^ Jump up to: а б Гловер, Ф. (1986). «Будущие пути целочисленного программирования и связи с искусственным интеллектом». Компьютеры и исследования операций . 13 (5): 533–549. дои : 10.1016/0305-0548(86)90048-1 .
  26. ^ Гупта, Шубхам; Абдеразек, Хаммуди; Йылдыз, Бетюль Султан; Йылдыз, Али Риза; Мирджалили, Сейедали; Саит, Садик М. (2021). «Сравнение алгоритмов метаэвристической оптимизации для решения задач оптимизации механического проектирования с ограничениями» . Экспертные системы с приложениями . 183 : 115351. doi : 10.1016/j.eswa.2021.115351 .
  27. ^ Квинт, Александр; Якоб, Вильфрид; Шерер, Клаус-Петер; Эггерт, Хорст (2002), Лаудон, Мэтью (редактор), «Оптимизация пластины микропривода с использованием эволюционных алгоритмов и моделирования на основе методов дискретных элементов» , Международная конференция по моделированию и симуляции микросистем: MSM 2002 , Кембридж, Массачусетс: Вычислительные публикации, стр. 192–197, ISBN.  978-0-9708275-7-9
  28. ^ Парми, IC (1997), Дасгупта, Дипанкар; Михалевич, Збигнев (ред.), «Стратегии интеграции эволюционного/адаптивного поиска с процессом инженерного проектирования» , «Эволюционные алгоритмы в инженерных приложениях » , Берлин, Гейдельберг: Springer, стр. 453–477, doi : 10.1007/978-3 -662-03423-1_25 , ISBN  978-3-642-08282-5 , получено 17 июля 2023 г.
  29. ^ Валади, Джаяраман; Сиарри, Патрик, ред. (2014). Применение метаэвристики в технологическом проектировании . Чам: Международное издательство Springer. дои : 10.1007/978-3-319-06508-3 . ISBN  978-3-319-06507-6 . S2CID   40197553 .
  30. ^ Санчес, Эрнесто; Скиллеро, Джованни; Тонда, Альберто (2012). Промышленное применение эволюционных алгоритмов . Справочная библиотека интеллектуальных систем. Том. 34. Берлин, Гейдельберг: Шпрингер. дои : 10.1007/978-3-642-27467-1 . ISBN  978-3-642-27466-4 .
  31. ^ Акан, Таймаз; Антер, Ахмед М.; Этанер-Уяр, А. Шима; Олива, Диего, ред. (2023). Инженерные приложения современной метаэвристики . Исследования в области вычислительного интеллекта. Том. 1069. Чам: Springer International Publishing. дои : 10.1007/978-3-031-16832-1 . ISBN  978-3-031-16831-4 . S2CID   254222401 .
  32. ^ Блюм, Кристиан (2000), Каньони, Стефано (редактор), «Оптимизированное создание операторов перемещения робота без столкновений с помощью эволюционного программного обеспечения GLEAM» , Реальные приложения эволюционных вычислений , Конспекты лекций по информатике, том. 1803, Берлин, Гейдельберг: Springer, стр. 330–341, doi : 10.1007/3-540-45561-2_32 , ISBN.  978-3-540-67353-8 , получено 17 июля 2023 г.
  33. ^ Пхолди, Нантиват; Бурерат, Суджин (14 декабря 2018 г.), «Многокритериальное планирование траектории 6D-робота на основе многокритериального метаэвристического поиска» , Международная конференция по сетям, коммуникации и вычислениям (ICNCC 2018) , ACM, стр. 352–356, doi : 10.1145/3301326.3301356 , ISBN  978-1-4503-6553-6 , S2CID   77394395
  34. ^ Jump up to: а б Москато, П. (2012). «Метаэвристическая оптимизация лежит в основе исследования и сравнительного анализа». Мягкий компьютер . 16 (3): 527–561. дои : 10.1007/s00500-011-0754-8 . hdl : 11441/24597 . S2CID   1497912 .
  35. ^ Роббинс, Х.; Монро, С. (1951). «Метод стохастической аппроксимации» (PDF) . Анналы математической статистики . 22 (3): 400–407. дои : 10.1214/aoms/1177729586 .
  36. ^ Барричелли, Н. А. (1954). «Численные примеры эволюционных процессов». Методы : 45–68.
  37. ^ Растригин Л.А. (1963). «Сходимость метода случайного поиска в экстремальном управлении многопараметрической системой». Автоматизация и дистанционное управление . 24 (10): 1337–1342.
  38. ^ Матьяс, Дж. (1965). «Случайная оптимизация» . Автоматизация и дистанционное управление . 26 (2): 246–253.
  39. ^ Нелдер, Дж.А.; Мид, Р. (1965). «Симплексный метод минимизации функции». Компьютерный журнал . 7 (4): 308–313. дои : 10.1093/comjnl/7.4.308 . S2CID   2208295 .
  40. ^ Рехенберг, Инго (1965). «Кибернетический путь решения экспериментальной задачи». Королевское авиационное учреждение, библиотечный перевод .
  41. ^ Фогель, Л.; Оуэнс, Эй Джей; Уолш, MJ (1966). Искусственный интеллект посредством моделирования эволюции . Уайли. ISBN  978-0-471-26516-0 .
  42. ^ Гастингс, WK (1970). «Методы выборки Монте-Карло с использованием цепей Маркова и их приложения». Биометрика . 57 (1): 97–109. Бибкод : 1970Бимка..57...97H . дои : 10.1093/biomet/57.1.97 . S2CID   21204149 .
  43. ^ Кавиккио, диджей (1970). «Адаптивный поиск с использованием моделирования эволюции». Технический отчет . Мичиганский университет, факультет компьютерных и коммуникационных наук. hdl : 2027.42/4042 .
  44. ^ Керниган, BW; Лин, С. (1970). «Эффективная эвристическая процедура разделения графов». Технический журнал Bell System . 49 (2): 291–307. дои : 10.1002/j.1538-7305.1970.tb01770.x .
  45. ^ Мерсер, RE; Сэмпсон, младший (1978). «Адаптивный поиск с использованием репродуктивного метаплана». Кибернет . 7 (3): 215–228. дои : 10.1108/eb005486 .
  46. ^ Смит, С.Ф. (1980). Система обучения на основе генетических адаптивных алгоритмов (кандидатская диссертация). Университет Питтсбурга.
  47. ^ Киркпатрик, С.; Гелатт-младший, компакт-диск; Векки, член парламента (1983). «Оптимизация путем моделирования отжига». Наука . 220 (4598): 671–680. Бибкод : 1983Sci...220..671K . CiteSeerX   10.1.1.123.7607 . дои : 10.1126/science.220.4598.671 . ПМИД   17813860 . S2CID   205939 .
  48. ^ Москато, П.; Фонтанари, Дж. Ф. (1990), «Стохастическое и детерминистическое обновление при моделировании отжига», Physics Letters A , 146 (4): 204–208, Бибкод : 1990PhLA..146..204M , doi : 10.1016/0375-9601(90) 90166-Л
  49. ^ Дуек, Г.; Шойер, Т. (1990), «Принятие порога: алгоритм оптимизации общего назначения, превосходящий имитацию отжига», Journal of Computational Physics , 90 (1): 161–175, Bibcode : 1990JCoPh..90..161D , doi : 10.1016/0021-9991(90)90201-Б , ISSN   0021-9991
  50. ^ Вулперт, Д.Х.; Макреди, WG (1995). «Нет теорем бесплатного обеда для поиска». Технический отчет СФИ-ТР-95-02-010 . Институт Санта-Фе. S2CID   12890367 .
  51. ^ Игель, Кристиан, Туссен, Марк (июнь 2003 г.). «О классах функций, для которых не верны результаты бесплатного обеда». Письма об обработке информации . 86 (6): 317–321. arXiv : cs/0108011 . дои : 10.1016/S0020-0190(03)00222-9 . ISSN   0020-0190 . S2CID   147624 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  52. ^ Оже, Энн , Тейто, Оливье (2010). «Постоянные обеды бесплатны плюс разработка алгоритмов оптимальной оптимизации». Алгоритмика . 57 (1): 121–146. CiteSeerX   10.1.1.186.6007 . дои : 10.1007/s00453-008-9244-5 . ISSN   0178-4617 . S2CID   1989533 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  53. ^ Стефан Дросте; Томас Янсен; Инго Вегенер (2002). «Оптимизация с помощью эвристики рандомизированного поиска - теорема (A) НФЛ, реалистичные сценарии и сложные функции». Теоретическая информатика . 287 (1): 131–144. CiteSeerX   10.1.1.35.5850 . дои : 10.1016/s0304-3975(02)00094-4 .

Дальнейшее чтение

[ редактировать ]
[ редактировать ]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Metaheuristic&oldid=1228754175"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: b626c73ada8feac582b5d8fe516562df__1718228040
URL1:https://arc.ask3.ru/arc/aa/b6/df/b626c73ada8feac582b5d8fe516562df.html
Заголовок, (Title) документа по адресу, URL1:
Metaheuristic - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)