✖


Jump to content

Дискретное дипольное приближение

В приближении дискретных диполей более крупный объект аппроксимируется дискретными излучающими электрическими диполями.

Дискретное дипольное приближение ( DDA ), также известное как связанное дипольное приближение , [1] — метод расчета рассеяния излучения частицами произвольной формы и периодическими структурами. Учитывая цель произвольной геометрии, пытаются вычислить ее свойства рассеяния и поглощения путем аппроксимации непрерывной цели конечным набором небольших поляризуемых диполей . Этот метод используется в различных приложениях, включая нанофотонику , радиолокационное рассеяние, физику аэрозолей и астрофизику .



Величина напряженности электрического поля (цветной) и вектор Пойнтинга (черные стрелки) в ближнем поле вертикально ориентированного диполя в плоскости изображения. Синий/красный цвета обозначают электрическое поле, ориентированное вниз/вверх.

Основные понятия

[ редактировать ]

Основная идея DDA была предложена ДеВо в 1964 году. [2] кто применил его для изучения оптических свойств молекулярных агрегатов; эффекты замедления не были включены, поэтому лечение ДеВо ограничивалось агрегатами, которые были малы по сравнению с длиной волны. DDA, включая эффекты замедления, был предложен в 1973 году Перселлом и Пеннипакером. [3] который использовал его для изучения межзвездных пылевых частиц. Проще говоря, DDA представляет собой аппроксимацию непрерывной цели конечным набором поляризуемых точек. Точки приобретают дипольные моменты в ответ на локальное электрическое поле. Диполи взаимодействуют друг с другом через свои электрические поля, поэтому DDA также иногда называют приближением связанных диполей. [1] [4]

Природа послужила физическим источником вдохновения для DDA - Лоренц в 1909 году. [5] показал, что диэлектрические свойства вещества могут быть напрямую связаны с поляризуемостью отдельных атомов, из которых оно состоит, с особенно простым и точным соотношением Клаузиуса-Моссотти (или Лоренца-Лоренца), когда атомы расположены на кубической решетке. Мы можем ожидать, что точно так же, как континуальное представление твердого тела подходит для масштабов длины, больших по сравнению с межатомным расстоянием, массив поляризуемых точек может точно аппроксимировать реакцию непрерывной мишени на масштабах длины, больших по сравнению с междипольное разделение.

Для конечного массива точечных диполей проблема рассеяния может быть решена точно, поэтому единственное приближение, которое присутствует в DDA, - это замена непрерывной мишени массивом N-точечных диполей. Замена требует уточнения как геометрии (расположения диполей), так и поляризуемости диполей. Для монохроматических падающих волн может быть найдено самосогласованное решение для осциллирующих дипольных моментов; на основе них вычисляются сечения поглощения и рассеяния. Если решения МДА получены для двух независимых поляризаций падающей волны, то можно определить полную амплитудную матрицу рассеяния.Альтернативно, DDA может быть получено из объемного интегрального уравнения для электрического поля . [6] Это подчеркивает, что аппроксимация точечных диполей эквивалентна дискретизации интегрального уравнения и, таким образом, уменьшается с уменьшением размера диполя.

Признавая, что поляризуемости могут быть тензорами, DDA можно легко применить к анизотропным материалам. Распространение DDA на обработку материалов с ненулевой магнитной восприимчивостью также является простым, хотя для большинства применений магнитные эффекты незначительны.

Существует несколько обзоров метода DDA. [7] [6] [8] [9]

Метод был усовершенствован Дрэйном , Флатау и Гудманом, которые применили быстрое преобразование Фурье для решения задач быстрой свертки, возникающих в приближении дискретного диполя (DDA). Это позволило провести расчет рассеяния крупными целями. Они распространяли открытый исходный код DDSCAT. [7] [10] Сейчас существует несколько реализаций DDA, [6] расширение периодических целей, [11] и частицы, помещенные на плоскую подложку или рядом с ней. [12] [13] Также были опубликованы сравнения с точными методами. [14] Другие аспекты, такие как критерии достоверности приближения дискретного диполя, были опубликованы. [15] DDA также был расширен за счет использования прямоугольных или кубовидных диполей. [16] которые более эффективны для сильно сплюснутых или вытянутых частиц.

Быстрое преобразование Фурье для быстрых вычислений свертки

[ редактировать ]

Метод быстрого преобразования Фурье (БПФ) был представлен в 1991 году Гудманом, Дрэйном и Флатау. [17] для дискретного дипольного приближения. Они использовали 3D FFT GPFA, написанный Клайвом Темпертоном. Матрица взаимодействия была увеличена вдвое по сравнению с исходным размером, чтобы включить отрицательные задержки путем зеркального отражения и обращения матрицы взаимодействия. С тех пор было разработано несколько вариантов. Барроуз, Тейшейра и Конг [18] в 2001 году разработал код, который использует переупорядочение блоков, заполнение нулями и алгоритм реконструкции, требуя минимального использования памяти. Макдональд, Голден и Дженнингс [19] в 2009 году использовал 1D-код БПФ и расширил матрицу взаимодействия в направлениях x, y и z вычислений БПФ, предполагая экономию памяти благодаря этому подходу. Этот вариант также был реализован в коде MATLAB 2021 Шабанинежадом и Рамакришной. [20] . Другие методы ускорения сверток были предложены в общем контексте. [21] [22] наряду с более быстрыми оценками быстрых преобразований Фурье, возникающими в средствах решения задач DDA.

Схемы итераций сопряженного градиента и предварительная подготовка

[ редактировать ]

Некоторые из ранних расчетов вектора поляризации были основаны на прямая инверсия [3] и реализация метода сопряженных градиентов Петровича и Куо-Петравича. [23] Впоследствии были протестированы многие другие методы сопряженных градиентов. [24] Сообщалось также о достижениях в предварительной обусловленности линейных систем уравнений, возникающих в установке DDA. [25]

Приближение теплового дискретного диполя

[ редактировать ]

Приближение теплового дискретного диполя представляет собой расширение исходного DDA для моделирования теплопередачи в ближнем поле между трехмерными объектами произвольной формы. [26] [27]

Коды дискретной дипольной аппроксимации

[ редактировать ]

Большинство кодов применимо к неоднородным немагнитным частицам произвольной формы и системам частиц в свободном пространстве или однородной диэлектрической среде. Рассчитываемые величины обычно включают матрицы Мюллера , интегральные сечения (затухание, поглощение и рассеяние), внутренние поля и поля рассеяния с угловым разрешением (фазовая функция). Есть несколько опубликованных сравнений существующих кодов DDA. [14]

Универсальные коды DDA с открытым исходным кодом

[ редактировать ]

Эти коды обычно используют регулярные сетки (кубический или прямоугольный кубоид), метод сопряженных градиентов для решения больших систем линейных уравнений и БПФ-ускорение матрично-векторных произведений, которое использует теорему свертки. Сложность этого подхода почти линейна по количеству диполей как для времени, так и для памяти. [6]

Имя Авторы Ссылки Язык Обновлено Функции
ДДСКАТ Дрен и Флатау [7] Фортран 2019 (v.  7.3.3) Также может обрабатывать периодические частицы и эффективно рассчитывать ближние поля . Использует ускорение OpenMP .
DDscat.C++ Чоли [28] С++ 2017 (v.  7.3.1) Версия DDSCAT, переведенная на C++, с некоторыми дополнительными улучшениями.
АДДА Юркин, Хукстра и участники [29] [30] С 2020 (v.  1.4.0) Реализует быстрое и точное рассмотрение плоской подложки и позволяет использовать прямоугольные кубовидные вокселы для сильно сплюснутых или вытянутых частиц. Также можно рассчитать усиление эмиссии (скорости затухания) точечных излучателей. Расчет ближнего поля не очень эффективен. Использует распараллеливание интерфейса передачи сообщений (MPI) и может работать на графическом процессоре ( OpenCL ).
OpenDDA Макдональдс [19] [31] С 2009 (v.  0.4.1) Использует распараллеливание OpenMP и MPI. Основное внимание уделяется вычислительной эффективности.
ДДА-графический процессор Кисс [32] С++ 2016 Работает на графическом процессоре (OpenCL). Алгоритмы частично основаны на ADDA.
ВИЭ-БПФ Напиток [33] С/С++ 2019 Также рассчитывает ближние поля и поглощение материала. Назван по-другому, но алгоритмы очень похожи на те, которые используются в основном DDA.
VoxScatter Грот, Полимеридис и Уайт [34] Матлаб 2019 Использует циркулянтный предобуславливатель для ускорения итеративных решателей.
ЕСЛИ-DDA Шоме, Сентенак и Сентенак [35] Фортран, графический интерфейс на C++ с Qt 2021 (v.  0.9.19) Дружественный к идиотам DDA. Использует OpenMP и HDF5. Имеет отдельную версию (IF-DDAM) для многослойной подложки.
МПДДА Шабанинежад, Аван и Рамакришна [20] Матлаб 2021 (v.  1.0) Работает на графическом процессоре (с использованием возможностей Matlab)

Специализированные коды DDA

[ редактировать ]

В этот список входят коды, которые не подпадают под предыдущий раздел. Причины могут быть следующими: исходный код недоступен, ускорение БПФ отсутствует или уменьшено, код ориентирован на конкретные приложения, что не позволяет легко вычислить стандартные величины рассеяния.


Имя Авторы Ссылки Язык Обновлено Функции
DDSURF, DDSUB, DDFILM Шмель, Небекер и Чжан [12] [36] [37] Фортран 2008 Строгая обработка полубесконечной подложки и конечных пленок (с произвольным размещением частиц), но БПФ используется только 2D-ускорение .
ДДММ Маковский [38] Фортран 2002 Вычисляет T-матрицу , которую затем можно использовать для эффективного расчета свойств рассеяния, усредненных по ориентации.
CDA МакМахон [39] Матлаб 2006
ДДА-СИ Выше [40] Матлаб 2014 (v.  0.2) Строгая обработка подложки без использования ускорения БПФ.
ПИДДА Dmitriev Питон 2015 Повторная реализация DDA-SI
е -DDA Василло и Бигелоу [41] Фортран 2019 (v.  2.0) Имитирует спектроскопию потерь энергии электронов и катодолюминесценцию. Построен на базе DDSCAT 7.1.
ДДЕЭЛС Геке, Гийом и Анрар [42] Фортран 2013 (v.  2.1) Имитирует спектроскопию потерь энергии электронов и катодолюминесценцию. Обрабатывает подложку посредством аппроксимации изображения, но ускорение БПФ не используется.
Т-ДДА Эдалатпур [43] Фортран 2015 Имитирует радиационную теплопередачу в ближнем поле. Узким местом вычислений является прямая инверсия матрицы (ускорение БПФ не используется). Использует распараллеливание OpenMP и MPI.
CDDA Розалес, Альбелла, Гонсалес, Гутьеррес и Морено [44] 2021 Применяется к киральным системам (решает связанные уравнения для электрических и магнитных полей).
PyDScat Ибинь Цзян, Абхишек Шарма и Лерой Кронин [45] Питон 2023 Имитирует наноструктуры, претерпевающие структурную трансформацию с ускорением графического процессора.
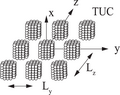
[ редактировать ]
  • Рассеяние на периодических структурах, таких как пластины, решетки, периодические кубы, расположенные на поверхности, можно решить в приближении дискретного диполя.
    Рассеяние на периодических структурах, таких как пластины, решетки, периодические кубы, расположенные на поверхности, можно решить в приближении дискретного диполя.
  • Рассеяние бесконечным объектом (например, цилиндром) можно решить в приближении дискретного диполя.
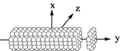
    Рассеяние бесконечным объектом (например, цилиндром) можно решить в приближении дискретного диполя.

См. также

[ редактировать ]

Ссылки

[ редактировать ]
  1. ^ Перейти обратно: а б Сингхэм, Шермила Б.; Зальцман, Гэри К. (1986). «Оценка матрицы рассеяния произвольной частицы с использованием приближения связанного диполя». Дж. Хим. Физ . 84 (5). Издательство АИП: 2658–2667. Бибкод : 1986ЖЧФ..84.2658С . дои : 10.1063/1.450338 .
  2. ^ ДеВо, Ховард (15 июля 1964 г.). «Оптические свойства молекулярных агрегатов. I. Классическая модель электронного поглощения и преломления». Дж. Хим. Физ . 41 (2). Издательство AIP: 393–400. Бибкод : 1964ЖЧФ..41..393Д . дои : 10.1063/1.1725879 .
  3. ^ Перейти обратно: а б Э. М. Перселл; Ч. Р. Пеннипакер (1973). «Рассеяние и поглощение света несферическими диэлектрическими зернами». Астрофиз. Дж . 186 : 705. Бибкод : 1973ApJ...186..705P . дои : 10.1086/152538 .
  4. ^ Сингхэм, Шермила Брито; Борен, Крейг Ф. (1 января 1987 г.). «Рассеяние света произвольной частицей: физическая переформулировка метода связанных диполей». Опция Летт . 12 (1). Оптическое общество: 10–12. Бибкод : 1987OptL...12...10S . дои : 10.1364/ол.12.000010 . ПМИД   19738776 .
  5. ^ Х. А. Лоренц, Теория электронов (Тойбнер, Лейпциг, 1909)
  6. ^ Перейти обратно: а б с д М.А. Юркин; А.Г. Хоекстра (2007). «Приближение дискретного диполя: обзор и последние разработки» (PDF) . Дж. Квант. Спектроск. Радиат. Передача . 106 (1–3): 558–589. arXiv : 0704.0038 . Бибкод : 2007JQSRT.106..558Y . дои : 10.1016/j.jqsrt.2007.01.034 . S2CID   119572857 .
  7. ^ Перейти обратно: а б с Дрен, Британская Колумбия; П. Дж. Флатау (1994). «Дискретное дипольное приближение для расчетов рассеяния». J. Опт. Соц. Являюсь. А. ​ 11 (4): 1491–1499. Бибкод : 1994JOSAA..11.1491D . дои : 10.1364/JOSAA.11.001491 .
  8. ^ Юркин, Максим А. (2023). «Дискретное дипольное приближение». Свет, плазмоника и частицы . Эльзевир. стр. 167–198.
  9. ^ Шоме, Патрик Кристиан (2022). «Дискретное дипольное приближение: обзор» . Математика . 10 (17). MDPI: 3049. doi : 10.3390/math10173049 .
  10. ^ БТ Дренаж; П. Дж. Флатау (2008). «Дискретное дипольное приближение для периодических целей: теория и испытания». J. Опт. Соц. Являюсь. А. ​ 25 (11): 2693–3303. arXiv : 0809.0338 . Бибкод : 2008JOSAA..25.2693D . дои : 10.1364/JOSAA.25.002693 . ПМИД   18978846 . S2CID   15747060 .
  11. ^ Шоме, Патрик С.; Рахмани, Адель; Брайант, Гарнетт В. (2 апреля 2003 г.). «Обобщение метода связанных диполей на периодические структуры». Физ. Преподобный Б. 67 (16). Американское физическое общество (APS): 165404. arXiv : Physics/0305051 . Бибкод : 2003PhRvB..67p5404C . дои : 10.1103/physrevb.67.165404 . S2CID   26726283 .
  12. ^ Перейти обратно: а б Шмель, Роланд; Небекер, Брент М.; Хирлеман, Э. Дэн (1 ноября 1997 г.). «Дискретно-дипольное приближение для рассеяния на деталях на поверхностях с помощью двумерного метода быстрого преобразования Фурье». J. Опт. Соц. Являюсь. А. ​ 14 (11). Оптическое общество: 3026–3036. Бибкод : 1997JOSAA..14.3026S . дои : 10.1364/josaa.14.003026 .
  13. ^ М.А. Юркин; М. Хунтеманн (2015). «Строгое и быстрое дискретное дипольное приближение для частиц вблизи плоской границы раздела» (PDF) . Журнал физической химии C. 119 (52): 29088–29094. дои : 10.1021/acs.jpcc.5b09271 .
  14. ^ Перейти обратно: а б Пенттиля, Антти; Зубко, Евгений; Люмме, Кари; Муйнонен, Карри; Юркин Максим А.; и др. (2007). «Сравнение реализаций дискретного диполя и точных методов». Дж. Квант. Спектроск. Радиат. Передача . 106 (1–3). Эльзевир Б.В.: 417–436. Бибкод : 2007JQSRT.106..417P . дои : 10.1016/j.jqsrt.2007.01.026 .
  15. ^ Зубко, Евгений; Петров Дмитрий; Гринко Евгений; Шкуратов Юрий; Окамото, Хадзиме; и др. (04 марта 2010 г.). «Критерии достоверности дискретного дипольного приближения». Прил. Опц . 49 (8). Оптическое общество: 1267–1279. Бибкод : 2010ApOpt..49.1267Z . дои : 10.1364/ao.49.001267 . hdl : 2115/50065 . ПМИД   20220882 .
  16. ^ Д.А. Смунев; ПК Шоме; М.А. Юркин (2015). «Прямоугольные диполи в приближении дискретных диполей» (PDF) . Дж. Квант. Спектроск. Радиат. Передача . 156 : 67–79. Бибкод : 2015JQSRT.156...67S . дои : 10.1016/j.jqsrt.2015.01.019 .
  17. ^ Гудман, Джон Дж.; Дрен, Брюс Т.; Флатау, Петр Дж. (1991). «Применение методов быстрого преобразования Фурье к приближению дискретного диполя». Оптические письма . 16 (15). Издательская группа «Оптика»: 1198–1200. дои : 10.1364/OL.16.001198 .
  18. ^ Бэрроуз, Бельгия; Тейшейра, Флорида; Конг, JA (2001). «Быстрый алгоритм матрично-векторного умножения асимметричных многоуровневых блочных теплицевых матриц в трехмерном рассеянии». Письма о микроволновых и оптических технологиях . 31 (1): 28–32. дои : 10.1002/mop.1348 .
  19. ^ Перейти обратно: а б Дж. Макдональд; А. Золотой; Дж. Дженнингс (2009). «OpenDDA: новая высокопроизводительная вычислительная среда для дискретного дипольного приближения». Межд. J. Высокая производительность. Комп. Приложение . 23 (1): 42–61. arXiv : 0908.0863 . Бибкод : 2009arXiv0908.0863M . дои : 10.1177/1094342008097914 . S2CID   10285783 .
  20. ^ Перейти обратно: а б М. Шабанинежад; М.Г. Аван; Г. Рамакришна (2021). «Пакет MATLAB для дискретной дипольной аппроксимации с помощью графического процессора: быстрое преобразование Фурье и бисопряженный градиент». Дж. Квант. Спектроск. Радиат. Передача . 262 : 107501. Бибкод : 2021JQSRT.26207501S . дои : 10.1016/j.jqsrt.2020.107501 . S2CID   233839571 .
  21. ^ Фу, Дэниел Ю; Кумбонг, Герман; Нгуен, Эрик; Ре, Кристофер (2023). «FlashFFTConv: эффективные свертки для длинных последовательностей с тензорными ядрами». arXiv : 2311.05908 [ cs.LG ].
  22. ^ Боуман, Джон К.; Робертс, Малькольм (2011). «Эффективные обработанные свертки без заполнения». Журнал SIAM по научным вычислениям . 33 (1). СИАМ: 386–406. arXiv : 1008.1366 . Бибкод : 2011ГАО...33..386Б . дои : 10.1137/100787933 .
  23. ^ Петрович, М.; Куо-Петравич, Г. (1979). «Алгоритм ILUCG, минимизирующий евклидову норму» . Журнал вычислительной физики . 32 (2): 263–269. дои : 10.1016/0021-9991(79)90133-5 .
  24. ^ Шоме, Патрик К. (2024). «Сравнительное исследование эффективных итерационных решателей дискретного дипольного приближения». Журнал количественной спектроскопии и переноса излучения . 312 . Эльзевир. Бибкод : 2024JQSRT.31208816C . дои : 10.1016/j.jqsrt.2023.108816 . S2CID   264805146 .
  25. ^ Шоме, Патрик С.; Мэр, Гийом; Сентенак, Энн (2023). «Ускорение дискретного дипольного приближения путем инициализации скалярным решением и использования циркулянтной предварительной обработки». Журнал количественной спектроскопии и переноса излучения . 298 . Эльзевир. Бибкод : 2023JQSRT.29808505C . дои : 10.1016/j.jqsrt.2023.108505 .
  26. ^ Эдалатпур, С.; Чума, М.; Труакс, Т.; Бэкман, Р.; Франкёр, М. (2015). «Анализ сходимости приближения теплового дискретного диполя». Физический обзор E . 91 (6): 063307. arXiv : 1502.02186 . дои : 10.1103/PhysRevE.91.063307 .
  27. ^ Монкада-Вилла, Э.; Куэвас, JC (2022). «Тепловое дискретное дипольное приближение для радиационной теплопередачи в ближнем поле в системах многих тел с произвольными невзаимными телами». Физический обзор B . 106 (23): 235430. arXiv : 2206.14921 . дои : 10.1103/PhysRevB.106.235430 .
  28. ^ В.Ю. Чолий (2013). «Программа дискретной дипольной аппроксимации DDscat.C++: особенности, ограничения и планы» . Адв. Астрон. Космическая физика . 3 : 66–70. Бибкод : 2013AASP....3...66C .
  29. ^ М.А. Юркин; В.П. Мальцев; А.Г. Хоекстра (2007). «Приближение дискретного диполя для моделирования рассеяния света частицами, размер которых намного превышает длину волны» (PDF) . Дж. Квант. Спектроск. Радиат. Передача . 106 (1–3): 546–557. arXiv : 0704.0037 . Бибкод : 2007JQSRT.106..546Y . дои : 10.1016/j.jqsrt.2007.01.033 . S2CID   119574693 .
  30. ^ М.А. Юркин; А.Г. Хоекстра (2011). «Код дискретно-дипольного приближения ADDA: возможности и известные ограничения» (PDF) . Дж. Квант. Спектроск. Радиат. Передача . 112 (13): 2234–2247. Бибкод : 2011JQSRT.112.2234Y . дои : 10.1016/j.jqsrt.2011.01.031 .
  31. ^ Дж. Макдональд (2007). OpenDDA - новая высокопроизводительная вычислительная среда для дискретного дипольного приближения (PDF) (доктор философии). Голуэй: Национальный университет Ирландии.
  32. ^ М. Циммерманн; А. Таусендфройнд; С. Патцельт; Г. Гох; С. Кисс; М.З. Шейх; М. Грегуар; С. Саймон (2012). «Процедура измерения структур размером менее 100 нм» . J. Лазерное приложение . 24 (4): 042010. Бибкод : 2012JLasA..24d2010Z . дои : 10.2351/1.4719936 .
  33. ^ ВЭЙ Ша; ЧМ Чой; Ю. П. Чен; У. К. Чу (2011). «Оптическая схема органического солнечного элемента с гибридной плазмонной системой» . Опция Выражать . 19 (17): 15908–15918. Бибкод : 2011OExpr..1915908S . дои : 10.1364/OE.19.015908 . ПМИД   21934954 .
  34. ^ С. П. Грот; АГ Полимеридис; Дж. К. Уайт (2020). «Ускорение дискретного дипольного приближения посредством предварительной подготовки циркулянта». Дж. Квант. Спектроск. Радиат. Передача . 240 : 106689. Бибкод : 2020JQSRT.24006689G . дои : 10.1016/j.jqsrt.2019.106689 . S2CID   209969404 .
  35. ^ ПК Шоме; Д. Сентенак; Г. Мэр; Т. Чжан; А. Сентенак (2021). «IFDDA, простой в использовании код для моделирования поля, рассеянного трехмерными неоднородными объектами в стратифицированной среде: учебное пособие» . J. Опт. Соц. Являюсь. А. ​ 38 (12): 1841–1852. Бибкод : 2021JOSAA..38.1841C . дои : 10.1364/JOSAA.432685 .
  36. ^ Б.М. Небекер (1998). Моделирование рассеяния света от объектов над и под поверхностями с использованием приближения дискретного диполя (доктор философии). Темпе, Аризона, США: Университет штата Аризона.
  37. ^ Э. Бэй; Х. Чжан; ЭД Хирлеман (2008). «Применение дискретного дипольного приближения для диполей, встроенных в пленку». J. Опт. Соц. Являюсь. А. ​ 25 (7): 1728–1736. Бибкод : 2008JOSAA..25.1728B . дои : 10.1364/JOSAA.25.001728 . ПМИД   18594631 .
  38. ^ Д.В. Маковски (2002). «Метод дискретного дипольного момента для расчета Т-матрицы несферических частиц». J. Опт. Соц. Являюсь. А. ​ 19 (5): 881–893. Бибкод : 2002JOSAA..19..881M . дои : 10.1364/JOSAA.19.000881 . ПМИД   11999964 .
  39. ^ Доктор медицины МакМахон (2006). Влияние геометрического порядка на линейные и нелинейные оптические свойства металлических наночастиц (PDF) (доктор философии). Нэшвилл, Теннесси, США: Университет Вандербильта.
  40. ^ ВЛИ Локе; Премьер-министр Менгуч; Тимо А. Ниеминен (2011). «Приближение дискретного диполя с поверхностным взаимодействием: набор вычислительных инструментов для MATLAB». Дж. Квант. Спектроск. Радиат. Передача . 112 (11): 1711–1725. Бибкод : 2011JQSRT.112.1711L . дои : 10.1016/j.jqsrt.2011.03.012 .
  41. ^ Северо-Запад Бигелоу; А. Васчилло; В. Ибери; Дж. П. Камден; Диджей Масиелло (2012). «Характеристика электронных и фотонных плазмонных возбуждений металлических наностержней». АСУ Нано . 6 (8): 7497–7504. дои : 10.1021/nn302980u . ПМИД   22849410 .
  42. ^ Н. Геке; Л. Хенрард (2010). «EELS и оптический отклик наночастицы благородного металла в рамках дискретного дипольного приближения». Ультрамикроскопия . 110 (8): 1075–1080. дои : 10.1016/j.ultramic.2010.01.013 .
  43. ^ С. Эдалатпур; М. Чума; Т. Труакс; Р. Бэкман; М. Франкёр (2015). «Анализ сходимости приближения теплового дискретного диполя». Физ. Преподобный Е. 91 (6): 063307. arXiv : 1502.02186 . Бибкод : 2015PhRvE..91f3307E . дои : 10.1103/PhysRevE.91.063307 . ПМИД   26172822 . S2CID   21556373 .
  44. ^ С.А. Росалес; П. Альбелла; Ф. Гонсалес; Ю. Гутьеррес; Ф. Морено (2021). «CDDA: расширение и анализ дискретного дипольного приближения для киральных систем» . Опция Выражать . 29 (19): 30020–30034. Бибкод : 2021OExpr..2930020R . дои : 10.1364/OE.434061 . hdl : 10902/24774 . ПМИД   34614734 .
  45. ^ Цзян, Ибинь; Шарма, Абхишек; Кронин, Лерой (2023). «Ускоренный метод исследования спектральных свойств динамически развивающихся наноструктур» . Журнал физической химии . 14 (16): 3929–3938. doi : 10.1021/acs.jpclett.3c00395 . ПМЦ   10150391 . ПМИД   37078273 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Discrete_dipole_approximation&oldid=1237305233#Discrete_dipole_approximation_codes"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: c5f391ed761bc50f3073df2e19683e84__1722213300
URL1:https://arc.ask3.ru/arc/aa/c5/84/c5f391ed761bc50f3073df2e19683e84.html
Заголовок, (Title) документа по адресу, URL1:
Discrete dipole approximation - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)