Бинарное дерево поиска

Бинарное дерево поиска
Бинарное дерево поиска
Тип	дерево
Изобретенный	1960
Изобретён	П.Ф. Уиндли, А.Д. Бут , Эй.Дж.Т. Колин и Т.Н. Хиббард
Операция
Временная сложность в обозначении большого О
Операция	Средний
Поиск	О( вход )
Вставлять	О( вход )
Удалить	О( вход )
Пространственная сложность
Космос	На )

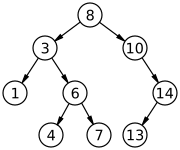
В информатике двоичное дерево поиска ( BST ), также называемое упорядоченным или отсортированным двоичным деревом , представляет собой корневую двоичного дерева структуру данных , в которой ключ каждого внутреннего узла больше, чем все ключи в левом поддереве соответствующего узла, и меньше, чем все ключи в левом поддереве соответствующего узла. те, что находятся в его правом поддереве. Временная сложность операций над бинарным деревом поиска линейна относительно высоты дерева.

Деревья двоичного поиска позволяют осуществлять двоичный поиск для быстрого поиска, добавления и удаления элементов данных. Поскольку узлы в BST расположены так, что каждое сравнение пропускает около половины оставшегося дерева, производительность поиска пропорциональна производительности двоичного логарифма . BST были разработаны в 1960-х годах для решения проблемы эффективного хранения размеченных данных и приписываются Конвею Бернерсу-Ли и Дэвиду Уиллеру .

Производительность двоичного дерева поиска зависит от порядка вставки узлов в дерево, поскольку произвольные вставки могут привести к вырождению; можно построить несколько вариантов двоичного дерева поиска с гарантированной производительностью в худшем случае. К основным операциям относятся: поиск, обход, вставка и удаление. BST с гарантированной сложностью наихудшего случая работают лучше, чем несортированный массив, для которого потребуется линейное время поиска .

Анализ сложности BST показывает, что в среднем вставка, удаление и поиск занимают $O(\log n)$ для $n$ узлы. В худшем случае они деградируют до односвязного списка: $O(n)$ . Чтобы решить проблему безграничного увеличения высоты дерева с помощью произвольных вставок и удалений, самобалансирующиеся вводятся варианты BST, которые связывают наихудшую сложность поиска со сложностью двоичного логарифма. Деревья AVL были первыми самобалансирующими двоичными деревьями поиска, изобретенными в 1962 году Георгием Адельсоном-Вельским и Евгением Ландисом .

Двоичные деревья поиска могут использоваться для реализации абстрактных типов данных, таких как динамические наборы , таблицы поиска и очереди приоритетов , а также использоваться в алгоритмах сортировки, таких как сортировка по дереву .

История

Алгоритм бинарного дерева поиска был открыт независимо несколькими исследователями, в том числе П. Ф. Уиндли, Эндрю Дональдом Бутом , Эндрю Колином , Томасом Н. Хиббардом . ^{[ 1 ]}^{[ 2 ]} Алгоритм приписывается Конвею Бернерсу-Ли и Дэвиду Уилеру , которые использовали его для хранения помеченных данных на магнитных лентах в 1960 году. ^{[ 3 ]} Одним из самых ранних и популярных алгоритмов двоичного дерева поиска является алгоритм Хиббарда. ^{[ 1 ]}

Временная сложность двоичного дерева поиска неограниченно увеличивается с высотой дерева, если узлы вставлены в произвольном порядке, поэтому были введены самобалансирующиеся деревья двоичного поиска, чтобы ограничить высоту дерева до $O(\log n)$ . ^{[ 4 ]} различные сбалансированные по высоте Для ограничения высоты дерева были введены бинарные деревья поиска, такие как деревья AVL , Treaps и красно-черные деревья . ^{[ 5 ]}

Дерево AVL было изобретено Георгием Адельсоном-Вельским и Евгением Ландисом в 1962 году для эффективной организации информации. ^{[ 6 ]}^{[ 7 ]} Это было первое самобалансирующееся двоичное дерево поиска. ^{[ 8 ]}

Обзор

Бинарное дерево поиска — это корневое двоичное дерево, в котором узлы расположены в строгом общем порядке , в котором узлы с ключами, большими, чем любой конкретный узел A, хранятся в правых поддеревьях по отношению к этому узлу A , а узлы с ключами, равными или меньше, чем A, хранятся в левых поддеревьях от A, удовлетворяя свойству двоичного поиска . ^{[ 9 ]}^: 298^{[ 10 ]}^: 287

Двоичные деревья поиска также эффективны при сортировке и алгоритмах поиска . Однако сложность поиска BST зависит от порядка, в котором узлы вставляются и удаляются; поскольку в худшем случае последовательные операции в двоичном дереве поиска могут привести к вырождению и формированию структуры, подобной односвязному списку (или «несбалансированному дереву»), поэтому в наихудшем случае он имеет ту же сложность, что и связанный список . ^{[ 11 ]}^{[ 9 ]}^: 299-302

Двоичные деревья поиска также являются фундаментальной структурой данных, используемой при построении абстрактных структур данных, таких как множества, мультимножества и ассоциативные массивы .

Операции

Идет поиск

Поиск в бинарном дереве поиска по определенному ключу можно запрограммировать рекурсивно или итеративно .

Поиск начинается с изучения корневого узла . Если дерево равно $nil$ , искомый ключ не существует в дереве. В противном случае, если ключ равен ключу корня, поиск успешен и узел возвращается. Если ключ меньше, чем у корня, поиск продолжается путем проверки левого поддерева. Аналогично, если ключ больше, чем ключ корня, поиск продолжается путем проверки правого поддерева. Этот процесс повторяется до тех пор, пока не будет найден ключ или пока не будет найдено оставшееся поддерево. ${\text{nil}}$ . Если искомый ключ не найден после ${\text{nil}}$ поддерево достигнуто, то ключ отсутствует в дереве. ^{[ 10 ]}^{: 290–291}

Рекурсивный поиск

Следующий псевдокод реализует процедуру поиска BST посредством рекурсии . ^{[ 10 ]}^: 290

Recursive-Tree-Search(x, key)
    if x = NIL or key = x.key then
        return x
    if key < x.key then
        return Recursive-Tree-Search(x.left, key)
    else
        return Recursive-Tree-Search(x.right, key)
    end if

Рекурсивная процедура продолжается до тех пор, пока ${\text{nil}}$ или ${\text{key}}$ встречаются искомые.

Итеративный поиск

Рекурсивную версию поиска можно «развернуть» в цикл while . На большинстве машин итеративная версия оказывается более эффективной . ^{[ 10 ]}^: 291

Iterative-Tree-Search(x, key)
    while x ≠ NIL and key ≠ x.key do
        if key < x.key then
            x := x.left
        else
            x := x.right
        end if
    repeat
    return x

Поскольку поиск может продолжаться до некоторого листового узла , сложность времени выполнения поиска BST равна $O(h)$ где $h$ это высота дерева . Однако худшим случаем для поиска BST является $O(n)$ где $n$ — общее количество узлов в BST, поскольку несбалансированный BST может выродиться в связанный список. Однако, если BST сбалансирован по высоте, высота будет $O(\log n)$ . ^{[ 10 ]}^: 290

Преемник и предшественник

Для определенных операций задан узел ${\text{x}}$ , нахождение преемника или предшественника ${\text{x}}$ имеет решающее значение. Предполагая, что все ключи BST различны, преемник узла ${\text{x}}$ в BST — это узел с наименьшим ключом, превышающим ${\text{x}}$ ключ. С другой стороны, предшественник узла ${\text{x}}$ в BST — это узел с наибольшим ключом, меньшим, чем ${\text{x}}$ ключ. Следующий псевдокод находит преемника и предшественника узла. ${\text{x}}$ в БСТ. ^{[ 12 ]}^{[ 13 ]}^{[ 10 ]}^{: 292–293}

 BST-Successor(x)
     if x.right ≠ NIL then
         return BST-Minimum(x.right)
     end if
     y := x.parent
     while y ≠ NIL and x = y.right do
         x := y
         y := y.parent
     repeat
     return y

 BST-Predecessor(x)
     if x.left ≠ NIL then
         return BST-Maximum(x.left)
     end if
     y := x.parent
     while y ≠ NIL and x = y.left do
         x := y
         y := y.parent
     repeat
     return y

Такие операции, как поиск узла в BST, ключ которого является максимальным или минимальным, имеют решающее значение в определенных операциях, таких как определение преемника и предшественника узлов. Ниже приведен псевдокод операций. ^{[ 10 ]}^{: 291–292}

 BST-Maximum(x)
     while x.right ≠ NIL do
         x := x.right
     repeat
     return x

 BST-Minimum(x)
     while x.left ≠ NIL do
         x := x.left
     repeat
     return x

Вставка

Такие операции, как вставка и удаление, приводят к динамическому изменению представления BST. Структура данных должна быть изменена таким образом, чтобы свойства BST сохранялись. Новые узлы вставляются как конечные узлы в BST. ^{[ 10 ]}^{: 294–295} Ниже приведена итеративная реализация операции вставки. ^{[ 10 ]}^: 294

1    BST-Insert(T, z)
2      y := NIL
3      x := T.root
4      while x ≠ NIL do
5        y := x
6        if z.key < x.key then
7          x := x.left
8        else
9          x := x.right
10       end if
11     repeat
12     z.parent := y
13     if y = NIL then
14       T.root := z
15     else if z.key < y.key then
16       y.left := z
17     else
18       y.right := z
19     end if

Процедура поддерживает «конечный указатель» ${\text{y}}$ как родитель ${\text{x}}$ . После инициализации в строке 2 цикл while в строках 4–11 вызывает обновление указателей. Если ${\text{y}}$ является ${\text{nil}}$ , BST пуст, поэтому ${\text{z}}$ вставляется как корневой узел двоичного дерева поиска ${\text{T}}$ , если это не так ${\text{nil}}$ , вставка продолжается путем сравнения ключей с ключами ${\text{y}}$ в строках 15-19 и узел вставляется соответственно. ^{[ 10 ]}^: 295

Удаление

Удаление узла, скажем ${\text{Z}}$ , из двоичного дерева поиска ${\text{BST}}$ имеет три случая: ^{[ 10 ]}^: 295-297

Если ${\text{Z}}$ является конечным узлом, родительским узлом ${\text{Z}}$ заменяется на ${\text{NIL}}$ и, следовательно, ${\text{Z}}$ удаляется из ${\text{BST}}$ , как показано в (а).
Если ${\text{Z}}$ имеет только одного дочернего узла, дочерний узел ${\text{Z}}$ получает повышение путем изменения родительского узла ${\text{Z}}$ чтобы указать на дочерний узел, следовательно, принимая ${\text{Z}}$ положение в дереве, как показано на рисунках (b) и (c).
Если ${\text{Z}}$ ${\text{Z}}$ имеет как левых, так и правых детей, наследник ${\text{Z}}$ ${\text{Z}}$ , сказать ${\text{Y}}$ ${\text{Y}}$ , вытесняет ${\text{Z}}$ ${\text{Z}}$ следуя двум случаям:
1. Если ${\text{Y}}$ является ${\text{Z}}$ правый дочерний элемент, как показано на (d), ${\text{Y}}$ вытесняет ${\text{Z}}$ и ${\text{Y}}$ Право ребенка остаются неизменными.
2. Если ${\text{Y}}$ лежит внутри ${\text{Z}}$ правое поддерево, но это не так ${\text{Z}}$ правый дочерний элемент, как показано на (e), ${\text{Y}}$ сначала заменяется своим собственным потомком, а затем вытесняет ${\text{Z}}$ позиция в дереве.

Следующий псевдокод реализует операцию удаления в двоичном дереве поиска. ^{[ 10 ]}^: 296-298

1    BST-Delete(BST, D)
2      if D.left = NIL then
3        Shift-Nodes(BST, D, D.right)
4      else if D.right = NIL then
5        Shift-Nodes(BST, D, D.left)
6      else
7        E := BST-Successor(D)
8        if E.parent ≠ D then
9          Shift-Nodes(BST, E, E.right)
10         E.right := D.right
11         E.right.parent := E
12       end if
13       Shift-Nodes(BST, D, E)
14       E.left := D.left
15       E.left.parent := E
16     end if

1    Shift-Nodes(BST, u, v)
2      if u.parent = NIL then
3        BST.root := v
4      else if u = u.parent.left then
5        u.parent.left := v
5      else
6        u.parent.right := v
7      end if
8      if v ≠ NIL then
9        v.parent := u.parent
10     end if

The ${\text{BST-Delete}}$ Процедура касается трех особых случаев, упомянутых выше. Строки 2–3 относятся к случаю 1; строки 4–5 относятся к случаю 2, а строки 6–16 — к случаю 3. Вспомогательная функция ${\text{Shift-Nodes}}$ используется в алгоритме удаления с целью замены узла ${\text{u}}$ с ${\text{v}}$ в бинарном дереве поиска ${\text{BST}}$ . ^{[ 10 ]}^: 298 Эта процедура обрабатывает удаление (и замену) ${\text{u}}$ от ${\text{BST}}$ .

Обход

BST может быть пройден с помощью трех основных алгоритмов: обход дерева в порядке , предзаказ и обход дерева в последующем порядке . ^{[ 10 ]}^: 287

Обход дерева по порядку : сначала посещаются узлы левого поддерева, затем корневой узел и правое поддерево. Такой обход посещает все узлы в порядке неубывающей последовательности ключей.
Обход дерева по предварительному заказу : сначала посещается корневой узел, а затем левое и правое поддеревья.
Обход дерева в постпорядке : сначала посещаются узлы левого поддерева, затем правое поддерево и, наконец, корень.

Ниже приведена рекурсивная реализация обхода дерева. ^{[ 10 ]}^{: 287–289}

 Inorder-Tree-Walk(x)
   if x ≠ NIL then
     Inorder-Tree-Walk(x.left)
     visit node
     Inorder-Tree-Walk(x.right)
   end if

 Preorder-Tree-Walk(x)
   if x ≠ NIL then
     visit node
     Preorder-Tree-Walk(x.left)
     Preorder-Tree-Walk(x.right)
   end if

 Postorder-Tree-Walk(x)
   if x ≠ NIL then
     Postorder-Tree-Walk(x.left)
     Postorder-Tree-Walk(x.right)
     visit node
   end if

Сбалансированные деревья двоичного поиска

Без перебалансировки вставки или удаления в двоичном дереве поиска могут привести к вырождению, что приведет к увеличению высоты. $n$ дерева (где $n$ — количество элементов в дереве), так что производительность поиска снижается до уровня линейного поиска. ^{[ 14 ]} Сохранение сбалансированности дерева поиска и ограничения высоты $O(\log n)$ является ключом к полезности двоичного дерева поиска. Этого можно достичь с помощью механизмов «самобалансировки» во время операций обновления дерева, предназначенных для поддержания высоты дерева на уровне двоично-логарифмической сложности. ^{[ 4 ]}^{[ 15 ]}^: 50

Деревья со сбалансированной высотой

Дерево является сбалансированным по высоте, если высоты левого и правого поддерева гарантированно связаны постоянным коэффициентом. Это свойство было введено деревом AVL и продолжено красно-черным деревом . ^{[ 15 ]}^: 50–51 Высоты всех узлов на пути от корня до измененного листового узла необходимо наблюдать и, возможно, корректировать при каждой операции вставки и удаления в дереве. ^{[ 15 ]}^: 52

Деревья со сбалансированным весом

В дереве со сбалансированным весом критерием сбалансированного дерева является количество листьев поддеревьев. Веса левого и правого поддеревьев отличаются не более чем на $1$ . ^{[ 16 ]}^{[ 15 ]}^: 61 Однако разница ограничена соотношением $\alpha$ гирь, поскольку условие сильного баланса $1$ не может поддерживаться с $O(\log n)$ ребалансировка работы во время операций вставки и удаления. $\alpha$ Деревья со сбалансированным весом дают целое семейство условий баланса, где каждое левое и правое поддерево имеет по крайней мере часть $\alpha$ от общего веса поддерева. ^{[ 15 ]}^: 62

Типы

Существует несколько самобалансированных бинарных деревьев поиска, включая T-tree , ^{[ 17 ]} треп , ^{[ 18 ]} красно-черное дерево , ^{[ 19 ]} B-дерево , ^{[ 20 ]} 2–3 дерева , ^{[ 21 ]} и дерево воспроизведения . ^{[ 22 ]}

Примеры приложений

Сортировать

Двоичные деревья поиска используются в алгоритмах сортировки, таких как сортировка по дереву , где все элементы вставляются одновременно, а дерево просматривается в заданном порядке. ^{[ 23 ]} BST также используются в быстрой сортировке . ^{[ 24 ]}

Приоритетные операции с очередью

Двоичные деревья поиска используются при реализации очередей приоритетов , используя ключ узла в качестве приоритетов. Добавление новых элементов в очередь повторяет обычную операцию вставки BST, но операция удаления зависит от типа приоритетной очереди: ^{[ 25 ]}

Если это очередь с возрастающим приоритетом, удаление элемента с наименьшим приоритетом выполняется путем обхода BST влево.
Если это очередь с приоритетом по убыванию, удаление элемента с наивысшим приоритетом выполняется путем обхода BST вправо.

См. также

Ссылки

^ Jump up to: ^а ^б Калберсон, Дж.; Манро, JI (1 января 1989 г.). «Объяснение поведения двоичных деревьев поиска при длительных обновлениях: модель и моделирование» . Компьютерный журнал . 32 (1): 68–69. дои : 10.1093/comjnl/32.1.68 .
^ Калберсон, Дж.; Манро, JI (28 июля 1986 г.). «Анализ стандартных алгоритмов удаления в бинарных деревьях поиска с точной подгонкой домена» . Алгоритмика . 5 (1–4). Springer Publishing , Университет Ватерлоо : 297. doi : 10.1007/BF01840390 . S2CID 971813 .
^ П. Ф. Виндли (1 января 1960 г.). «Деревья, леса и переустройство» . Компьютерный журнал . 3 (2): 84. дои : 10.1093/comjnl/3.2.84 .
^ Jump up to: ^а ^б Кнут, Дональд (1998). «Раздел 6.2.3: Сбалансированные деревья». Искусство компьютерного программирования (PDF) . Том. 3 (2-е изд.). Аддисон-Уэсли . стр. 458–481. ISBN 978-0201896855 . Архивировано (PDF) из оригинала 9 октября 2022 г.
^ Пол Э. Блэк, «красно-черное дерево», в Словаре алгоритмов и структур данных [онлайн], Пол Э. Блэк, изд. 12 ноября 2019 г. (по состоянию на 19 мая 2022 г.) с сайта: https://www.nist.gov/dads/HTML/redblack.html.
^ Майерс, Эндрю. «Лекция CS 312: Деревья AVL» . Корнелльский университет , факультет компьютерных наук. Архивировано из оригинала 27 апреля 2021 года . Проверено 19 мая 2022 г.
^ Адельсон-Вельский, Георгий; Лэндис, Евгений (1962). «Алгоритм организации информации». Известия Академии наук СССР (на русском языке). 146 : 263–266. Английский перевод Майрона Дж. Риччи в «Советской математике» - Доклады , 3:1259–1263, 1962.
^ Питасси, Тонианн (2015). «CSC263: Сбалансированные BST, дерево AVL» (PDF) . Университет Торонто , факультет компьютерных наук. п. 6. Архивировано (PDF) из оригинала 14 февраля 2019 г. Проверено 19 мая 2022 г.
^ Jump up to: ^а ^б Тареджа, Рима (13 октября 2018 г.). «Хеширование и столкновение». Структуры данных с использованием C (2-е изд.). Издательство Оксфордского университета . ISBN 9780198099307 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стоун, Клиффорд (2001). Введение в алгоритмы (2-е изд.). МТИ Пресс . ISBN 0-262-03293-7 .
^ Р.А. Мороз; М.М. Петерсон (1 февраля 1982 г.). «Краткая заметка о двоичных деревьях поиска» . Компьютерный журнал . 25 (1). Издательство Оксфордского университета : 158. doi : 10.1093/comjnl/25.1.158 .
^ Цзюньчжоу Хуан. «Проектирование и анализ алгоритмов» (PDF) . Техасский университет в Арлингтоне . п. 12. Архивировано (PDF) из оригинала 13 апреля 2021 г. Проверено 17 мая 2021 г.
^ Рэй, Рэй. «Двоичное дерево поиска» . Университет Лойолы Мэримаунт , факультет компьютерных наук . Проверено 17 мая 2022 г.
^ Торнтон, Алекс (2021). «ICS 46: Двоичные деревья поиска» . Калифорнийский университет в Ирвайне . Архивировано из оригинала 4 июля 2021 года . Проверено 21 октября 2021 г.
^ Jump up to: ^а ^б ^с ^д ^и Брасс, Питер (январь 2011 г.). Расширенная структура данных . Издательство Кембриджского университета . дои : 10.1017/CBO9780511800191 . ISBN 9780511800191 .
^ Блюм, Норберт; Мельхорн, Курт (1978). «О среднем количестве операций ребалансировки в деревьях со сбалансированным весом» (PDF) . Теоретическая информатика . 11 (3): 303–320. дои : 10.1016/0304-3975(80)90018-3 . Архивировано (PDF) из оригинала 9 октября 2022 г.
^ Леман, Тобин Дж.; Кэри, Майкл Дж. (25–28 августа 1986 г.). Исследование структур индексов для систем управления базами данных основной памяти . Двенадцатая Международная конференция по очень большим базам данных (VLDB, 1986). Киото. ISBN 0-934613-18-4 .
^ Арагон, Сесилия Р.; Зайдель, Раймунд (1989), «Рандомизированные деревья поиска» (PDF) , 30-й ежегодный симпозиум по основам информатики , Вашингтон, округ Колумбия: IEEE Computer Society Press, стр. 540–545, doi : 10.1109/SFCS.1989.63531 , ISBN 0-8186-1982-1 , заархивировано (PDF) из оригинала 9 октября 2022 г.
^ Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001). «Красно-черные деревья». Введение в алгоритмы (второе изд.). МТИ Пресс. стр. 273–301 . ISBN 978-0-262-03293-3 .
^ Комер, Дуглас (июнь 1979 г.), «Вездесущее B-дерево», Computing Surveys , 11 (2): 123–137, doi : 10.1145/356770.356776 , ISSN 0360-0300 , S2CID 101673
^ Кнут, Дональд М. (1998). «6.2.4». Искусство компьютерного программирования . Том. 3 (2-е изд.). Эддисон Уэсли. ISBN 9780201896855 . 2–3 дерева, определенные в конце раздела 6.2.3, эквивалентны B-деревьям порядка 3.
^ Слитор, Дэниел Д .; Тарьян, Роберт Э. (1985). «Самонастраивающиеся двоичные деревья поиска» (PDF) . Журнал АКМ . 32 (3): 652–686. дои : 10.1145/3828.3835 . S2CID 1165848 .
^ Нарайанан, Арвинд (2019). «COS226: Двоичные деревья поиска» . Школа инженерии и прикладных наук Принстонского университета . Архивировано из оригинала 22 марта 2021 года . Проверено 21 октября 2021 г. - через cs.princeton.edu.
^ Сюн, Ли. «Связь между двоичными деревьями поиска и быстрой сортировкой» . Оксфордский колледж Университета Эмори , факультет математики и информатики. Архивировано из оригинала 26 февраля 2021 года . Проверено 4 июня 2022 г.
^ Майерс, Эндрю. «CS 2112 Лекции и конспекты: приоритетные очереди и кучи» . Корнелльский университет , факультет компьютерных наук . Архивировано из оригинала 21 октября 2021 года . Проверено 21 октября 2021 г.

Дальнейшее чтение

В этой статье использованы общедоступные материалы из Пол Э. Блэк. «Двоичное дерево поиска» . Словарь алгоритмов и структур данных . НИСТ .
Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001). «12: Двоичные деревья поиска, 15.5: Оптимальные двоичные деревья поиска». Введение в алгоритмы (2-е изд.). МТИ Пресс . стр. 253–272, 356–363. ISBN 0-262-03293-7 .
Джарк, Дуэйн Дж. (3 декабря 2005 г.). «Обход двоичного дерева» . Интерактивная визуализация структуры данных . Университет Мэриленда . Архивировано из оригинала 27 февраля 2014 года . Проверено 30 апреля 2006 г.
Кнут, Дональд (1997). «6.2.2: Поиск в двоичном дереве». Искусство компьютерного программирования . Том. 3: «Сортировка и поиск» (3-е изд.). Аддисон-Уэсли. стр. 426–458. ISBN 0-201-89685-0 .
Долго, Шон. «Двоичное дерево поиска» ( PPT ) . Визуализация структур данных и алгоритмов — подход на основе слайдов PowerPoint . SUNY Онеонта .
Парланте, Ник (2001). «Двоичные деревья» . Образовательная библиотека CS . Стэнфордский университет . Архивировано из оригинала 30 января 2022 г.

Внешние ссылки

Бен Пфафф: Введение в бинарные деревья поиска и сбалансированные деревья . (PDF; 1675 КБ) 2004 г.
Визуализатор двоичного дерева (JavaScript-анимация различных структур данных на основе BT)

[computer_journal89-1] Jump up to: ^а ^б Калберсон, Дж.; Манро, JI (1 января 1989 г.). «Объяснение поведения двоичных деревьев поиска при длительных обновлениях: модель и моделирование» . Компьютерный журнал . 32 (1): 68–69. дои : 10.1093/comjnl/32.1.68 .

[2] Калберсон, Дж.; Манро, JI (28 июля 1986 г.). «Анализ стандартных алгоритмов удаления в бинарных деревьях поиска с точной подгонкой домена» . Алгоритмика . 5 (1–4). Springer Publishing , Университет Ватерлоо : 297. doi : 10.1007/BF01840390 . S2CID 971813 .

[windley60-3] П. Ф. Виндли (1 января 1960 г.). «Деревья, леса и переустройство» . Компьютерный журнал . 3 (2): 84. дои : 10.1093/comjnl/3.2.84 .

[Knuth98-4] Jump up to: ^а ^б Кнут, Дональд (1998). «Раздел 6.2.3: Сбалансированные деревья». Искусство компьютерного программирования (PDF) . Том. 3 (2-е изд.). Аддисон-Уэсли . стр. 458–481. ISBN 978-0201896855 . Архивировано (PDF) из оригинала 9 октября 2022 г.

[5] Пол Э. Блэк, «красно-черное дерево», в Словаре алгоритмов и структур данных [онлайн], Пол Э. Блэк, изд. 12 ноября 2019 г. (по состоянию на 19 мая 2022 г.) с сайта: https://www.nist.gov/dads/HTML/redblack.html.

[6] Майерс, Эндрю. «Лекция CS 312: Деревья AVL» . Корнелльский университет , факультет компьютерных наук. Архивировано из оригинала 27 апреля 2021 года . Проверено 19 мая 2022 г.

[7] Адельсон-Вельский, Георгий; Лэндис, Евгений (1962). «Алгоритм организации информации». Известия Академии наук СССР (на русском языке). 146 : 263–266. Английский перевод Майрона Дж. Риччи в «Советской математике» - Доклады , 3:1259–1263, 1962.

[8] Питасси, Тонианн (2015). «CSC263: Сбалансированные BST, дерево AVL» (PDF) . Университет Торонто , факультет компьютерных наук. п. 6. Архивировано (PDF) из оригинала 14 февраля 2019 г. Проверено 19 мая 2022 г.

[reema18-9] Jump up to: ^а ^б Тареджа, Рима (13 октября 2018 г.). «Хеширование и столкновение». Структуры данных с использованием C (2-е изд.). Издательство Оксфордского университета . ISBN 9780198099307 .

[algo_cormen-10] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Стоун, Клиффорд (2001). Введение в алгоритмы (2-е изд.). МТИ Пресс . ISBN 0-262-03293-7 .

[11] Р.А. Мороз; М.М. Петерсон (1 февраля 1982 г.). «Краткая заметка о двоичных деревьях поиска» . Компьютерный журнал . 25 (1). Издательство Оксфордского университета : 158. doi : 10.1093/comjnl/25.1.158 .

[12] Цзюньчжоу Хуан. «Проектирование и анализ алгоритмов» (PDF) . Техасский университет в Арлингтоне . п. 12. Архивировано (PDF) из оригинала 13 апреля 2021 г. Проверено 17 мая 2021 г.

[13] Рэй, Рэй. «Двоичное дерево поиска» . Университет Лойолы Мэримаунт , факультет компьютерных наук . Проверено 17 мая 2022 г.

[14] Торнтон, Алекс (2021). «ICS 46: Двоичные деревья поиска» . Калифорнийский университет в Ирвайне . Архивировано из оригинала 4 июля 2021 года . Проверено 21 октября 2021 г.

[peter11-15] Jump up to: ^а ^б ^с ^д ^и Брасс, Питер (январь 2011 г.). Расширенная структура данных . Издательство Кембриджского университета . дои : 10.1017/CBO9780511800191 . ISBN 9780511800191 .

[16] Блюм, Норберт; Мельхорн, Курт (1978). «О среднем количестве операций ребалансировки в деревьях со сбалансированным весом» (PDF) . Теоретическая информатика . 11 (3): 303–320. дои : 10.1016/0304-3975(80)90018-3 . Архивировано (PDF) из оригинала 9 октября 2022 г.

[17] Леман, Тобин Дж.; Кэри, Майкл Дж. (25–28 августа 1986 г.). Исследование структур индексов для систем управления базами данных основной памяти . Двенадцатая Международная конференция по очень большим базам данных (VLDB, 1986). Киото. ISBN 0-934613-18-4 .

[18] Арагон, Сесилия Р.; Зайдель, Раймунд (1989), «Рандомизированные деревья поиска» (PDF) , 30-й ежегодный симпозиум по основам информатики , Вашингтон, округ Колумбия: IEEE Computer Society Press, стр. 540–545, doi : 10.1109/SFCS.1989.63531 , ISBN 0-8186-1982-1 , заархивировано (PDF) из оригинала 9 октября 2022 г.

[Cormen2001-19] Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2001). «Красно-черные деревья». Введение в алгоритмы (второе изд.). МТИ Пресс. стр. 273–301 . ISBN 978-0-262-03293-3 .

[20] Комер, Дуглас (июнь 1979 г.), «Вездесущее B-дерево», Computing Surveys , 11 (2): 123–137, doi : 10.1145/356770.356776 , ISSN 0360-0300 , S2CID 101673

[21] Кнут, Дональд М. (1998). «6.2.4». Искусство компьютерного программирования . Том. 3 (2-е изд.). Эддисон Уэсли. ISBN 9780201896855 . 2–3 дерева, определенные в конце раздела 6.2.3, эквивалентны B-деревьям порядка 3.

[22] Слитор, Дэниел Д .; Тарьян, Роберт Э. (1985). «Самонастраивающиеся двоичные деревья поиска» (PDF) . Журнал АКМ . 32 (3): 652–686. дои : 10.1145/3828.3835 . S2CID 1165848 .

[23] Нарайанан, Арвинд (2019). «COS226: Двоичные деревья поиска» . Школа инженерии и прикладных наук Принстонского университета . Архивировано из оригинала 22 марта 2021 года . Проверено 21 октября 2021 г. - через cs.princeton.edu.

[24] Сюн, Ли. «Связь между двоичными деревьями поиска и быстрой сортировкой» . Оксфордский колледж Университета Эмори , факультет математики и информатики. Архивировано из оригинала 26 февраля 2021 года . Проверено 4 июня 2022 г.

[25] Майерс, Эндрю. «CS 2112 Лекции и конспекты: приоритетные очереди и кучи» . Корнелльский университет , факультет компьютерных наук . Архивировано из оригинала 21 октября 2021 года . Проверено 21 октября 2021 г.

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

v т и Древовидные структуры данных
Search trees (dynamic sets/associative arrays)	2–3 2–3–4 AA (a,b) AVL B B+ B* B^x (Optimal) Binary search Dancing HTree Interval Order statistic Palindrome (Left-leaning) Red–black Scapegoat Splay T Treap UB Weight-balanced
Heaps	Binary Binomial Brodal d-ary Fibonacci Leftist Pairing Skew binomial Skew van Emde Boas Weak
Tries	Ctrie C-trie (compressed ADT) Hash Radix Suffix Ternary search X-fast Y-fast
Spatial data partitioning trees	Ball BK BSP Cartesian Hilbert R k-d (implicit k-d) M Metric MVP Octree PH Priority R Quad R R+ R* Segment VP X
Other trees	Cover Exponential Fenwick Finger Fractal tree index Fusion Hash calendar iDistance K-ary Left-child right-sibling Link/cut Log-structured merge Merkle PQ Range SPQR Top

v т и Структуры данных
Types	Collection Container
Abstract	Associative array Multimap Retrieval Data Structure List Stack Queue Double-ended queue Priority queue Double-ended priority queue Set Multiset Disjoint-set
Arrays	Bit array Circular buffer Dynamic array Hash table Hashed array tree Sparse matrix
Linked	Association list Linked list Skip list Unrolled linked list XOR linked list
Trees	B-tree Binary search tree AA tree AVL tree Red–black tree Self-balancing tree Splay tree Heap Binary heap Binomial heap Fibonacci heap R-tree R* tree R+ tree Hilbert R-tree Trie Hash tree
Graphs	Binary decision diagram Directed acyclic graph Directed acyclic word graph
List of data structures