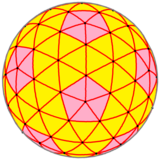
Гексапентакис усеченный икосаэдр

Гексапентакис усеченный икосаэдр

Обозначение Конвея	кти
Геодезический многогранник	{3,5+} _3,0
Лица	180
Края	270
Вершины	92
Конфигурация лица	(60) В5.6.6 (120) Версия 6.6.6
Группа симметрии	Икосаэдрический ( I _h )
Двойной многогранник	Усеченный пентакис додекаэдр
Характеристики	выпуклый

— Усеченный икосаэдр гексапентакиса выпуклый многогранник , построенный как расширенный усеченный икосаэдр . Это геодезический многогранник {3,5+} _3,0 , пятивалентные вершины которого разделены расстоянием от края в 3 шага.

Строительство

Геодезические многогранники строятся путем разделения граней более простых многогранников и последующего проецирования новых вершин на поверхность сферы. Геодезический многогранник имеет прямые края и плоские грани, которые приближаются к сфере, но он также может быть выполнен в виде сферического многогранника ( мозаика на сфере ) с истинно геодезическими изогнутыми краями на поверхности сферы. и сферические треугольные грани.

Конвей	u ₃ I = (kt)I	(k5)k6tI	(к)тИ	Сферический кТИ
Изображение
Форма	3-частотный разделенный икосаэдр	1-частотный разделенный гексакис усеченный икосаэдр	1-частотный разделенный усеченный икосаэдр	Сферический многогранник

Связанные многогранники

Многогранник	Усеченный икосаэдр	#Пентакис усеченный икосаэдр	#Гексакис усеченный икосаэдр	Гексапентакис усеченный икосаэдр
Изображение
Конвей	из	k5tI	к6ти	k5k6tI

Усеченный икосаэдр Пентакиса

Усеченный икосаэдр Пентакиса

Обозначение Конвея	k5tI
Лица	132: 60 треугольников 20 шестиугольников
Края	90
Вершины	72
Группа симметрии	Икосаэдрический ( I _h )
Двойной многогранник	Пятиусеченный пентакис додекаэдр
Характеристики	выпуклый

— Усеченный икосаэдр пентакиса это выпуклый многогранник, построенный как расширенный усеченный икосаэдр , добавляющий пирамиды к 12 пятиугольным граням, создавая 60 новых треугольных граней.

Геометрически он подобен икосаэдру , в котором 20 треугольных граней разделены центральным шестиугольником и тремя угловыми треугольниками.

Двойной

Его двойственный многогранник можно назвать пентаусеченным пентакис додекаэдром , додекаэдром , вершины которого увеличены пятиугольными пирамидами, а затем усечены вершины этих пирамид или добавлены пятиугольные призмы к каждой грани додекаэдра. Это развертка додекаэдрической призмы .

Гексакис усеченный икосаэдр

Гексакис усеченный икосаэдр

Обозначение Конвея	к6ти
Лица	132: 120 треугольников 12 пятиугольников
Края	210
Вершины	80
Группа симметрии	Икосаэдрический ( I _h )
Двойной многогранник	Шестиусеченный пентакис додекаэдр
Характеристики	выпуклый

Шестиугольный усеченный икосаэдр — это выпуклый многогранник, построенный как расширенный усеченный икосаэдр , в котором к 20 шестиугольным граням добавляются пирамиды, создавая 120 новых треугольных граней.

Визуально он похож на хиральный курносый додекаэдр, имеющий 80 треугольников и 12 пятиугольников.

Двойной

Двойственный многогранник можно рассматривать как шестиусеченный пентакис-додекаэдр , додекаэдр, грани которого дополнены пятиугольными пирамидами ( пентакис-додекаэдр ), а затем его 6-валентные вершины усечены.

Он имеет те же группы неправильных пятиугольников, что и пятиугольный шестиконтаэдр .

См. также

Гексатетракис усеченный октаэдр

Ссылки

Энтони Пью, Многогранники: визуальный подход , 1976, Глава 6. Геодезические многогранники Р. Бакминстера Фуллера и родственные многогранники.
Веннингер, Магнус (1979), Сферические модели , Издательство Кембриджского университета , ISBN 978-0-521-29432-4 , MR 0552023 , заархивировано из оригинала 4 июля 2008 г. Перепечатано Dover, 1999 г. ISBN 978-0-486-40921-4

Внешние ссылки

Генератор многогранников VTML Попробуйте «ktI» ( обозначение многогранника Конвея )