Гравитационный поезд

Гравитационный поезд — это теоретическое средство передвижения, предназначенное для передвижения между двумя точками на поверхности сферы по прямому туннелю , соединяющему две точки через внутреннюю часть сферы.

В большом теле, таком как планета , этому поезду можно было бы позволить ускоряться, используя только силу тяжести , поскольку в течение первой половины пути (от точки отправления до середины) тяга вниз к центру тяжести потянул бы его к месту назначения. Во второй половине пути ускорение было бы в противоположном направлении относительно траектории, но, пренебрегая эффектами трения , приобретенная ранее скорость преодолела бы это замедление, и в результате скорость поезда достигла бы нуля при примерно в тот момент, когда поезд достиг пункта назначения. ^[1]^{[ нужен лучший источник ]}

Происхождение концепции

В 17 веке британский учёный Роберт Гук изложил идею объекта, ускоряющегося внутри планеты в письме Исааку Ньютону . Проект гравитационного поезда всерьез был представлен Французской академии наук в XIX веке. Ту же идею, без всякого расчета, предложил Льюис Кэрролл в 1893 году в книге «Заключение Сильви и Бруно» . Идея была вновь открыта в 1960-х годах, когда физик Пол Купер опубликовал в Американском журнале физики статью , в которой предлагал рассмотреть возможность использования гравитационных поездов в качестве будущего транспортного проекта. ^[2]

Математические соображения

В предположении о сферической планете с однородной плотностью и без учета релятивистских эффектов , а также трения гравитационный поезд имеет следующие свойства: ^[3]

Продолжительность путешествия зависит только от плотности планеты и гравитационной постоянной , но не от диаметра планеты.
Максимальная скорость достигается в средней точке траектории.

Для гравитационных поездов между точками, которые не являются антиподами друг друга, справедливы следующие условия:

Самый короткий туннель времени через однородную Землю — это гипоциклоида ; в частном случае двух противоположных точек гипоциклоида вырождается в прямую линию.
Все прямолинейные гравитационные поезда на данной планете совершают путь совершенно одинаково за время (то есть независимо от того, где на поверхности расположены две конечные точки его траектории).

Конкретно на планете Земля , поскольку движение гравитационного поезда является проекцией движения спутника на очень низкой околоземной орбите на линию, оно имеет следующие параметры:

Время путешествия равно 2530,30 секунды (почти 42,2 минуты, половина периода спутника на низкой околоземной орбите), если предположить, что Земля представляет собой идеальную сферу с однородной плотностью.
Принимая во внимание реалистичное распределение плотности внутри Земли, известное из предварительной эталонной модели Земли , ожидаемое время падения сокращается с 42 до 38 минут. ^[4]

Для сравнения: самая глубокая на данный момент скважина — это Кольская сверхглубокая скважина с истинной глубиной 12 262 метра; Чтобы преодолеть расстояние между Лондоном и Парижем (350 км) по гипоциклоидной дороге, потребуется создать яму глубиной 111 408 метров. Такая глубина не только в 9 раз больше, но и потребовала бы туннеля, проходящего через мантию Земли .

Математический вывод

Используя приближения, согласно которым Земля имеет идеальную сферическую форму и однородную плотность. $\rho$ , а тот факт, что внутри однородной полой сферы нет гравитации, ускорение свободного падения $a$ испытываемое телом внутри Земли, пропорционально отношению расстояния от центра $r$ к радиусу Земли $R$ . Это потому, что под землей на расстоянии $r$ из центра все равно, что находиться на поверхности планеты радиуса $r$ , внутри полой сферы, которая ничего не дает.

a={\frac {GM}{r^{2}}}={\frac {G\rho V}{r^{2}}}={\frac {G\rho {\frac {4}{3}}\pi \,r^{3}}{r^{2}}}=G\rho {\frac {4}{3}}\pi \,r

На поверхности, $r=R$ , поэтому гравитационное ускорение равно $g=G\rho {\frac {4}{3}}\pi \,R$ . Следовательно, гравитационное ускорение при $r$ является

a={\frac {r}{R}}\,g

Диаметральный путь к антиподам

В случае прямой линии, проходящей через центр Земли, ускорение тела равно ускорению силы тяжести: оно свободно падает прямо вниз. Мы начинаем падать на поверхность, поэтому со временем $t$ (считая ускорение и скорость положительными вниз):

r_{t}=R-\int _{0}^{t}v_{t}\,dt=R-\int _{0}^{t}\int _{0}^{t}a_{t}\,dt\,dt

Дифференцируем дважды:

{\frac {d^{2}r}{dt^{2}}}=-a_{t}=-{\frac {r}{R}}\,g=-\omega ^{2}\,r

где $\omega ={\sqrt {\frac {g}{R}}}$ . Этот класс задач, в которых действует возвращающая сила, пропорциональная смещению от нуля, имеет общие решения вида $r=k\cos(\omega t+\varphi )$ и описывает простое гармоническое движение, например, пружины или маятника .

В этом случае $r_{t}=R\cos {\sqrt {\frac {g}{R}}}\,t$ так что $r_{0}=R$ , мы начинаем на поверхности в нулевой момент времени и вечно колеблемся взад и вперед.

Время пути к антиподам составляет половину одного цикла этого осциллятора, то есть время рассуждения $\cos {\sqrt {\frac {g}{R}}}\,t$ вымести ${\pi }$ радианы. Используя простые приближения $g=10{\text{ m}}/{\text{s}}^{2},R=6500{\text{ km}}$ это время

T={\frac {\pi }{\omega }}={\frac {\pi }{\sqrt {\frac {g}{R}}}}\approx {\frac {3.1415926}{\sqrt {\frac {10}{6500000}}}}\approx 2532{\text{ s}}

Прямой путь между двумя произвольными точками

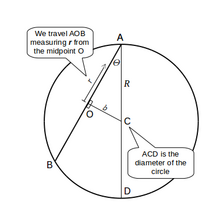
Для более общего случая прямой линии между любыми двумя точками на поверхности сферы мы вычисляем ускорение тела, когда оно движется без трения по своей прямой траектории.

Тело движется по АОВ, где О — середина пути и ближайшая точка к центру Земли на этом пути. На расстоянии $r$ на этом пути сила тяжести зависит от расстояния $x$ к центру Земли, как указано выше. Использование сокращений $b=R\sin \theta$ для длины OC:

g_{r}={\frac {x}{R}}\,g={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g

Результирующее ускорение тела, т.к. оно на без трения наклонная поверхность , есть $g_{r}\cos \varphi$ :

Схема сил на гравитационном поезде на недиаметрическом прямолинейном пути

a_{r}=g_{r}\cos \varphi ={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g\cos \varphi

Но $\cos \varphi$ является $r/x={\frac {r}{\sqrt {r^{2}+b^{2}}}}$ , поэтому заменив:

a_{r}={\frac {\sqrt {r^{2}+b^{2}}}{R}}\,g\,{\frac {r}{\sqrt {r^{2}+b^{2}}}}={\frac {r}{R}}\,g

что то же самое для этого нового $r$ , расстояние вдоль AOB от O, что касается $r$ в диаметральном случае вдоль ACD. Таким образом, оставшийся анализ остается таким же, учитывая начальное условие, что максимальный $r$ является $R\cos \theta =AO$ полное уравнение движения

r_{t}=R\cos \theta \cos {\sqrt {\frac {g}{R}}}\,t

Постоянная времени $\omega ={\sqrt {\frac {g}{R}}}$ то же самое, что и в диаметральном случае, поэтому время в пути по-прежнему составляет 42 минуты; просто все расстояния и скорости масштабируются по константе $\cos \theta$ .

Зависимость от радиуса планеты

Постоянная времени $\omega$ зависит только от ${\frac {g}{R}}$ поэтому, если мы расширим это, мы получим

{\frac {g}{R}}={\frac {GM/R^{2}}{R}}={\frac {GM}{R^{3}}}={\frac {G\rho \,V}{R^{3}}}={\frac {G\rho \,{\frac {4}{3}}\pi \,R^{3}}{R^{3}}}=G\rho \,{\frac {4}{3}}\pi

которая зависит только от гравитационной постоянной и $\rho$ плотность . планеты Размер планеты не имеет значения; время в пути одинаково, если плотность одинакова.

В художественной литературе

В фильме 2012 года « Вспомнить все » гравитационный поезд под названием «Падение» проходит через центр Земли, курсируя между Западной Европой и Австралией. ^[5]^[6]

См. также

Ссылки

^ Ньютон, Исаак. Математические основы натуральной философии .
^ «Куда угодно за 42 минуты» . Время . 11 февраля 1966 года.
^ Робин Дэвис: несбыточная мечта физика ^{[ постоянная мертвая ссылка ]}
^ Клоц, Александр Р. (2015). «Гравитационный туннель в неоднородной Земле». Американский журнал физики . 83 (3): 231–237. arXiv : 1308.1342 . Бибкод : 2015AmJPh..83..231K . дои : 10.1119/1.4898780 . S2CID 118572386 .
^ Мартинес, Джейсон (13 августа 2012 г.). «Наука полной памяти» . Блог Вольфрам-Альфа . Проверено 30 марта 2018 г.
^ Ротман, Лили (6 августа 2012 г.). «Внимание, спойлер: дыра длиной 8000 миль в Total Recall» . Время . Проверено 30 марта 2018 г.

Описание концепции «Гравитационный поезд» и математическое решение ( веб-страница Александра Еременко в Университете Пердью ).

Внешние ссылки

[1] Ньютон, Исаак. Математические основы натуральной философии .

[2] «Куда угодно за 42 минуты» . Время . 11 февраля 1966 года.

[3] Робин Дэвис: несбыточная мечта физика ^{[ постоянная мертвая ссылка ]}

[4] Клоц, Александр Р. (2015). «Гравитационный туннель в неоднородной Земле». Американский журнал физики . 83 (3): 231–237. arXiv : 1308.1342 . Бибкод : 2015AmJPh..83..231K . дои : 10.1119/1.4898780 . S2CID 118572386 .

[5] Мартинес, Джейсон (13 августа 2012 г.). «Наука полной памяти» . Блог Вольфрам-Альфа . Проверено 30 марта 2018 г.

[6] Ротман, Лили (6 августа 2012 г.). «Внимание, спойлер: дыра длиной 8000 миль в Total Recall» . Время . Проверено 30 марта 2018 г.

[1]

[2]

[3]

[4]

[5]

[6]