Средняя абсолютная ошибка

Не путать со средним абсолютным отклонением или средней абсолютной разницей .

В статистике между парными наблюдениями , средняя абсолютная ошибка ( MAE ) — это мера ошибок выражающими одно и то же явление. Примеры Y и X включают сравнение прогнозируемого и наблюдаемого, последующего времени и начального времени, а также сравнения одного метода измерения с альтернативным методом измерения. MAE рассчитывается как сумма абсолютных ошибок (т. е. Манхэттенского расстояния ), деленная на размер выборки : $$\mathrm {MAE} ={\frac {\sum _{i=1}^{n}\left|y_{i}-x_{i}\right|}{n}}={\frac {\sum _{i=1}^{n}\left|e_{i}\right|}{n}}.$$Таким образом, это среднее арифметическое абсолютных ошибок. $|e_{i}|=|y_{i}-x_{i}|$, где $y_{i}$ это предсказание и $x_{i}$ истинная ценность. Альтернативные формулировки могут включать относительные частоты в качестве весовых коэффициентов. Средняя абсолютная ошибка использует тот же масштаб, что и измеряемые данные. Это известно как мера точности, зависящая от масштаба, и поэтому ее нельзя использовать для сравнения прогнозируемых значений, использующих разные масштабы. Средняя абсолютная ошибка — это распространенная мера ошибки прогноза при анализе временных рядов . иногда используется в путанице с более стандартным определением среднего абсолютного отклонения . Такая же путаница существует и в более широком смысле.

Разногласия по количеству и разногласия по распределению

Две точки данных, для которых разногласие по количеству равно 0, а разногласие по распределению равно 2 как для MAE, так и для RMSE.

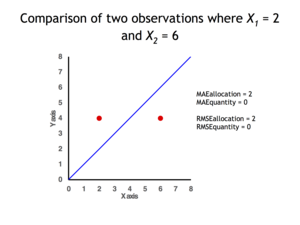
В дистанционном зондировании MAE иногда выражается как сумма двух компонентов: несогласия по количеству и несогласия по распределению. Количественное расхождение представляет собой абсолютное значение средней ошибки: $$\left|{\frac {\sum _{i=1}^{n}y_{i}-x_{i}}{n}}\right|.$$Разногласия в распределении — это MAE минус разногласия по количеству.

Также можно определить типы различий, взглянув на $(x,y)$ сюжет. Количественная разница существует, когда среднее значение X не равно среднему значению Y. Разница в распределении существует тогда и только тогда, когда точки находятся по обе стороны от идентификационной линии.

Сопутствующие меры

Средняя абсолютная ошибка — это один из многих способов сравнения прогнозов с их конечными результатами. Хорошо зарекомендовавшими себя альтернативами являются средняя абсолютная масштабированная ошибка (MASE), средняя абсолютная логарифмическая ошибка (MALE) и среднеквадратическая ошибка . Все они суммируют результаты таким образом, чтобы не принимать во внимание направления завышения или занижения прогнозов; мерой, которая действительно уделяет этому внимание, является средняя знаковая разность .

Если модель прогнозирования должна быть подобрана с использованием выбранной меры производительности, в том смысле, что метод наименьших квадратов связан со среднеквадратичной ошибкой , эквивалентом средней абсолютной ошибки являются наименьшие абсолютные отклонения .

MAE не идентично среднеквадратичной ошибке (RMSE), хотя некоторые исследователи сообщают и интерпретируют ее именно так. MAE концептуально проще и его легче интерпретировать, чем RMSE: это просто среднее абсолютное расстояние по вертикали или горизонтали между каждой точкой диаграммы рассеяния и линией Y=X. Другими словами, MAE — это средняя абсолютная разница между X и Y. Более того, каждая ошибка вносит свой вклад в MAE пропорционально абсолютному значению ошибки. В этом отличие от RMSE, который предполагает возведение разностей в квадрат, так что несколько больших различий увеличивают RMSE в большей степени, чем MAE.

Свойство оптимальности

Средняя абсолютная ошибка действительной переменной c по отношению к случайной величине   X равна $$E(\left|X-c\right|).$$ , что распределение вероятностей X таково, что вышеуказанное ожидание существует, тогда m является медианой X При условии тогда и только тогда, когда m является минимизатором средней абсолютной ошибки по отношению к X . В частности, m является выборочной медианой тогда и только тогда, когда m минимизирует среднее арифметическое абсолютных отклонений.

В более общем смысле медиана определяется как минимум $$E(|X-c|-|X|),$$как обсуждалось в разделе «Многомерная медиана» (и, в частности, в разделе «Пространственная медиана» ). Это основанное на оптимизации определение медианы полезно при статистическом анализе данных, например, при k кластеризации -медиан .

Доказательство оптимальности

Утверждение: классификатор, минимизирующий $\mathbb {E} |y-{\hat {y}}|$ является ${\hat {f}}(x)={\text{Median}}(y|X=x)$ .

Доказательство:

Функции потерь для классификации : $${\begin{aligned}L&=\mathbb {E} [|y-a||X=x]\\&=\int _{-\infty }^{\infty }|y-a|f_{Y|X}(y)\,dy\\&=\int _{-\infty }^{a}(a-y)f_{Y|X}(y)\,dy+\int _{a}^{\infty }(y-a)f_{Y|X}(y)\,dy.\\\end{aligned}}$$ отношению к дает Дифференциация по $${\frac {\partial }{\partial a}}L=\int _{-\infty }^{a}f_{Y|X}(y)\,dy+\int _{a}^{\infty }-f_{Y|X}(y)\,dy=0.$$Это означает $$\int _{-\infty }^{a}f(y)\,dy=\int _{a}^{\infty }f(y)\,dy.$$Следовательно, $$F_{Y|X}(a)=0.5.$$

См. также

• Наименьшие абсолютные отклонения
• Расстояние Манхэттен
• Средняя абсолютная процентная ошибка
• Средняя процентная ошибка
• Симметричная средняя абсолютная процентная ошибка