Комментариолус

Комментарий к гипотезам небесных движений, выдвинутых им самим

г-жа Австрийская национальная библиотека, 10530, ф. 34р
Автор	Николай Коперник
Язык	латинский
Предмет	Астрономия
Дата публикации	1514

« Комментариол » ( «Маленький комментарий» ) — это краткий очерк Николая Коперника ранней версии его революционной гелиоцентрической теории Вселенной. После дальнейшего долгого развития своей теории Коперник опубликовал зрелую версию в 1543 году в своем знаковом труде « De Revolutionibus orbium coelestium» ( «О вращении небесных сфер »).

Коперник написал « Комментарий» на латыни к 1514 году и разослал копии своим друзьям и коллегам. Таким образом, оно стало известно среди современников Коперника, хотя при его жизни оно так и не было напечатано. В 1533 году Иоганн Альбрехт Видманштеттер серию лекций, прочитал в Риме излагающих теорию Коперника. Папа Климент VII и несколько католических кардиналов слушали лекции и заинтересовались теорией. 1 ноября 1536 года Николаус фон Шенберг , архиепископ Капуи , а с предыдущего года кардинал, написал Копернику из Рима и попросил у него копию его сочинений «как можно скорее».

Хотя копии « Комментариола» некоторое время распространялись после смерти Коперника, впоследствии он канул в безвестность, и о его предыдущем существовании оставалось известно лишь косвенно, пока сохранившаяся рукописная копия не была обнаружена и опубликована во второй половине девятнадцатого века.

Краткое содержание

«Комментариол» разделен на восемь разделов (или глав), все из которых, кроме первой, имеют краткие описательные названия. После краткого введения в первом разделе излагаются семь постулатов, на основе которых Коперник предлагает показать, что видимое движение планет можно объяснить систематически.

Семь постулатов

1. Не все небесные тела вращаются вокруг одной точки.
2. Центр Земли — это центр лунной сферы — орбиты Луны вокруг Земли.
3. Все сферы вращаются вокруг Солнца , которое находится недалеко от центра Вселенной.
4. Расстояние между Землей и Солнцем составляет незначительную долю расстояния от Земли и Солнца до звезд, поэтому параллакс не наблюдается. у звезд
5. Звезды неподвижны; их видимое суточное движение вызвано суточным вращением Земли.
6. Земля движется по сфере вокруг Солнца, вызывая очевидную ежегодную миграцию Солнца; Земля имеет более одного движения.
7. Орбитальное движение Земли вокруг Солнца вызывает кажущееся обратное направление движения планет.

Остальные семь разделов по порядку озаглавлены: « Порядок сфер» ( «Порядок сфер» ), «Кажущиеся движения Солнца» ( «Кажущиеся движения Солнца » ), о которых идет речь ( «Равное движение должно быть измерено ». не по равноденствиям, а по неподвижным звездам» ), De Luna ( « » ) , De tribus Superioribus: ( «Внешние планеты: Saturno , Jove et Mars Луна Сатурн, Юпитер и Марс »), De Venere ( « Венера » ) и Де Меркурио ( « Меркурий » ).

Порядок сфер

В этом разделе небесные сферы даны в порядке от самого внешнего к самому внутреннему.Самая внешняя сфера — это сфера неподвижных звезд, которая остается совершенно неподвижной. Затем следуют Сатурн, Юпитер, Марс, Земля, Венера и Меркурий, каждый из которых вращается вокруг Солнца с запада на восток с последовательно более короткими периодами обращения: Сатурн находится между 29 и 30 годами, Юпитер - между 11 и 12, Марс - между 2 годами. и 3, у Земли ровно один, у Венеры между 8 и 9 месяцами, и Меркурий между 2 и 3 месяцами. Однако сфера Луны обращается вокруг Земли за один месяц и движется вместе с ней вокруг Солнца, как эпицикл .

Видимое движение Солнца

В этом разделе объясняется, как видимое движение Солнца могло возникнуть в результате трех отдельных движений Земли. Первое движение представляет собой равномерный оборот с периодом один год с запада на восток по круговой орбите, центр которой смещен от Солнца на 1/25 радиуса орбиты.

Второе движение — это суточное вращение вокруг оси, проходящей через центр Земли и наклоненной под углом около 23°. 1 ⁄ 2 ° к перпендикуляру к плоскости его орбиты.

Третье движение — это прецессия оси вращения Земли вокруг оси, перпендикулярной плоскости ее орбиты. Коперник определил скорость этой прецессии по отношению к радиальной линии от Земли до центра ее орбиты как чуть меньше года, подразумевая направление с запада на восток. По отношению к неподвижным звездам эта прецессия очень медленная и в противоположном направлении — с востока на запад — и объясняет явление прецессии равноденствий .

Равномерное движение следует измерять не по равноденствиям, а по неподвижным звездам.

Здесь Коперник утверждает, что движение точек равноденствия и небесных полюсов не было равномерным, и утверждает, что, следовательно, их не следует использовать для определения системы отсчета, относительно которой измеряются движения планет, и что периоды различных Движения планет можно определить более точно, если эти движения измеряются относительно неподвижных звезд. Он утверждает, что обнаружил, что продолжительность звездного года всегда составляла 365 дней 6 часов 10 минут.

Луна

Схема орбиты Луны, описанная Коперником в его «Комментариолах».

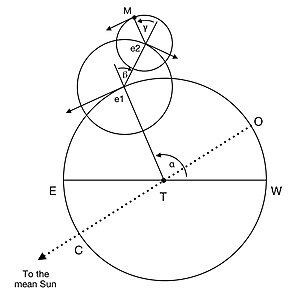
Включая годовой оборот вокруг Солнца, который Луна делит с Землей в своей системе, Коперник объясняет движение Луны как состоящее из пяти независимых движений. Его движение вокруг Земли происходит в плоскости, наклоненной под углом 5° к плоскости земной орбиты и прецессирующей с востока на запад вокруг оси, перпендикулярной этой плоскости, с периодом от 18 до 19 лет. относительно неподвижных звезд. Остальные три движения, происходящие внутри этой орбитальной плоскости, изображены на схеме справа. Первый из них — это центр первого и более крупного из двух эпициклов , центр которого (представленный точкой e1 на диаграмме) движется равномерно с запада на восток по окружности деферента с центром на Земле (представленного точкой T). на схеме) с периодом в один драконовский месяц . Центр второго, меньшего эпицикла (представлен на диаграмме точкой е2) движется равномерно с востока на запад по окружности первого так, что период угла β на диаграмме составляет один аномалистический месяц .

Сама Луна, представленная на схеме точкой М, движется равномерно с запада на восток по окружности второго эпицикла так, что период угла γ составляет половину синодического месяца . Коперник утверждает, что всякий раз, когда точка e1 лежит на линии, соединяющей Землю с центром ее орбиты (представленной на диаграмме пунктирной линией OTC, из которых только точка T здесь находится в плоскости орбиты Луны), Луна M будет лежат точно между e1 и e2. Однако это может произойти только один раз в 19 лет, когда эта линия совпадает с линией узлов WTE. В других случаях она не лежит в плоскости орбиты Луны, и поэтому точка е1 не может пройти через нее. В общем, тогда, хотя Луна будет близка к соединению или оппозиции к Солнцу, когда бы она ни находилась точно между е1 и е2, эти события не будут точно одновременными.

Соотношение, которое Коперник принял за относительную длину малого эпицикла, большого эпицикла и деферента, составляет 4:19:180.

Внешние планеты Сатурн, Юпитер и Марс.

Теории Коперника о движении внешних планет, которые дает Коперник в «Комментариях», имеют одинаковую общую структуру и различаются только значениями различных параметров, необходимых для полного определения их движения. Их орбиты не копланарны с орбитой Земли, но имеют общий центр и лежат в плоскостях, лишь слегка наклоненных к плоскости орбиты Земли. В отличие от орбитальной плоскости Луны, плоскости орбиты высших планет не прецессируют. Однако их наклоны к плоскости орбиты Земли колеблются в пределах 0°10′ и 1°50′ для Марса, 1°15′ и 1°40′ для Юпитера и 2°15′ и 2°40′ для Юпитера. Сатурн. Хотя Коперник предполагает, что эти колебания происходят вокруг линий узлов орбит , которые, по его мнению, остаются фиксированными, механизм, который он использует для их моделирования, действительно вызывает также крошечные колебания в линиях узлов. Как позже указывал Кеплер, необходимость допустить колебания наклонов плоскостей орбит внешних планет является результатом того, что Коперник считал их проходящими через центр орбиты Земли. Если бы он принял их за проходящие через Солнце, ему не пришлось бы вводить эти колебания.

Схема орбиты внешней планеты, описанная Коперником в его «Комментариоле».

Как и движение Луны, движение внешних планет, представленное на диаграмме справа, производится комбинацией деферентного и двух эпициклов. Центр первого, большего из двух эпициклов, представленный на диаграмме точкой e1, равномерно вращается с запада на восток вокруг окружности деферента, центром которого является центр земной орбиты, представленный точкой S на диаграмме. диаграмма с периодом относительно неподвижных звезд, как указано в разделе «Порядок сфер» выше.

Центр второго эпицикла, представленный на диаграмме точкой е2, равномерно вращается с востока на запад вокруг окружности первого с тем же периодом относительно радиальной линии, соединяющей S с е1. Вследствие этого направление радиальной линии, соединяющей е1 и е2, остается фиксированным относительно неподвижных звезд, параллельно линии апсид планеты EW, а точка е2 описывает эксцентрическую окружность. радиус которого равен радиусу деферента, и чей центр, представленный точкой О на диаграмме, смещен от центра деферента на радиус первого эпицикла. В своей более поздней работе « De Revolutionibus orbium coelestium » Коперник напрямую использует этот эксцентрический круг, а не представляет его как комбинацию деферента и эпицикла.

ровно одну треть радиуса первого, со скоростью, вдвое превышающей скорость вращения e1 вокруг S. Сама планета, представленная на диаграмме точкой P, равномерно вращается с запада на восток вокруг окружности второго эпицикла, радиус которого составляет Это устройство позволило Копернику отказаться от экванты — широко критикуемой особенности теорий Клавдия Птолемея о движении внешних планет. В гелиоцентрической версии моделей Птолемея его эквант будет лежать в точке Q на диаграмме, смещенной по линии апсид на восток-запад от точки S на расстояние, в три раза превышающее радиус первого эпицикла Коперника. Центр деферента планеты с тем же радиусом, что и у Коперника, будет лежать в точке C, на полпути между S и Q. Сама планета будет лежать в точке пересечения этого деферента с линией QP. Хотя эта точка точно совпадает с P только тогда, когда они обе находятся в апсиде , разница между их позициями всегда ничтожна по сравнению с неточностями, присущими обеим теориям.

Для отношения радиусов деферентов внешних планет к радиусу Земли Комментариол дает 1. 13/25 5 для Марса , 13/60 для Юпитера 9 и 7/30 . для Сатурна Для отношений радиусов их деферентов к радиусам большего из их эпициклов это дает 6 138/167 12 для Марса , 553/606 для 11 Юпитера и 859/1181 . Сатурна для

Венера

В последних двух разделах Коперник говорит о Венере и Меркурии. Первый имеет систему кругов и совершает оборот за 9 месяцев.

Меркурий

Орбиту Меркурия труднее изучать, чем орбиту любой другой планеты, поскольку она видна всего несколько дней в году. Меркурий, как и Венера, имеет два эпицикла, один больше другого. Чтобы совершить революцию, требуется почти три месяца.

Ссылки

Библиография

• Барди, А. (2024). Коперник и аксиоматика. В: Шрираман Б. (ред.) Справочник по истории и философии математической практики. Спрингер, Чам. https://doi.org/10.1007/978-3-031-40846-5_110
• Коперник, Николай (1992), Чарторыйский, Павел (ред.), Рукописи второстепенных произведений Николая Коперника; факсимиле , Краков: Польская академия наук, ISBN  83-01-10562-3
• Дрейер, Джон Луи Эмиль (1890). Тихо Браге; Картина научной жизни и творчества в шестнадцатом веке . Эдинбург: Адам и Чарльз Блэк .
• Джинджерич, Оуэн (2004). Книга, которую никто не читал . Лондон: Уильям Хайнеманн. ISBN  0-434-01315-3 .
• Годду, Андре (2010). Коперник и аристотелевская традиция . Лейден, Нидерланды: Brill. ISBN  978-90-04-18107-6 .
• Койре, Александр (1973). Астрономическая революция: Коперник – Кеплер – Борелли . Итака, Нью-Йорк: Издательство Корнельского университета . ISBN  0-8014-0504-1 .
• Розен, Эдвард (2004) [1939]. Три коперниканских трактата: Комментарий Коперника; Письмо против Вернера; Narratio Prima of Rheticus (второе издание, исправленное издание). Нью-Йорк, штат Нью-Йорк: Dover Publications, Inc.
• Свердлов, Ноэль М. (декабрь 1973 г.), «Вывод и первый набросок планетарной теории Коперника».
  Перевод Commentariolus с комментариями.», Proceedings of the American Philosophical Society , 117 (6): 423–512.
• Торен, Виктор Э. (1990). Лорд Ураниборга . Кембридж: Издательство Кембриджского университета . ISBN  0-521-35158-8 .

Внешние ссылки

• http://www.fh-augsburg.de/%7Eharsch/Chronologia/Lspost16/Copernicus/kop_c00.html Полный латинский текст онлайн в Bibliotheca Augustana.
• Английский перевод Эдварда Розена (2004, стр. 57–65))
• https://web.archive.org/web/20090803215559/http://www.geocities.com/soho/gallery/8084/copernicus.htm