Сверточный код

В телекоммуникациях сверточный код — это тип кода с исправлением ошибок , который генерирует символы четности посредством скользящего применения булевой полиномиальной функции к потоку данных. Скользящее приложение представляет собой «свертку» кодера над данными, что приводит к появлению термина «сверточное кодирование». Скользящая природа сверточных кодов облегчает решетчатое декодирование с использованием неизменяемой во времени решетки. Независимое от времени решетчатое декодирование позволяет сверточным кодам быть декодированными с мягким решением с максимальной вероятностью и разумной сложностью.

Способность выполнять экономичное декодирование с мягким решением с максимальным правдоподобием является одним из основных преимуществ сверточных кодов. В этом отличие от классических блочных кодов, которые обычно представляются изменяющейся во времени решеткой и поэтому обычно декодируются с жестким решением. Сверточные коды часто характеризуются базовой скоростью кода и глубиной (или памятью) кодера. $[n,k,K]$ . Базовая скорость кода обычно задается как $n/k$ , где $n$ — скорость необработанных входных данных, а $k$ — скорость данных закодированного потока выходного канала. $n$ меньше $k$ , поскольку канальное кодирование вводит избыточность во входные биты. Память часто называют «длиной ограничения» $K$ , где выходной сигнал является функцией текущего ввода, а также предыдущего. $K-1$ входы. Глубина также может быть задана как количество элементов памяти $v$ в полиноме или максимально возможное количество состояний кодера (обычно: $2^{v}$ ).

Сверточные коды часто описываются как непрерывные. Однако можно также сказать, что сверточные коды имеют произвольную длину блока, а не являются непрерывными, поскольку большая часть реального сверточного кодирования выполняется над блоками данных. Блочные коды сверточного кодирования обычно используют завершение. Произвольную длину блока сверточных кодов также можно противопоставить классическим блочным кодам , которые обычно имеют фиксированную длину блока, определяемую алгебраическими свойствами.

Скорость кода сверточного кода обычно модифицируется посредством выкалывания символов . Например, сверточный код с «материнской» скоростью кода. $n/k=1/2$ могут быть проколоты до более высокой скорости, например, $7/8$ просто не передавая часть кодовых символов. Производительность проколотого сверточного кода обычно хорошо масштабируется в зависимости от количества передаваемой четности. Способность выполнять экономичное декодирование с мягким решением на сверточных кодах, а также гибкость сверточных кодов по длине блока и скорости кода делают их очень популярными для цифровой связи.

История

Сверточные коды были введены в 1955 году Питером Элиасом . Считалось, что сверточные коды можно декодировать с произвольным качеством за счет вычислений и задержек. В 1967 году Эндрю Витерби определил, что сверточные коды могут быть декодированы с максимальной вероятностью и разумной сложностью с использованием инвариантных ко времени решетчатых декодеров — алгоритма Витерби . Позже были разработаны другие алгоритмы декодера на основе решетки, включая алгоритм декодирования BCJR .

Рекурсивные систематические сверточные коды были изобретены Клодом Берру примерно в 1991 году. Эти коды оказались особенно полезными для итеративной обработки, включая обработку составных кодов, таких как турбокоды . ^[1]

Используя «сверточную» терминологию, классический сверточный код можно рассматривать как фильтр с конечной импульсной характеристикой (FIR), а рекурсивный сверточный код можно рассматривать как фильтр с бесконечной импульсной характеристикой (IIR).

Где используются сверточные коды

Сверточные коды широко используются для обеспечения надежной передачи данных во многих приложениях, таких как цифровое видео , радио, мобильная связь (например, в сетях GSM, GPRS, EDGE и 3G (до версии 3GPP Release 7). ^[3]^[4]) и спутниковая связь . ^[5] Эти коды часто реализуются в сочетании с кодом жесткого принятия решения, особенно с кодом Рида-Соломона . До появления турбокодов такие конструкции были наиболее эффективными и наиболее близки к пределу Шеннона .

Сверточное кодирование

Для сверточного кодирования данных начните с k регистров памяти , каждый из которых содержит один входной бит. Если не указано иное, все регистры памяти начинаются со значения 0. Кодировщик имеет n по модулю 2 сумматоров (сумматор по модулю 2 может быть реализован с помощью одного логического элемента XOR , где логика: $0+0 = 0$ , $0+ 1 = 1$ , $1+0 = 1$ , $1+1 = 0$ ) и n генераторных полиномов — по одному на каждый сумматор (см. рисунок ниже). Входной бит m ₁ подается в самый левый регистр. Используя полиномы генератора и существующие значения в остальных регистрах, кодер выводит n символов. Эти символы могут передаваться или прокалываться в зависимости от желаемой скорости кода. Теперь побитовый сдвиг всех значений регистра вправо ( m ₁ перемещается в m ₀ , m ₀ перемещается в m ₋₁ ) и дождитесь следующего входного бита. Если оставшихся входных битов нет, кодер продолжает сдвиг до тех пор, пока все регистры не вернутся в нулевое состояние (завершение сброса битов).

Изображение 1. Нерекурсивный несистематический сверточный кодер со скоростью 1/3 и длиной ограничения 3

На рисунке ниже указана ставка 1 ⁄ 3 ( m ⁄ n ) кодер с длиной ограничения ( k ) равной 3. Полиномами генератора являются $G 1 = (1,1,1),$ $G 2 = (0,1,1)$ и $G 3 = (1,0,1)$ . Таким образом, выходные биты вычисляются (по модулю 2) следующим образом:

п ₁ = м ₁ + м ₀ + м _-1

п ₂ = м ₀ + м _-1

п _{3 знак} равно м ₁ + м _-1 .

Сверточные коды могут быть систематическими и несистематическими:

систематическое повторение структуры сообщения перед кодированием
несистематическое изменение исходной структуры

Несистематические сверточные коды более популярны из-за лучшей помехоустойчивости. Это относится к свободному расстоянию сверточного кода. ^[6]

Краткая иллюстрация несистематического сверточного кода.
Краткая иллюстрация систематического сверточного кода.

Рекурсивные и нерекурсивные коды

Кодировщик на рисунке выше является нерекурсивным кодером. Вот пример рекурсивного метода, который допускает структуру обратной связи:

Пример кодера является систематическим , поскольку входные данные также используются в выходных символах (Выход 2). Коды с выходными символами, не включающими в себя входные данные, называются несистематическими.

Рекурсивные коды обычно являются систематическими, и, наоборот, нерекурсивные коды обычно несистематические. Это не строгое требование, а обычная практика.

Пример кодировщика на рис. 2. является энкодером с 8 состояниями, поскольку 3 регистра создают 8 возможных состояний энкодера (2 ³). Соответствующая решетка декодера обычно также использует 8 состояний.

Рекурсивные систематические сверточные коды (RSC) стали более популярными благодаря их использованию в турбокодах. Рекурсивные систематические коды также называются псевдосистематическими кодами.

Другие коды RSC и примеры приложений включают:

Полезно для реализации кода LDPC и в качестве внутреннего составного кода для последовательных составных сверточных кодов (SCCC).

Полезно для SCCC и многомерных турбокодов.

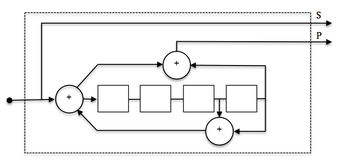
Полезен в качестве составного кода в турбокодах с низкой частотой ошибок для таких приложений, как спутниковые линии связи. Также подходит в качестве внешнего кода SCCC.

Импульсная характеристика, передаточная функция и длина ограничения

Сверточный кодер называется так потому, что он выполняет свертку кодера входного потока с импульсными характеристиками :

y_{i}^{j}=\sum _{k=0}^{\infty }h_{k}^{j}x_{i-k}=(x*h^{j})[i],

где $x$ — входная последовательность, $y дж$ — это последовательность с выхода $j$ , $h дж$ - импульсная характеристика для выхода $j$ и ${*}$ обозначает свертку.

Сверточный кодер — это дискретная линейная стационарная система . Каждый выход кодера может быть описан собственной передаточной функцией , которая тесно связана с полиномом генератора. Импульсная характеристика связана с передаточной функцией посредством Z-преобразования .

Передаточные функции для первого (нерекурсивного) кодера:

$H_{1}(z)=1+z^{-1}+z^{-2},\,$
$H_{2}(z)=z^{-1}+z^{-2},\,$
$H_{3}(z)=1+z^{-2}.\,$

Передаточные функции для второго (рекурсивного) кодера:

$H_{1}(z)={\frac {1+z^{-1}+z^{-3}}{1-z^{-2}-z^{-3}}},\,$
$H_{2}(z)=1.\,$

Определите $m$ по

m=\max _{i}\operatorname {polydeg} (H_{i}(1/z))\,

где для любой рациональной функции $f(z)=P(z)/Q(z)\,$ ,

\operatorname {polydeg} (f)=\max(\deg(P),\deg(Q))\,

.

Тогда $m$ — максимальная из полиномиальных степеней

$H_{i}(1/z)\,$ , а длина ограничения определяется как $K=m+1\,$ . Например, в первом примере длина ограничения равна 3, а во втором — длина ограничения 4.

Схема решетки

Сверточный кодер — это конечный автомат . Кодер с n двоичными ячейками будет иметь 2 ^н государства.

Представьте, что кодер (показанный на рисунке 1 выше) имеет «1» в левой ячейке памяти ( m ₀ ) и «0» в правой ( m ₋₁ ). ( m ₁ на самом деле не является ячейкой памяти, поскольку представляет текущее значение). Обозначим такое состояние как «10». В соответствии с входным битом энкодер на следующем обороте может перейти либо в состояние «01», либо в состояние «11». Видно, что не все переходы возможны (например, декодер не может преобразовать состояние «10» в состояние «00» или даже остаться в состоянии «10»).

Все возможные переходы можно показать, как показано ниже:

Фактическую закодированную последовательность можно представить в виде пути на этом графе. В качестве примера один действительный путь показан красным.

Эта диаграмма дает нам представление о декодировании : если полученная последовательность не укладывается в этот граф, значит, она получена с ошибками, и мы должны выбрать ближайшую правильную (подходящую к графу) последовательность. Настоящие алгоритмы декодирования используют эту идею.

Свободное расстояние и распределение ошибок

Теоретические кривые частоты битовых ошибок закодированной QPSK (рекурсивное и нерекурсивное, мягкое решение), канал аддитивного белого гауссовского шума. Кривые мало выделяются из-за примерно одинаковых свободных расстояний и весов.

Свободная дистанция ^[7] ( d ) — минимальное расстояние Хэмминга между различными кодированными последовательностями. Корректирующая способность ( t ) сверточного кода — это количество ошибок, которые можно исправить с помощью кода. Его можно рассчитать как

t=\left\lfloor {\frac {d-1}{2}}\right\rfloor .

Поскольку сверточный код не использует блоки, а обрабатывает непрерывный битовый поток, значение t применяется к количеству ошибок, расположенных относительно близко друг к другу. То есть несколько групп t ошибок обычно можно исправить, если они находятся относительно далеко друг от друга.

Свободное расстояние можно интерпретировать как минимальную длину ошибочного «пакета» на выходе сверточного декодера. Тот факт, что ошибки появляются как «пакеты», следует учитывать при разработке составного кода с внутренним сверточным кодом. Популярным решением этой проблемы является чередование данных перед сверточным кодированием, чтобы код внешнего блока (обычно Рида-Соломона ) мог исправить большинство ошибок.

Декодирование сверточных кодов

Существует несколько алгоритмов декодирования сверточных кодов. Для относительно небольших значений k алгоритм Витерби используется повсеместно, поскольку он обеспечивает максимальную производительность правдоподобия и легко распараллеливается. Таким образом, декодеры Витерби легко реализовать в аппаратном обеспечении СБИС и в программном обеспечении процессоров с наборами инструкций SIMD .

Коды с большей длиной ограничения более практично декодируются с помощью любого из нескольких алгоритмов последовательного декодирования , из которых Фано наиболее известен алгоритм . В отличие от декодирования Витерби, последовательное декодирование не является методом максимального правдоподобия, но его сложность увеличивается лишь незначительно с увеличением длины ограничения, что позволяет использовать сильные коды с большой длиной ограничения. Такие коды использовались в программе «Пионер» в начале 1970-х годов для Юпитера и Сатурна, но уступили место более коротким кодам, декодированным по Витерби, обычно объединенным с большими кодами исправления ошибок Рида – Соломона , которые увеличивают общую кривую частоты ошибок по битам и создают чрезвычайно низкий уровень остаточных необнаруженных ошибок.

И алгоритмы Витерби, и алгоритмы последовательного декодирования возвращают трудные решения: биты, которые образуют наиболее вероятное кодовое слово. К каждому биту можно добавить приблизительную меру достоверности с помощью алгоритма Витерби с мягким выходом . Максимально апостериорные (MAP) мягкие решения для каждого бита можно получить с помощью алгоритма BCJR .

Перфорированные сверточные коды

Сверточные коды со скоростями кодирования 1/2 и 3/4 (и длиной ограничения 7, мягкое решение, 4-QAM/QPSK/OQPSK). ^[14]

Сверточный код с любой скоростью кода может быть разработан на основе полиномиального выбора; ^[15] однако на практике для достижения требуемой скорости кода часто используется процедура прокалывания. Прокалывание — это метод, используемый для создания кода скорости m / n из «базового» низкоскоростного (например, 1/ n ) кода. Это достигается удалением некоторых битов на выходе кодера. Биты удаляются в соответствии с матрицей выкалывания . Наиболее часто используются следующие матрицы выкалывания:

Скорость кода

Матрица прокалывания

Свободное расстояние (для стандартного сверточного кода НАСА K=7)

1/2
(Без перф.)

1

10

2/3

1	0
1	1

6

3/4

1	0	1
1	1	0

5

5/6

1	0	1	0	1
1	1	0	1	0

4

7/8

1	0	0	0	1	0	1
1	1	1	1	0	1	0

3

Например, если мы хотим создать код со скоростью 2/3, используя соответствующую матрицу из приведенной выше таблицы, мы должны взять выход базового кодера и передать каждый первый бит из первой ветви и каждый бит из второй. Конкретный порядок передачи определяется соответствующим стандартом связи.

Проколотые сверточные коды широко используются в спутниковой связи , например, в системах Intelsat и цифрового видеовещания .

Перфорированные сверточные коды также называют «перфорированными».

Турбокоды: замена сверточных кодов

Простые сверточные коды, декодируемые Витерби, теперь уступают место турбокодам , новому классу итерированных коротких сверточных кодов, которые близко приближаются к теоретическим ограничениям, налагаемым теоремой Шеннона, с гораздо меньшей сложностью декодирования, чем алгоритм Витерби для длинных сверточных кодов, которые потребуются. за ту же производительность. Конкатенация с внешним алгебраическим кодом (например, Рида-Соломона ) решает проблему минимального уровня ошибок, свойственную конструкциям турбокодов.

См. также

Квантовый сверточный код

Ссылки

В этой статье использованы общедоступные материалы из Федеральный стандарт 1037C . Управление общего обслуживания . Архивировано из оригинала 22 января 2022 г.

^ Бенедетто, Серджио и Гвидо Монторси. « Роль рекурсивных сверточных кодов в турбокодах ». Electronics Letters 31.11 (1995): 858-859.
^ Эберспехер Дж. и др. GSM-архитектура, протоколы и сервисы. Джон Уайли и сыновья, 2008. стр.97.
^ Проект партнерства 3-го поколения (сентябрь 2012 г.). «3GGP TS45.001: Группа технических спецификаций Сеть радиодоступа GSM/EDGE; Физический уровень на радиотракте; Общее описание». Проверено 20 июля 2013 г.
^ Халонен, Тимо, Хавьер Ромеро и Хуан Мелеро, ред. Производительность GSM, GPRS и EDGE: эволюция в сторону 3G/UMTS. Джон Уайли и сыновья, 2004. с. 430
^ Бутман, С.А., LJ Deutsch и RL Miller. «Выполнение составных кодов для полетов в дальний космос». Отчет о ходе работы в области телекоммуникаций и сбора данных 42–63, март – апрель 1981 г. (1981): 33–39.
^ Мун, Тодд К. «Кодирование с коррекцией ошибок». Математические методы и алгоритмы. Джон Уайли и сын (2005). п. 508
^ Мун, Тодд К. « Кодирование с коррекцией ошибок ». Математические методы и алгоритмы. Джон Уайли и сын (2005).- стр.508.
^ LLR против демодуляции жесткого решения (MathWorks)
^ Оценка BER для декодирования Витерби с жестким и мягким решением (MathWorks)
^ Цифровая модуляция: точный алгоритм LLR (MathWorks)
^ Цифровая модуляция: приблизительный алгоритм LLR (MathWorks)
^ Бутман, С.А., LJ Deutsch и RL Miller. «Выполнение составных кодов для полетов в дальний космос». Отчет о ходе работы в области телекоммуникаций и сбора данных 42–63, март – апрель 1981 г. (1981): 33–39.
^ Глобальная система мобильной связи (GSM)
^ Проколотое сверточное кодирование (MathWorks)
^ «Преобразуйте полиномы сверточного кода в описание решетки – MATLAB poly2trellis» .
^ Турбо-код
^ Бенедетто, Серджио и Гвидо Монторси. « Роль рекурсивных сверточных кодов в турбокодах ». Electronics Letters 31.11 (1995): 858-859.

Внешние ссылки

В онлайн-учебнике Теория информации, вывод и алгоритмы обучения » Дэвида Дж. Маккея « сверточные коды обсуждаются в главе 48.
Страница кодов исправления ошибок (ECC)
Пояснения к Матлабу
Основы сверточных декодеров для улучшения цифровых коммуникаций
Сверточные коды (MIT)
Теория информации и кодирование (TU Ilmenau). Архивировано 30 августа 2017 г. в Wayback Machine , на странице 48 обсуждаются сверточные коды.

Дальнейшее чтение

Публикации

Фрэнсис, Майкл. «Блочное декодирование декодера Витерби — завершение решетки и закрепление хвоста». Xilinx XAPP551 v2. 0, ДД (2005): 1-21.
Чен, Цинчунь, Вай Хо Моу и Пинчжи Фань. «Некоторые новые результаты по рекурсивным сверточным кодам и их приложениям». Семинар по теории информации, 2006. ITW'06, Чэнду. IEEE. ИИЭР, 2006.
Фибиг, Калифорнийский университет, и Патрик Робертсон. «Мягкое решение и декодирование со стиранием в системах с быстрой перестройкой частоты со сверточными, турбо-кодами и кодами Рида-Соломона». Транзакции IEEE по коммуникациям 47.11 (1999): 1646-1654.
Бхаскар, Видьячаран и Лори Л. Джойнер. «Производительность проколотых сверточных кодов в асинхронной связи CDMA в идеальных условиях отслеживания фазы». Компьютеры и электротехника 30.8 (2004): 573-592.
Модестино Дж. и Шоу Муи. «Производительность сверточного кода в канале затухания Райса». Транзакции IEEE по коммуникациям 24.6 (1976): 592-606.
Чен, Ю-Лонг и Че-Хо Вэй. «Оценка производительности сверточных кодов с MPSK на каналах с затуханием Райса». Слушания IEE F-коммуникации, радар и обработка сигналов. Том. 134. № 2. ИЭПП, 1987.

[1] Бенедетто, Серджио и Гвидо Монторси. « Роль рекурсивных сверточных кодов в турбокодах ». Electronics Letters 31.11 (1995): 858-859.

[2] Эберспехер Дж. и др. GSM-архитектура, протоколы и сервисы. Джон Уайли и сыновья, 2008. стр.97.

[3] Проект партнерства 3-го поколения (сентябрь 2012 г.). «3GGP TS45.001: Группа технических спецификаций Сеть радиодоступа GSM/EDGE; Физический уровень на радиотракте; Общее описание». Проверено 20 июля 2013 г.

[4] Халонен, Тимо, Хавьер Ромеро и Хуан Мелеро, ред. Производительность GSM, GPRS и EDGE: эволюция в сторону 3G/UMTS. Джон Уайли и сыновья, 2004. с. 430

[5] Бутман, С.А., LJ Deutsch и RL Miller. «Выполнение составных кодов для полетов в дальний космос». Отчет о ходе работы в области телекоммуникаций и сбора данных 42–63, март – апрель 1981 г. (1981): 33–39.

[6] Мун, Тодд К. «Кодирование с коррекцией ошибок». Математические методы и алгоритмы. Джон Уайли и сын (2005). п. 508

[7] Мун, Тодд К. « Кодирование с коррекцией ошибок ». Математические методы и алгоритмы. Джон Уайли и сын (2005).- стр.508.

[8] LLR против демодуляции жесткого решения (MathWorks)

[9] Оценка BER для декодирования Витерби с жестким и мягким решением (MathWorks)

[10] Цифровая модуляция: точный алгоритм LLR (MathWorks)

[11] Цифровая модуляция: приблизительный алгоритм LLR (MathWorks)

[12] Бутман, С.А., LJ Deutsch и RL Miller. «Выполнение составных кодов для полетов в дальний космос». Отчет о ходе работы в области телекоммуникаций и сбора данных 42–63, март – апрель 1981 г. (1981): 33–39.

[13] Глобальная система мобильной связи (GSM)

[14] Проколотое сверточное кодирование (MathWorks)

[15] «Преобразуйте полиномы сверточного кода в описание решетки – MATLAB poly2trellis» .

[16] Турбо-код

[17] Бенедетто, Серджио и Гвидо Монторси. « Роль рекурсивных сверточных кодов в турбокодах ». Electronics Letters 31.11 (1995): 858-859.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]