метод Ромберга

Эта статья о методе численного интегрирования. Информацию о приеме неврологического обследования см. в тесте Ромберга .

В численном анализе метод Ромберга используется для оценки определенного интеграла $$\int _{a}^{b}f(x)\,dx$$ применив экстраполяцию Ричардсона неоднократно по правилу трапеции или правилу прямоугольника (правилу средней точки). Оценки создают треугольный массив . Метод Ромберга представляет собой формулу Ньютона-Котеса : он оценивает подынтегральную функцию в равноотстоящих друг от друга точках. Подынтегральная функция должна иметь непрерывные производные, хотя и достаточно хорошие результаты. можно получить, если существует лишь несколько производных. Если подынтегральное выражение можно вычислить в неравноотстоящих точках, то другие методы, такие как квадратура Гаусса и квадратура Кленшоу – Кертиса, обычно более точны.

Метод назван в честь Вернера Ромберга , опубликовавшего метод в 1955 году.

Метод

С использованием ${\textstyle h_{n}={\frac {(b-a)}{2^{n}}}}$, метод можно определить индуктивно по формуле $${\begin{aligned}R(0,0)&=h_{1}(f(a)+f(b))\\R(n,0)&={\tfrac {1}{2}}R(n-1,0)+h_{n}\sum _{k=1}^{2^{n-1}}f(a+(2k-1)h_{n})\\R(n,m)&=R(n,m-1)+{\tfrac {1}{4^{m}-1}}(R(n,m-1)-R(n-1,m-1))\\&={\frac {1}{4^{m}-1}}(4^{m}R(n,m-1)-R(n-1,m-1))\end{aligned}}$$ где $n\geq m$ и $m\geq 1\,$. В обозначении большого O ошибка для R ( n , m ) равна: $O\left(h_{n}^{2m+2}\right).$

Нулевая экстраполяция R ( n , 0) эквивалентна правилу трапеций с 2 ^н + 1 балл; первая экстраполяция R ( n , 1) эквивалентна правилу Симпсона с 2 ^н + 1 балл. Вторая экстраполяция, R ( n , 2) , эквивалентна правилу Буля с 2 ^н + 1 балл. Дальнейшие экстраполяции отличаются от формул Ньютона-Котеса. В частности, дальнейшие экстраполяции Ромберга очень незначительно расширяют правило Буля, изменяя веса в соотношения, аналогичные тем, что есть в правиле Буля. Напротив, дальнейшие методы Ньютона-Котеса дают все более различающиеся веса, что в конечном итоге приводит к большим положительным и отрицательным весам. Это свидетельствует о том, что методы Ньютона-Котеса с интерполяционным полиномом большой степени не сходятся для многих интегралов, в то время как интегрирование Ромберга более стабильно.

Маркируя наши ${\textstyle O(h^{2})}$ приближения как ${\textstyle A_{0}{\big (}{\frac {h}{2^{n}}}{\big )}}$ вместо ${\textstyle R(n,0)}$, мы можем выполнить экстраполяцию Ричардсона с помощью формулы ошибки, определенной ниже: $$\int _{a}^{b}f(x)\,dx=A_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}+a_{0}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{2}+a_{1}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{4}+a_{2}{\bigg (}{\frac {h}{2^{n}}}{\bigg )}^{6}+\cdots$$ Как только мы получили наши ${\textstyle O(h^{2(m+1)})}$ приближения ${\textstyle A_{m}{\big (}{\frac {h}{2^{n}}}{\big )}}$, мы можем обозначить их как ${\textstyle R(n,m)}$.

Когда оценки функций являются дорогостоящими, может быть предпочтительнее заменить полиномиальную интерполяцию Ричардсона рациональной интерполяцией, предложенной Bulirsch & Stoer (1967) .

Геометрический пример

Для оценки площади под кривой правило трапеций применяется сначала к одной детали, затем к двум, затем к четырем и так далее.

Один кусочек. Обратите внимание: поскольку оно начинается и заканчивается в нуле, это приближение дает нулевую площадь.

Двухсекционный

Четырехчастный

Восьмисекционный

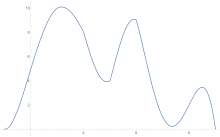
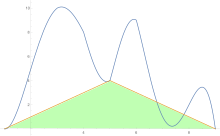
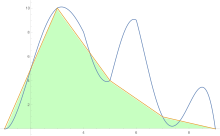
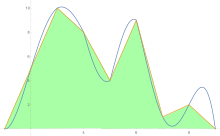
После получения оценок по правилу трапеций экстраполяция Ричардсона применяется .

• Для первой итерации в формуле используются двухштучные и одноштучные оценки ⁠ 4 × (более точно) − (менее точно) / 3 ⁠ . Затем та же формула используется для сравнения сметы из четырех и двух частей, а также для более высоких оценок.
• Для второй итерации в формуле используются значения первой итерации ⁠ 16 × (более точно) − (менее точно) / 15 ⁠
• Третья итерация использует следующую степень 4: ⁠ 64 × (более точно) − (менее точно) / 63 ⁠ от значений, полученных во второй итерации.
• Шаблон продолжается до тех пор, пока не останется одна оценка.

Количество штук	Оценки трапеции	Первая итерация	Вторая итерация	Третья итерация
		⁠ 4 МА − А / 3 ⁠	⁠ 16 МА − А / 15 ⁠	⁠ 64 МА − А / 63 ⁠
1	0	⁠ 4×16 − 0 / 3 ⁠ = 21.333...	⁠ 16×34.667 − 21.333 / 15 ⁠ = 35.556...	⁠ 64×42.489 − 35.556 / 63 ⁠ = 42.599...
2	16	⁠ 4×30 − 16 / 3 ⁠ = 34.666...	⁠ 16×42 − 34.667 / 15 ⁠ = 42.489...
4	30	⁠ 4×39 − 30 / 3 ⁠ = 42
8	39

Пример

Например, функция Гаусса интегрируется от 0 до 1, т.е. функция ошибок erf(1) ≈ 0,842700792949715. Треугольный массив вычисляется построчно и расчет прекращается, если две последние записи в последней строке отличаются менее чем на 10. ⁻⁸ .

0.77174333
0.82526296  0.84310283
0.83836778  0.84273605  0.84271160
0.84161922  0.84270304  0.84270083  0.84270066
0.84243051  0.84270093  0.84270079  0.84270079  0.84270079

Результат в правом нижнем углу треугольного массива соответствует показанным цифрам. Примечательно, что этот результат получен на основе менее точных приближений полученное по правилу трапеций в первом столбце треугольного массива.

Выполнение

Вот пример компьютерной реализации метода Ромберга (на языке программирования Си ):

#include <stdio.h>
#include <math.h>

void print_row(size_t i, double *R) {
  printf("R[%2zu] = ", i);
  for (size_t j = 0; j <= i; ++j) {
    printf("%f ", R[j]);
  }
  printf("\n");
}

/*
INPUT:
(*f) : pointer to the function to be integrated
a    : lower limit
b    : upper limit
max_steps: maximum steps of the procedure
acc  : desired accuracy

OUTPUT:
Rp[max_steps-1]: approximate value of the integral of the function f for x in [a,b] with accuracy 'acc' and steps 'max_steps'.
*/
double romberg(double (*f)(double), double a, double b, size_t max_steps, double acc) 
{
  double R1[max_steps], R2[max_steps]; // buffers
  double *Rp = &R1[0], *Rc = &R2[0]; // Rp is previous row, Rc is current row
  double h = b-a; //step size
  Rp[0] = (f(a) + f(b))*h*0.5; // first trapezoidal step

  print_row(0, Rp);

  for (size_t i = 1; i < max_steps; ++i) {
    h /= 2.;
    double c = 0;
    size_t ep = 1 << (i-1); //2^(n-1)
    for (size_t j = 1; j <= ep; ++j) {
      c += f(a + (2*j-1) * h);
    }
    Rc[0] = h*c + .5*Rp[0]; // R(i,0)

    for (size_t j = 1; j <= i; ++j) {
      double n_k = pow(4, j);
      Rc[j] = (n_k*Rc[j-1] - Rp[j-1]) / (n_k-1); // compute R(i,j)
    }

    // Print ith row of R, R[i,i] is the best estimate so far
    print_row(i, Rc);

    if (i > 1 && fabs(Rp[i-1]-Rc[i]) < acc) {
      return Rc[i];
    }

    // swap Rn and Rc as we only need the last row
    double *rt = Rp;
    Rp = Rc;
    Rc = rt;
  }
  return Rp[max_steps-1]; // return our best guess
}

Вот реализация метода Ромберга (на языке программирования Python ):

def print_row(i, R):
  """Prints a row of the Romberg table."""
  print(f"R[{i:2d}] = ", end="")
  for j in range(i + 1):
    print(f"{R[j]:f} ", end="")
  print()

def romberg(f, a, b, max_steps, acc):
  """
  Calculates the integral of a function using Romberg integration.

  Args:
      f: The function to integrate.
      a: Lower limit of integration.
      b: Upper limit of integration.
      max_steps: Maximum number of steps.
      acc: Desired accuracy.

  Returns:
      The approximate value of the integral.
  """
  R1, R2 = [0] * max_steps, [0] * max_steps  # Buffers for storing rows
  Rp, Rc = R1, R2  # Pointers to previous and current rows

  h = b - a  # Step size
  Rp[0] = 0.5 * h * (f(a) + f(b))  # First trapezoidal step

  print_row(0, Rp)

  for i in range(1, max_steps):
    h /= 2.
    c = 0
    ep = 1 << (i - 1)  # 2^(i-1)
    for j in range(1, ep + 1):
      c += f(a + (2 * j - 1) * h)
    Rc[0] = h * c + 0.5 * Rp[0]  # R(i,0)

    for j in range(1, i + 1):
      n_k = 4**j
      Rc[j] = (n_k * Rc[j - 1] - Rp[j - 1]) / (n_k - 1)  # Compute R(i,j)

    # Print ith row of R, R[i,i] is the best estimate so far
    print_row(i, Rc)

    if i > 1 and abs(Rp[i - 1] - Rc[i]) < acc:
      return Rc[i]

    # Swap Rn and Rc for next iteration
    Rp, Rc = Rc, Rp

  return Rp[max_steps - 1]  # Return our best guess

Ссылки

Библиография

• Ричардсон, LF (1911), «Приблизительное арифметическое решение с помощью конечных разностей физических задач, включающих дифференциальные уравнения, с применением к напряжениям в каменной плотине», Philosophical Transactions of the Royal Society A , 210 (459–470): 307 –357, номер домена : 10.1098/rsta.1911.0009 , JSTOR   90994.
• Ромберг, В. (1955), «Vereinfachte numerische Integration», Труды Королевского норвежского общества наук , 28 (7), Тронхейм: 30–36.
• Тэчер-младший, Генри К. (июль 1964 г.), «Замечание об алгоритме 60: интеграция Ромберга» , Communications of ACM , 7 (7): 420–421, doi : 10.1145/364520.364542
• Бауэр, Флорида; Рутисхаузер, Х.; Стифель, Э. (1963), Метрополис, Северная Каролина; и др. (ред.), «Новые аспекты числовой квадратуры», Экспериментальная арифметика, высокоскоростные вычисления и математика, Труды симпозиумов по прикладной математике (15), AMS : 199–218
• Булирш, Роланд; Стер, Йозеф (1967), «Справочник по численному интегрированию. Числовая квадратура путем экстраполяции» , Numerische Mathematics , 9 : 271–278, doi : 10.1007/bf02162420
• Мысовских, ИП (2002) [1994], «Метод Ромберга» , в Хазевинкеле, Михиэле (ред.), Энциклопедия математики , Springer-Verlag , ISBN  1-4020-0609-8
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 4.3. Интеграция Ромберга» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN  978-0-521-88068-8

Внешние ссылки

• ROMBINT – код для MATLAB (автор: Мартин Каченак)
• Бесплатный онлайн-инструмент интеграции с использованием Ромберга, Фокса-Ромберга, Гаусса-Лежандра и других численных методов.
• SciPy реализация метода Ромберга
• Romberg.jl — реализация Julia (поддержка произвольных факторизаций, а не только $2^{n}+1$ баллы)