Тяжелый фермионный материал

В материаловедении тяжелые фермионные материалы представляют собой особый тип интерметаллических соединений , содержащих элементы с 4f или 5f электронами в незаполненных электронных зонах . Электроны — это один из типов фермионов , и когда они обнаруживаются в таких материалах, их иногда называют тяжелыми электронами . Тяжелые фермионные материалы обладают низкотемпературной удельной теплоемкостью , линейный член которой до 1000 раз превышает значение, ожидаемое из модели свободных электронов . Свойства соединений тяжелых фермионов часто обусловлены частично заполненными f-орбиталями редкоземельных или актинидных ионов , которые ведут себя как локализованные магнитные моменты .

Название «тяжелый фермион» происходит от того факта, что фермион ведет себя так, как если бы его эффективная масса превышала его массу покоя. В случае электронов при температуре ниже характеристической температуры (обычно 10 К) электроны проводимости в этих металлических соединениях ведут себя так, как если бы их эффективная масса в 1000 раз превышала массу свободных частиц . Эта большая эффективная масса также отражается в большом вкладе в удельное сопротивление рассеяния электронов через соотношение Кадоваки-Вудса . Поведение тяжелых фермионов было обнаружено в самых разных состояниях, включая металлические, сверхпроводящие , изолирующие и магнитные состояния. Характерными примерами являются CeCu ₆ , CeAl ₃ , CeCu ₂ Si ₂ , YbAl ₃ , UBe ₁₃ и UPt ₃ .

Исторический обзор

Поведение тяжелых фермионов было обнаружено К. Андресом, Дж. Э. Гребнером и Х. Р. Оттом в 1975 году, которые наблюдали огромные величины линейной удельной теплоемкости в CeAl ₃ .

В то время как исследования легированных сверхпроводников привели к выводу о несовместимости существования локализованных магнитных моментов и сверхпроводимости в одном материале, было показано обратное, когда в 1979 году Франк Стеглих и др. обнаружил сверхпроводимость тяжелых фермионов в материале CeCu ₂ Si ₂ .

В 1994 году открытие квантовой критической точки и нефермижидкостного поведения на фазовой диаграмме соединений тяжелых фермионов Х. фон Лёнейсеном и др. привело к новому подъему интереса к исследованию этих соединений. Другим экспериментальным прорывом стала демонстрация в 1998 году (группой Джила Лонзарича ), что квантовая критичность тяжелых фермионов может быть причиной нетрадиционной сверхпроводимости.

Тяжелые фермионные материалы играют важную роль в текущих научных исследованиях, выступая в качестве прототипов материалов для нетрадиционной сверхпроводимости , поведения неферми-жидкости и квантовой критичности. Фактическое взаимодействие между локализованными магнитными моментами и электронами проводимости в соединениях тяжелых фермионов до сих пор полностью не изучено и является темой продолжающихся исследований.

Характеристики

Тяжелые фермионные материалы относятся к группе сильно коррелированных электронных систем .

Некоторые члены группы тяжелых фермионных материалов становятся сверхпроводящими при температуре ниже критической. Сверхпроводимость является нетрадиционной , т.е. не охваченной теорией БКШ .

При высоких температурах соединения тяжелых фермионов ведут себя как обычные металлы, а электроны можно описать как ферми-газ , в котором электроны считаются невзаимодействующими фермионами. В этом случае взаимодействием между f -электронами, представляющими локальный магнитный момент, и электронами проводимости можно пренебречь.

Теория ферми-жидкости Льва Ландау обеспечивает хорошую модель для описания свойств большинства тяжелых фермионных материалов при низких температурах. В этой теории электроны описываются квазичастицами , имеющими одинаковые квантовые числа и заряд, но взаимодействие электронов учитывается введением эффективной массы , отличающейся от фактической массы свободного электрона.

Оптические свойства

Типичная частотно-зависимая оптическая проводимость тяжелого фермионного соединения. Синяя линия: T > T _coh . Красная линия: T < T _coh .

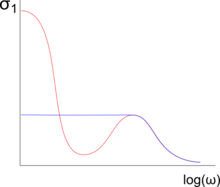
Чтобы получить оптические свойства тяжелых фермионных систем, эти материалы были исследованы с помощью оптической спектроскопии . В этих экспериментах образец облучается электромагнитными волнами с перестраиваемой длиной волны . Измерение отраженного или прошедшего света позволяет выявить характеристические энергии образца.

Выше характеристической температуры когерентности $T_{\rm {coh}}$, тяжелые фермионные материалы ведут себя как обычные металлы; т.е. их оптический отклик описывается моделью Друде . Однако по сравнению с хорошим металлом соединения тяжелых фермионов при высоких температурах имеют высокую скорость рассеяния из-за большой плотности локальных магнитных моментов (по крайней мере, один f-электрон на элементарную ячейку), которые вызывают (некогерентное) Кондо -рассеяние. Из-за высокой скорости рассеяния проводимость на постоянном токе и на низких частотах довольно мала. Спад проводимости (спад Друде) происходит на частоте, соответствующей скорости релаксации.

Ниже $T_{\rm {coh}}$, локализованные f -электроны гибридизуются с электронами проводимости. Это приводит к увеличению эффективной массы и развитию гибридизационного разрыва. В отличие от изоляторов Кондо , химический потенциал соединений тяжелых фермионов лежит внутри зоны проводимости. Эти изменения приводят к двум важным особенностям оптического отклика тяжелых фермионов.

Зависимая от частоты проводимость материалов с тяжелыми фермионами может быть выражена выражением $\sigma (\omega )={\frac {ne^{2}}{m^{*}}}{\frac {\tau ^{*}}{1+\omega ^{2}\tau ^{*2}}}$, содержащий эффективную массу $m^{*}$ и перенормированная скорость релаксации ${\frac {1}{\tau ^{*}}}={\frac {m}{m^{*}}}{\frac {1}{\tau }}$. Из-за большой эффективной массы также увеличивается перенормированное время релаксации, что приводит к узкому спаду Друде на очень низких частотах по сравнению с обычными металлами. Самая низкая такая скорость друдевской релаксации, наблюдаемая до сих пор в тяжелых фермионах, в диапазоне низких ГГц , была обнаружена в UPd ₂ Al ₃ .

Щелеобразная особенность оптической проводимости представляет собой непосредственно гибридизационную щель, открывающуюся в результате взаимодействия локализованных f-электронов и электронов проводимости. Поскольку проводимость не исчезает полностью, наблюдаемая щель фактически является псевдощелью . На еще более высоких частотах мы можем наблюдать локальный максимум оптической проводимости, обусловленный нормальными межзонными возбуждениями.

Теплоемкость

Удельная теплоемкость обычных металлов

При низкой температуре и для обычных металлов удельная теплоемкость $C_{P}$ состоит из удельной теплоемкости электронов $C_{P,{\rm {el}}}$ которая линейно зависит от температуры $T$ и удельной теплоемкости колебаний кристаллической решетки ( фононов ) $C_{P,{\rm {ph}}}$ которая кубически зависит от температуры

$C_{P}=C_{P,{\rm {el}}}+C_{P,{\rm {ph}}}=\gamma T+\beta T^{3}\$

с константами пропорциональности $\beta$ и $\gamma$.

В указанном выше температурном диапазоне электронный вклад составляет основную часть теплоемкости. В модели свободных электронов — простой модельной системе, в которой не учитывается взаимодействие электронов, — или в металлах, которые можно с ее помощью описать, электронная теплоемкость определяется выражением

$C_{P,{\rm {el}}}=\gamma T={\frac {\pi ^{2}}{2}}{\frac {k_{\rm {B}}}{\epsilon _{\rm {F}}}}nk_{\rm {B}}T$

с постоянной Больцмана $k_{\rm {B}}$, плотность электронов $n$ и энергия Ферми $\epsilon _{\rm {F}}$ (наивысшая энергия одиночной частицы занятых электронных состояний). Константа пропорциональности $\gamma$ называется коэффициентом Зоммерфельда.

Связь между теплоемкостью и «тепловой эффективной массой»

Для электронов с квадратичным законом дисперсии (как и для газа свободных электронов) энергия Ферми ε _F обратно пропорциональна массе частицы m :

$\epsilon _{\rm {F}}={\frac {\hbar ^{2}k_{\rm {F}}^{2}}{2m}}$

где $k_{\rm {F}}$ обозначает волновое число Ферми, которое зависит от плотности электронов и представляет собой абсолютное значение волнового числа самого высокого занятого электронного состояния. Таким образом, поскольку параметр Зоммерфельда $\gamma$ обратно пропорциональна $\epsilon _{\rm {F}}$, $\gamma$ пропорциональна массе частицы и при высоких значениях $\gamma$, металл ведет себя как ферми-газ, в котором электроны проводимости имеют высокую термическую эффективную массу.

Пример: UBe ₁₃ при низких температурах.

Экспериментальные результаты по теплоемкости тяжелого фермионного соединения UBe ₁₃ показывают пик при температуре около 0,75 К, который снижается до нуля с большим наклоном, если температура приближается к 0 К. Из-за этого пика $\gamma$ в этом температурном диапазоне значительно выше, чем в модели свободных электронов. Напротив, выше 6 К удельная теплоемкость этого тяжелого фермионного соединения приближается к значению, ожидаемому из теории свободных электронов.

Квантовая критичность

Наличие локального момента и делокализованных электронов проводимости приводит к конкуренции взаимодействия Кондо (которое благоприятствует немагнитному основному состоянию) и взаимодействия РККИ (которое генерирует магнитоупорядоченные состояния, обычно антиферромагнитные для тяжелых фермионов). Подавив температуру Нееля антиферромагнетика с тяжелыми фермионами до нуля (например, путем приложения давления или магнитного поля или путем изменения состава материала), квантовый фазовый переход . можно вызвать Для нескольких материалов с тяжелыми фермионами было показано, что такой квантовый фазовый переход может генерировать очень выраженные свойства неферми-жидкости при конечных температурах. Такое квантово-критическое поведение также очень подробно изучается в контексте нетрадиционной сверхпроводимости .

Примерами тяжелофермионных материалов с хорошо изученными квантово-критическими свойствами являются CeCu _6−x Au, ЦеИн ₃ , CePd ₂ Si ₂ , YbRh ₂ Si ₂ и CeCoIn ₅ .

Некоторые тяжелые фермионные соединения

• ЦеКоИн ₅
• УРу ₂ Си ₂
• УПД ₂ Аль ₃
• YbBiPt

Дальнейшее чтение

• Киттель, Чарльз (1996) Введение в физику твердого тела , 7-е изд., John Wiley and Sons, Inc.
• Мардер, член парламента (2000), Физика конденсированного состояния, John Wiley & Sons, Нью-Йорк.
• Хьюсон, AC (1993), Проблема Кондо для тяжелых фермионов, Cambridge University Press.
• Фульде П. (1995), Электронные корреляции в молекулах и твердых телах, Springer, Берлин.
• Амуся М., Попов К., Шагинян В., Стефанович В. (2015). Теория соединений тяжелых фермионов - Теория сильно коррелированных ферми-систем . Серия Спрингера по наукам о твердом теле. Том. 182. Спрингер. Бибкод : 2015thct.book.....A . дои : 10.1007/978-3-319-10825-4 . ISBN  978-3-319-10824-7 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )