Большой диснуб диромбидодекаэдр
| Большой диснуб диромбидодекаэдр | |
|---|---|
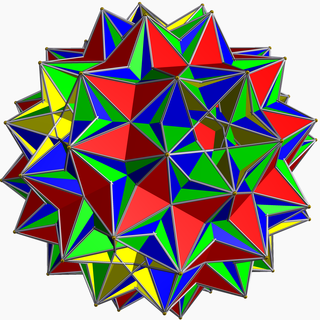 | |
| Тип | Однородный звездчатый многогранник |
| Элементы | Ф = 204, Е = 360 V = 60 (χ = −96) |
| Лица по сторонам | 120{3}+60{4}+24{5/2} |
| Диаграмма Кокстера | {{{Скиллинг-Коксетер}}} |
| Символ Витхоффа | | (3/2) 5/3 (3) 5/2 |
| Группа симметрии | I h , [5,3], *532 |
| Ссылки на индексы | У - , С - , Ш - |
| Двойной многогранник | Большой диснуб диромбидодекакрон |
| Вершинная фигура |  (5/2.4.3.3.3.4. 5/3.4.3/2.3/2.3/2.4)/ 2 |
| Аббревиатура Бауэрса | Гидисдрид |

В геометрии большой диснубированный диромбидодекаэдр , также называемый фигурой Скиллинга , представляет собой вырожденный однородный звездчатый многогранник .
В 1970 году было доказано, что существует только 75 однородных многогранников, кроме бесконечных семейств призм и антипризм . Джон Скиллинг открыл еще один вырожденный пример — великий диснубированный диромбидодекаэдр, ослабив условие, согласно которому ребра должны быть одинарными. Точнее, он позволял любому четному количеству граней встречаться на каждом ребре при условии, что набор граней нельзя было разделить на два связанных набора (Skilling, 1975). Из-за того, что его геометрическая реализация имеет несколько двойных ребер в местах пересечения четырех граней, он считается вырожденным однородным многогранником, но не строго однородным многогранником.
Число ребер неоднозначно, поскольку лежащий в основе абстрактный многогранник имеет 360 ребер, но 120 пар из них имеют одно и то же изображение в геометрической реализации, так что геометрическая реализация имеет 120 одиночных ребер и 120 двойных ребер, где встречаются 4 грани, для всего 240 ребер. Эйлерова характеристика абстрактного многогранника равна −96. Если пары совпадающих ребер в геометрической реализации считать одиночными, то в ней всего 240 ребер и эйлерова характеристика 24.
Вершинная фигура имеет 4 квадратных грани, проходящих через центр модели.
Он может быть построен как комбинация или (смесь) большого диромбикосододекаэдра и соединения двадцати октаэдров .
Связанные многогранники
[ редактировать ]Он имеет то же расположение ребер, что и большой диромбикосидодекаэдр , но имеет другой набор треугольных граней. Вершины и ребра также общие с однородными соединениями двадцати октаэдров или двадцати тетрагемигексаэдров . 180 ребер являются общими с большим курносым додецикосододекаэдром .
 Выпуклая оболочка |  Большой курносый додецикосододекаэдр |  Большой диромбикосидодекаэдр |
 Большой диснуб диромбидодекаэдр |  Соединение двадцати октаэдров |  Соединение двадцати тетрагемигексаэдров. |
Двойной многогранник
[ редактировать ]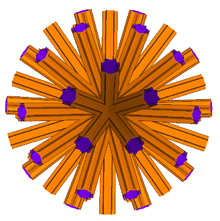
Двойник диснубированного большого диромбидодекаэдра называется большим диснубированным диромбидодекакроном . Это невыпуклый бесконечный равногранный многогранник .
Подобно визуально идентичному большому диромбикосидодекакрону в Магнуса Веннингера » «Двойных моделях , он представлен пересекающимися бесконечными призмами, проходящими через центр модели, срезанными в определенной точке, удобной для создателя. Веннингер предположил, что эти фигуры являются членами нового класса звёздчатых многогранников, названного звёздчатостью до бесконечности . Однако он также признал, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.
Галерея
[ редактировать ] Традиционная начинка | 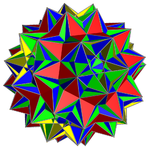 Заполнение по модулю-2 |
См. также
[ редактировать ]Ссылки
[ редактировать ]- Скиллинг, Джон (1975), «Полный набор однородных многогранников», Philosophical Transactions of the Royal Society A , 278 (1278): 111–135, doi : 10.1098/rsta.1975.0022 .
- Вайсштейн, Эрик В. «Большой диромбикосододекаэдр» . Математический мир .
- http://www.software3d.com/MillersMonster.php