Массовый баланс

В физике баланс масс , также называемый материальным балансом , представляет собой применение закона сохранения массы. ^[1] к анализу физических систем . Путем учета материалов, поступающих и выходящих из системы, можно определить массовые потоки , которые могли быть неизвестны или которые было бы трудно измерить без этого метода. Точный закон сохранения, используемый при анализе системы, зависит от контекста проблемы, но все они вращаются вокруг сохранения массы, то есть того, что материя не может исчезнуть или возникнуть спонтанно. ^[2]^: 59–62

Поэтому балансы масс широко используются в инженерном и экологическом анализе . Например, теория баланса массы используется для проектирования химических реакторов , для анализа альтернативных процессов производства химических веществ, а также для моделирования рассеивания загрязнений и других процессов в физических системах. Массовые балансы составляют основу проектирования технологических процессов. ^[3] Тесно связанные и дополняющие друг друга методы анализа включают баланс населения , энергетический баланс и несколько более сложный энтропии баланс . Эти методы необходимы для тщательного проектирования и анализа таких систем, как холодильный цикл .

В экологическом мониторинге термин « бюджетные расчеты» используется для описания уравнений массового баланса, где они используются для оценки данных мониторинга (сравнение входных и выходных данных и т. д.). В биологии теория динамического баланса энергии для метаболической организации явно использует баланс массы и энергии.

Введение

Общая форма баланса масс такова: Масса, поступающая в систему, должна в силу сохранения массы либо покинуть систему, либо накопиться внутри системы .

Математически баланс масс для системы без химической реакции выглядит следующим образом: ^[2]^: 59–62

${\text{Input}}={\text{Output}}+{\text{Accumulation}}$

Строго говоря, приведенное выше уравнение справедливо и для систем с химическими реакциями , если члены в уравнении баланса понимать общую массу, то есть сумму всех химических веществ системы. В отсутствие химической реакции количество любых химических веществ, входящих и выходящих, будет одинаковым; это приводит к уравнению для каждого вида, присутствующего в системе. Однако если это не так, то в уравнение баланса массы необходимо внести поправки, чтобы учесть образование или истощение (потребление) каждого химического вещества. Некоторые используют один член в этом уравнении для учета химических реакций, которые будут отрицательными при истощении и положительными при выработке. Однако общепринятая форма этого уравнения написана для учета как положительного члена образования (т.е. продукта реакции), так и отрицательного члена потребления (реагентов, используемых для производства продуктов). Хотя в целом общий баланс в системе будет определяться одним слагаемым, если это уравнение баланса должно быть применено к отдельному виду, а затем ко всему процессу, необходимы оба слагаемых. Это модифицированное уравнение можно использовать не только для реактивных систем, но и для балансов населения, возникающих в механики частиц задачи . Уравнение приведено ниже; Обратите внимание, что оно упрощается до предыдущего уравнения в случае, когда член генерации равен нулю. ^[2]^: 59–62

${\text{Input}}+{\text{Generation}}={\text{Output}}+{\text{Accumulation}}\ +{\text{Consumption}}$

В отсутствие ядерной реакции число атомов , входящих и выходящих, должно оставаться неизменным даже при наличии химической реакции.
Для формирования баланса необходимо четко определить границы системы.
Балансы масс могут быть рассчитаны для физических систем в разных масштабах.
Балансы массы можно упростить, предположив устойчивое состояние , в котором срок накопления равен нулю.

Показательный пример

Простой пример может проиллюстрировать эту концепцию. Рассмотрим ситуацию, когда суспензия течет в отстойник для удаления твердых частиц из резервуара. Твердые частицы собираются внизу с помощью конвейерной ленты, частично погруженной в резервуар, а вода выходит через переливное отверстие.

В этом примере есть два вещества: твердые вещества и вода. Выход для перелива воды несет повышенную концентрацию воды по отношению к твердым частицам по сравнению с входом для шлама, а выход конвейерной ленты несет повышенную концентрацию твердых частиц по сравнению с водой.

Предположения

Устойчивое состояние
Нереактивная система

Анализ

Предположим, что входной состав пульпы (по массе) состоит из 50% твердых веществ и 50% воды, при массовом расходе 100 кг / мин . Предполагается, что резервуар работает в устойчивом состоянии, и поскольку такое накопление равно нулю, поэтому вход и выход должны быть равны как для твердых частиц, так и для воды. Если мы знаем, что эффективность удаления шламового бака составляет 60%, то на выходе воды будет 20 кг / мин твердых частиц (40% умножить на 100 кг / мин умножить на 50% твердых частиц). Если мы измерим скорость потока объединенных твердых веществ и воды и получим, что выход воды равен 65 кг / мин , то количество воды, выходящей через конвейерную ленту, должно составлять 5 кг / мин . Это позволяет нам полностью определить, как масса была распределена в системе, имея лишь ограниченную информацию и используя соотношения баланса массы на границах системы. Массовый баланс для этой системы можно описать в табличной форме:

Массовый баланс для осветлителя
	Транслировать
Материал	Вход осветлителя	Выход осветленной воды	Извлеченные твердые вещества
Твердые вещества	50 кг/мин	20 кг/мин	30 кг/мин
Вода	50 кг/мин	45 кг/мин	5 кг/мин
Общий	100 кг/мин	65 кг/мин	35 кг/мин

Массовая обратная связь (переработка)

Градирни являются хорошим примером системы рециркуляции.

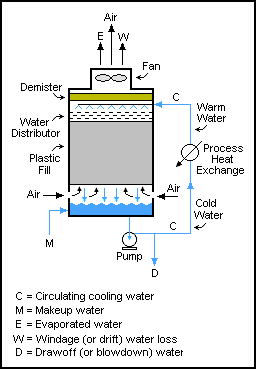
Массовые балансы могут выполняться в системах с циклическими потоками. В этих системах выходные потоки возвращаются на вход устройства, часто для дальнейшей переработки. ^[2]^: 97–105

Такие системы распространены в цепях измельчения , где зерно измельчается, а затем просеивается, чтобы из контура выходили только мелкие частицы, а более крупные частицы возвращаются в вальцовую мельницу (измельчитель). Однако потоки рециркуляции ни в коем случае не ограничиваются операциями в области механики твердого тела; они также используются в потоках жидкости и газа. Одним из таких примеров являются градирни , где вода прокачивается через башню много раз, при этом при каждом проходе отбирается лишь небольшое количество воды (чтобы предотвратить накопление твердых частиц), пока она не испарится или не выйдет вместе с отведенной водой. Массовый баланс воды равен $M = D + W +$ E.

Использование рециркуляции помогает повысить общую конверсию входных продуктов, что полезно для процессов конверсии с малым количеством проходов (таких как процесс Хабера ).

Дифференциальные массовые балансы

Массовый баланс также можно принять дифференцированно . Концепция та же, что и для большого баланса масс, но она выполняется в рамках предельной системы (например, можно рассмотреть предельный случай по времени или, чаще, по объему). Дифференциальный баланс масс используется для создания дифференциальных уравнений , которые могут стать эффективным инструментом для моделирования и понимания целевой системы.

Дифференциальный баланс масс обычно решается в два этапа: сначала необходимо получить набор основных дифференциальных уравнений, а затем эти уравнения необходимо решить либо аналитически, либо, для менее решаемых задач, численно.

Следующие системы являются хорошими примерами применения дифференциального баланса масс:

Идеальный реактор периодического действия (с перемешиванием)
Идеальный резервуарный реактор, также называемый резервуарным реактором непрерывного действия (CSTR).
Идеальный реактор поршневого типа (PFR)

Идеальный реактор периодического действия

Идеальный реактор периодического действия полностью смешанного типа представляет собой закрытую систему. изотермические условия , и смешивание предотвращает градиенты концентрации, поскольку концентрации реагентов уменьшаются, а концентрации продуктов увеличиваются с течением времени. Предполагаются ^[4]^: 40–41 Многие учебники по химии, когда пишут о кинетике реакций и химическом равновесии , неявно предполагают, что изучаемую систему можно описать как реактор периодического действия .Массовый баланс вещества А будет равен

${\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\0&+&r_{\rm {A}}V&=&0&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}$

где

$r A$ обозначает скорость, с которой производится вещество А;
$V$ – объем (который может быть постоянным или нет);
$n A$ количество молей ( $n$ ) вещества А.

В реакторе периодического действия с подпиткой некоторые реагенты/ингредиенты добавляются непрерывно или импульсами (сравните приготовление каши, либо сначала смешивая все ингредиенты, а затем давая ей закипеть, что можно описать как реактор периодического действия, либо сначала смешивая только воду и соль и доведение до кипения перед добавлением других ингредиентов, что можно назвать реактором периодического действия с подпиткой). Массовые балансы для реакторов с подпиткой становятся немного сложнее.

Реактивный пример

В первом примере мы покажем, как использовать массовый баланс для получения зависимости между процентом избытка воздуха для сгорания мазута на углеводородной основе и процентом кислорода в газе, являющемся продуктом сгорания. Во-первых, обычный сухой воздух содержит 0,2095 моль кислорода на моль воздуха, то есть один моль O.
₂ на 4,773 моль сухого воздуха. Для стехиометрического сгорания соотношение между массой воздуха и массой каждого горючего элемента в мазуте равно:

${\begin{array}{rccc}{\text{Carbon:}}&{\frac {\text{mass of air}}{\text{mass of C}}}&=&{\frac {4.773\times 28.96}{12.01}}&=&11.51\\[2pt]{\text{Hydrogen:}}&{\frac {\text{mass of air}}{\text{mass of H}}}&=&{\frac {{\frac {1}{4}}(4.773)\times 28.96}{1.008}}&=&34.28\\[6pt]{\text{Sulfur:}}&{\frac {\text{mass of air}}{\text{mass of S}}}&=&{\frac {4.773\times 28.96}{32.06}}&=&4.31\end{array}}$

Учитывая точность типичных аналитических процедур, уравнение массы воздуха на массу топлива при стехиометрическом сгорании имеет вид:

${\frac {\text{mass of air}}{\text{mass of fuel}}}=\mathrm {AFR} _{\text{mass}}=11.5\,w_{\rm {C}}+34.3\,w_{\rm {H}}+(w_{\rm {S}}-w_{\rm {O}})$

где $w C, w H, w S, w O$ относятся к массовой доле каждого элемента в мазуте, сера сгорает до SO ₂ и $AFR масса$ относятся к воздушно-топливному соотношению в единицах массы.

Для 1 кг мазута, содержащего 86,1% C, 13,6% H, 0,2% O и 0,1% S, стехиометрическая масса воздуха равна 14,56 кг , поэтому AFR = 14,56. Тогда масса продукта сгорания составит 15,56 кг . При точной стехиометрии O
₂ должно отсутствовать. При 15-процентном избытке воздуха АФР = 16,75, а масса газа-продукта сгорания равна 17,75 кг , в котором содержится 0,505 кг избыточного кислорода. Таким образом, дымовой газ содержит 2,84 процента O.
₂ по массе. Соотношения между процентом избытка воздуха и % O
₂ в дымовых газах точно выражаются квадратными уравнениями, действительными в диапазоне 0–30 процентов избытка воздуха:

${\begin{aligned}&\%{\text{ excess air}}=1.2804\times (\%{\ce {O2}}{\text{ in combustion gas}})^{2}+4.49\times (\%{\ce {O2}}{\text{ in combustion gas}})\\[4pt]&\%{\ce {O2}}{\text{ in combustion gas}}=-0.00138\times (\%{\text{ excess air}})^{2}+0.210\times (\%{\text{ excess air}})\end{aligned}}$

Во втором примере мы воспользуемся законом действия масс , чтобы вывести выражение для константы химического равновесия .

Предположим, у нас есть закрытый реактор, в котором протекает следующая обратимая реакция в жидкой фазе:

$a\mathrm {A} +b\mathrm {B} \leftrightarrow c\mathrm {C} +d\mathrm {D}$

Массовый баланс вещества А становится

${\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\0&+&r_{\rm {A}}V&=&0&+&\displaystyle {\frac {dn_{\mathrm {A} }}{dt}}\end{array}}$

Поскольку у нас есть жидкофазная реакция, мы можем (обычно) предположить постоянный объем, и поскольку $n_{\rm {A}}=V*C_{\rm {A}}$ мы получаем

$r_{\rm {A}}V=V{\frac {dC_{\rm {A}}}{dt}}$

или

$r_{\rm {A}}={\frac {dC_{\rm {A}}}{dt}}$

Во многих учебниках это дается как определение скорости реакции без указания неявного предположения, что речь идет о скорости реакции в закрытой системе только с одной реакцией. Это досадная ошибка, которая на протяжении многих лет сбивала с толку многих студентов.

По закону действия масс скорость прямой реакции можно записать как

$r_{1}=k_{1}[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}$

а скорость обратной реакции как

$r_{-1}=k_{-1}[\mathrm {C} ]^{c}[\mathrm {D} ]^{d}$

Таким образом, скорость производства вещества А равна

$r_{\mathrm {A} }=a(r_{-1}-r_{1})$

и поскольку в состоянии равновесия концентрация A постоянна, мы получаем

$r_{\mathrm {A} }=a(r_{-1}-r_{1})={\frac {dC_{\mathrm {A} }}{dt}}=0$

или переставить

${\frac {k_{1}}{k_{-1}}}={\frac {[\mathrm {C} ]^{c}[\mathrm {D} ]^{d}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}=K_{eq}$

Идеальный резервуарный реактор/резервуарный реактор непрерывного перемешивания

Реактор непрерывного смешения представляет собой открытую систему с входящим потоком реагентов и выходящим потоком продуктов. ^[4]^: 41 Озеро можно рассматривать как реактор-резервуар, а озера с длительным временем оборота (например, с низким отношением потока к объему) для многих целей можно рассматривать как постоянно перемешиваемые (например, гомогенные во всех отношениях). Тогда баланс масс станет

${\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\Q_{0}\cdot C_{\rm {A,0}}&+&r_{\rm {A}}\cdot V&=&Q\cdot C_{\rm {A}}&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}$

где

$Q 0$ – объемный расход в системе;
$Q$ – объемный расход из системы;
$C A,0$ – концентрация A в притоке ;
$CA —$ концентрация A в оттоке .

В открытой системе мы никогда не сможем достичь химического равновесия. Однако мы можем достичь устойчивого состояния , в котором все переменные состояния (температура, концентрации и т. д.) остаются постоянными ( $ACC = 0$ ).

Пример

Представьте себе ванну, в которой растворено немного соли для купания. Теперь заливаем больше воды, оставляя нижнюю пробку закрытой. Что происходит?

Поскольку реакции нет, $PROD = 0$ и поскольку оттока нет $Q = 0$ . Массовый баланс становится

${\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\Q_{0}\cdot C_{\rm {A,0}}&+&0&=&0\cdot C_{\rm {A}}&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}$

или

$Q_{0}\cdot C_{\rm {A,0}}={\frac {dC_{\rm {A}}V}{dt}}=V{\frac {dC_{\rm {A}}}{dt}}+C_{\rm {A}}{\frac {dV}{dt}}$

Однако, используя баланс массы для общего объема, очевидно, что ${\tfrac {dV}{dt}}=Q_{0}$ и это $V=V_{t=0}+Q_{0}t.$ Таким образом мы получаем

${\frac {dC_{\rm {A}}}{dt}}={\frac {Q_{0}}{(V_{t=0}+Q_{0}t)}}\left(C_{\rm {A,0}}-C_{\rm {A}}\right)$

Обратите внимание, что здесь нет реакции и, следовательно, нет скорости реакции или закона скорости , и тем не менее ${\tfrac {dC_{\rm {A}}}{dt}}\neq 0$ . Таким образом, мы можем сделать вывод, что скорость реакции не может быть определена в общем виде с помощью ${\tfrac {dC}{dt}}$ . чем установить Прежде связь между ${\tfrac {dC}{dt}}$ и можно найти скорость реакции. Однако во многих учебниках скорость реакции определяется как

$r={\frac {dC_{\mathrm {A} }}{dt}}$

не говоря уже о том, что это определение неявно предполагает, что система замкнута, имеет постоянный объем и существует только одна реакция.

Идеальный реактор поршневого типа (PFR)

Идеализированный реактор поршневого потока представляет собой открытую систему, напоминающую трубу, без перемешивания в направлении потока, но с идеальным перемешиванием, перпендикулярным направлению потока, часто используемую для таких систем, как реки и водопроводы, если поток турбулентный. Когда составляется баланс массы для трубки, сначала рассматривают бесконечно малую часть трубки и составляют баланс массы по ней, используя идеальную модель реактора-резервуара. ^[4]^: 46–47 Затем этот массовый баланс интегрируется по всему объему реактора, чтобы получить:

${\frac {d(Q\cdot C_{\rm {A}})}{dV}}=r_{\rm {A}}$

В числовых решениях, например, при использовании компьютеров, идеальная труба часто преобразуется в серию резервуарных реакторов, поскольку можно показать, что PFR эквивалентен бесконечному количеству последовательно соединенных резервуаров с перемешиванием, но последнее часто легче анализировать. , особенно в устойчивом состоянии.

Более сложные проблемы

В действительности реакторы часто неидеальны, и для описания системы используются комбинации приведенных выше моделей реакторов. Не только скорости химических реакций, но и скорости массопереноса могут иметь значение при математическом описании системы, особенно в гетерогенных системах. ^[5]

Поскольку скорость химической реакции зависит от температуры, часто необходимо составить как энергетический баланс (часто тепловой баланс, а не полноценный энергетический баланс), так и массовые балансы для полного описания системы. Для энергетического баланса может потребоваться другая модель реактора: система, закрытая по массе, может быть открытой по энергии, например, поскольку тепло может поступать в систему посредством проводимости .

Коммерческое использование

На промышленных технологических предприятиях, учитывая тот факт, что масса, входящая и выходящая из любой части технологического предприятия, должна быть сбалансирована, алгоритмы проверки и согласования данных могут использоваться для корректировки измеренных расходов при условии, что существует достаточная избыточность измерений расхода, чтобы обеспечить статистическое согласование и исключение. обнаруживаемых ошибочных измерений. Поскольку все измеренные значения в реальном мире содержат неотъемлемую ошибку, сверенные измерения обеспечивают лучшую основу, чем измеренные значения, для финансовой отчетности, оптимизации и нормативной отчетности. Существуют пакеты программного обеспечения, позволяющие сделать это коммерчески осуществимым на ежедневной основе.

См. также

Ссылки

^ Нандагопал, Н.С. (2023). Принципы и приложения химической инженерии . Спрингер.
^ Перейти обратно: ^а ^б ^с ^д Химмельблау, Дэвид М. (1967). Основные принципы и расчеты в химической технологии (2-е изд.). Прентис Холл .
^ Синнотт, РК (2005). Химическая инженерия Коулсона и Ричардсона (4-е изд.). Амстердам Париж: Эльзевир Баттерворт-Хайнеманн. п. 34. ISBN 978-0-7506-6538-4 .
^ Перейти обратно: ^а ^б ^с Вебер, Уолтер младший (1972). Физико-химические процессы контроля качества воды . Уайли-Интерсайенс . ISBN 0-471-92435-0 .
^ Перри, Роберт Х.; Чилтон, Сесил Х.; Киркпатрик, Сидни Д. (1963). Справочник инженеров-химиков (четвертое изд.). МакГроу-Хилл . стр. 4–21.

Внешние ссылки

[1] Нандагопал, Н.С. (2023). Принципы и приложения химической инженерии . Спрингер.

[himmelblau-2] Перейти обратно: ^а ^б ^с ^д Химмельблау, Дэвид М. (1967). Основные принципы и расчеты в химической технологии (2-е изд.). Прентис Холл .

[3] Синнотт, РК (2005). Химическая инженерия Коулсона и Ричардсона (4-е изд.). Амстердам Париж: Эльзевир Баттерворт-Хайнеманн. п. 34. ISBN 978-0-7506-6538-4 .

[weber-4] Перейти обратно: ^а ^б ^с Вебер, Уолтер младший (1972). Физико-химические процессы контроля качества воды . Уайли-Интерсайенс . ISBN 0-471-92435-0 .

[Perry_1963_4–21-5] Перри, Роберт Х.; Чилтон, Сесил Х.; Киркпатрик, Сидни Д. (1963). Справочник инженеров-химиков (четвертое изд.). МакГроу-Хилл . стр. 4–21.

[1]

[2]

[3]

[4]

[5]