Стандартное дополнение

Стандартный метод добавления , часто используемый в аналитической химии , позволяет количественно определить присутствие аналита в неизвестном виде. Этот метод полезен для анализа сложных образцов, в которых эффект матрицы мешает сигналу аналита. По сравнению с методом калибровочной кривой метод сложения стандартов имеет преимущество, заключающееся в том, что матрицы неизвестных и стандартов практически идентичны. Это сводит к минимуму потенциальную погрешность, возникающую из-за эффекта матрицы при определении концентрации.

Вариации

Стандартное добавление предполагает добавление известного количества аналита к неизвестному образцу. Этот процесс известен как добавление . Увеличивая количество пиков, аналитик может экстраполировать концентрацию аналита в неизвестном направлении, в котором не было пиков. Существует несколько подходов к стандартному дополнению. В следующем разделе кратко излагаются каждый подход.

Единственная стандартная добавка, используемая в полярографии.

В классической полярографии стандартный метод добавления предполагает создание двух образцов — одного образца без выбросов, а другого — с выбросами. Сравнивая ток, измеренный в двух образцах, определяют количество неизвестного аналита. Этот подход был первым зарегистрированным использованием стандартных добавок и был предложен немецким горным химиком Хансом Хоном в 1937 году. В своей практической книге по полярографии под названием Chemische Analysen mit dem Polargraphen Хон назвал этот метод Eizhusatzes , что на английском языке переводится как «калибровочное сложение». Позже в немецкой литературе этот метод получил название Standardzugabe , что в переводе с английского означает «стандартное сложение».

Современная полярография обычно предполагает использование трех растворов: стандартного раствора, неизвестного раствора и смеси стандартного и неизвестного раствора. Измеряя любые два из этих растворов, вычисляют неизвестную концентрацию.

Поскольку добавление полярографического стандарта предполагает использование только одного раствора с добавленным стандартом – двухуровневой конструкции, полярографы всегда называют этот метод единичным, стандартным добавлением.

Последовательное добавление стандартов в постоянной пробе и общем объеме.

Помимо области полярографии, книга Харви «Спектрохимические процедуры» была следующим ранним справочником, в котором упоминалось присоединение стандартов. Подход Харви, который предполагает последовательное добавление стандартов, очень напоминает наиболее часто используемый сегодня метод добавления стандартов.

Чтобы применить этот метод, аналитики готовят несколько растворов, содержащих равные количества неизвестного вещества, и добавляют в них различные концентрации аналита. Количество неизвестного вещества и общий объем одинаковы для всех стандартов, и единственная разница между стандартами заключается в количестве добавленного аналита. Это приводит к линейной зависимости между сигналом аналита и количеством добавленного аналита, что позволяет определить концентрацию неизвестного аналита путем экстраполяции нулевого сигнала аналита. Одним из недостатков этого подхода является то, что он требует достаточного количества неизвестного. При работе с ограниченным объемом выборки аналитику может потребоваться сделать одно добавление, но обычно считается лучшей практикой делать по крайней мере два добавления, когда это возможно.

Обратите внимание, что это не ограничивается жидкими образцами. в атомно-абсорбционной спектроскопии часто используются стандартные добавки с твердым веществом в качестве образца. Например,

В атомно-эмиссионной спектроскопии фоновый сигнал не может быть разрешен стандартным сложением. Таким образом, фоновый сигнал необходимо вычесть из неизвестной и стандартной интенсивности перед экстраполяцией нулевого сигнала.

Поскольку этот подход предполагает добавление различного количества стандартов, во множественном числе его часто называют « дополнениями к стандартам» .

Пример

Предположим, аналитик определяет концентрацию серебра в образцах отработанного раствора фотопленки методом атомно-абсорбционной спектроскопии . Используя метод калибровочной кривой, аналитик может откалибровать спектрометр чистого серебра с использованием водных растворов и использовать калибровочный график для определения количества серебра, присутствующего в образцах отходов. Однако этот метод предполагает, что чистый водный раствор серебра и образец фотографических отходов имеют одинаковую матрицу и, следовательно, образцы отходов не имеют матричного эффекта.

Таблица с примером стандартной добавки для определения концентрации серебра в отходах фотопленки. Пожалуйста, обратитесь к разделу «Ограничения и неопределенность стандартного дополнения» для получения дополнительной информации о том, как рассчитать часть анализа ошибок. Концентрация серебра в тестируемом образце представляет собой точку пересечения оси x графика. Коэффициент разбавления умножается на эту начальную концентрацию, чтобы определить исходную концентрацию.

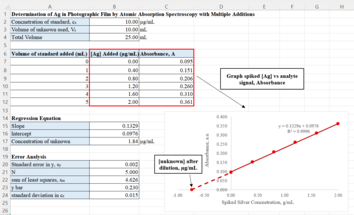
Матричные эффекты возникают даже при использовании таких методов, как плазменная спектрометрия , которые имеют репутацию относительно свободных от помех. Таким образом, в этом случае аналитик будет использовать стандартные дополнения.

Для стандартных добавок берутся равные объемы растворов пробы, и в каждый из них отдельно добавляются различные количества аналита – 0, 1, 2, 3, 4, 5 мл, где добавление 0 мл представляет собой чистый раствор тестируемой пробы. Затем все растворы разбавляют до одинакового объема 25 мл, используя тот же растворитель, который использовался для приготовления растворов для добавления. Каждый приготовленный раствор затем анализируется с помощью атомно-абсорбционного спектрометра. Результирующие сигналы и соответствующие концентрации добавленного серебра нанесены на график, где концентрация отложена по оси x, а сигнал - по оси y. Линия регрессии рассчитывается посредством анализа наименьших квадратов , а точка пересечения оси X определяется соотношением точки пересечения оси Y и наклона линии регрессии. Этот пересечение оси x представляет собой концентрацию серебра в испытуемом образце, в который не добавлен стандартный раствор. 

Ошибка

Хотя метод стандартного сложения эффективен для снижения влияния большинства эффектов матрицы на сигнал аналита, он не может корректировать эффекты поступательной матрицы. Эти эффекты вызваны другими веществами, присутствующими в неизвестном образце, которые часто не зависят от концентрации аналита. Их обычно называют «фоновыми», и они могут влиять на точку пересечения линии регрессии, не влияя на наклон. Это приводит к смещению в сторону неизвестной концентрации. Другими словами, стандартное сложение не будет корректировать этот фон или другие спектральные помехи.

Аналитикам также необходимо оценить точность определения неизвестной концентрации путем расчета стандартного отклонения. $s_{x}$. Ниже $s_{x}$ указывает на большую точность измерений. Стоимость $s_{x}$ дается

$s_{x}={\frac {s_{y}}{|m|}}{\sqrt {{\frac {1}{n}}+{\frac {{\bar {y}}^{2}}{m^{2}\sum {(x_{i}-{\bar {x}})^{2}}}}}}$

где в расчете участвуют следующие переменные:

• стандартное отклонение остатков, $s_{y}$ $={\sqrt {\frac {\sum {(y_{i}-mx_{i}-b)}^{2}}{n-2}}}$
• абсолютное значение наклона линии наименьших квадратов, $m$
• y-пересечение линейной кривой, $b$
• количество стандартов, $n$
• среднее измерение эталонов, ${\bar {y}}$
• концентрации стандартов, $x_{i}$
• средняя концентрация стандартов, ${\bar {x}}$

См. также

• Стандартная кривая
• Изотопное разбавление
• Внутренний стандарт