Сеть радиальных базисных функций
В области математического моделирования сеть радиальных базисных функций представляет собой искусственную нейронную сеть , которая использует радиальные базисные функции в качестве функций активации . Выход сети представляет собой линейную комбинацию радиальных базисных функций входов и параметров нейрона. Сети радиальных базисных функций имеют множество применений, включая аппроксимацию функций , прогнозирование временных рядов , классификацию и управление системой . Впервые они были сформулированы в статье 1988 года Брумхедом и Лоу, исследователями из Королевского института сигналов и радаров . [1] [2] [3]
Сетевая архитектура
[ редактировать ]
Сети с радиальной базисной функцией (RBF) обычно имеют три уровня: входной уровень, скрытый уровень с нелинейной функцией активации RBF и линейный выходной уровень. Входные данные можно смоделировать как вектор действительных чисел. . Выходной сигнал сети тогда является скалярной функцией входного вектора: , и определяется выражением
где — количество нейронов в скрытом слое, центральный вектор нейрона , и это вес нейрона в линейном выходном нейроне. Функции, которые зависят только от расстояния от центрального вектора, радиально симметричны относительно этого вектора, отсюда и название радиальная базисная функция. В базовой форме все входы подключены к каждому скрытому нейрону. обычно За норму принимается евклидово расстояние (хотя расстояние Махаланобиса , по-видимому, лучше работает с распознаванием образов). [4] [5] [ редакция ] ), а радиальная базисная функция обычно считается гауссовой
- .
Гауссовы базисные функции локальны по отношению к центральному вектору в том смысле, что
т.е. изменение параметров одного нейрона имеет лишь небольшой эффект для входных значений, которые находятся далеко от центра этого нейрона.
При определенных мягких условиях на форму функции активации сети RBF являются аппроксиматорами подмножества компактного универсальными . [6] Это означает, что RBF-сеть с достаточным количеством скрытых нейронов может аппроксимировать любую непрерывную функцию на замкнутом ограниченном множестве с произвольной точностью.
Параметры , , и определяются таким образом, который оптимизирует соответствие между и данные.

Нормализованный
[ редактировать ]Нормализованная архитектура
[ редактировать ]Помимо вышеописанной ненормализованной архитектуры, сети RBF могут быть нормализованы . В этом случае отображение
где
известна как нормализованная радиальная базисная функция .
Теоретическая мотивация нормализации
[ редактировать ]Существует теоретическое обоснование такой архитектуры в случае стохастического потока данных. Предположим , что используется стохастическое ядро для совместной плотности вероятности.
где веса и являются образцами данных, и мы требуем, чтобы ядра были нормализованы
и
- .
Плотности вероятности во входном и выходном пространствах равны
и
Ожидание y с учетом входных данных является
где
- условная вероятность y при условии .Условная вероятность связана с совместной вероятностью посредством теоремы Байеса.
что дает
- .
Это становится
когда выполняются интеграции.
Локальные линейные модели
[ редактировать ]Иногда удобно расширить архитектуру, включив в нее локальные линейные модели. В этом случае архитектуры становятся, в первую очередь,
и
в ненормированном и нормализованном случаях соответственно. Здесь являются весами, подлежащими определению. Возможны также линейные члены более высокого порядка.
Этот результат можно записать
где
и
в ненормированном случае и
в нормированном случае.
Здесь представляет собой дельта-функцию Кронекера, определяемую как
- .
Обучение
[ редактировать ]Сети RBF обычно обучаются на основе пар входных и целевых значений. , по двухшаговому алгоритму.
На первом этапе центральные векторы функций RBF в скрытом слое. Этот шаг можно выполнить несколькими способами; центры могут быть выбраны случайным образом из некоторого набора примеров или они могут быть определены с помощью кластеризации k-средних . Обратите внимание, что этот шаг не контролируется .
Второй шаг просто соответствует линейной модели с коэффициентами к выводам скрытого слоя относительно некоторой целевой функции. Общей целевой функцией, по крайней мере для оценки регрессии/функции, является функция наименьших квадратов:
где
- .
Мы явно включили зависимость от весов. Минимизация целевой функции наименьших квадратов за счет оптимального выбора весов оптимизирует точность подбора.
Бывают случаи, когда необходимо оптимизировать несколько целей, таких как плавность и точность. В этом случае полезно оптимизировать регуляризованную целевую функцию, такую как
где
и
где оптимизация S максимизирует гладкость и известен как параметр регуляризации .
Третий дополнительный шаг обратного распространения ошибки может быть выполнен для точной настройки всех параметров сети RBF. [3]
Интерполяция
[ редактировать ]Сети RBF можно использовать для интерполяции функции. когда значения этой функции известны в конечном числе точек: . Взяв известные точки быть центрами радиальных базисных функций и оценивать значения базисных функций в тех же точках веса можно решить из уравнения
Можно показать, что интерполяционная матрица в приведенном выше уравнении невырождена, если точки различны, поэтому веса можно решить простой линейной алгеброй:
где .
Аппроксимация функции
[ редактировать ]Если целью является не выполнение строгой интерполяции, а более общая аппроксимация или классификация функций, оптимизация несколько сложнее, поскольку нет очевидного выбора для центров. Обучение обычно проводится в два этапа: сначала фиксируется ширина и центры, а затем вес. Это можно оправдать, если принять во внимание различную природу нелинейных скрытых нейронов и линейного выходного нейрона.
Обучение базовых функциональных центров
[ редактировать ]Центры базисных функций могут быть случайным образом выбраны среди входных экземпляров или получены с помощью алгоритма ортогонального наименьших квадратов или найдены путем кластеризации выборок и выбора средних значений кластера в качестве центров.
Ширина RBF обычно фиксируется на одном и том же значении, пропорциональном максимальному расстоянию между выбранными центрами.
Псевдообратное решение для линейных весов
[ редактировать ]После центров были фиксированы, веса, которые минимизируют ошибку на выходе, можно вычислить с помощью линейного псевдообратного решения:
- ,
где элементы G представляют собой значения радиальных базисных функций, оцененных в точках : .
Существование этого линейного решения означает, что в отличие от сетей многослойного перцептрона (MLP), сети RBF имеют явный минимизатор (когда центры фиксированы).
Обучение градиентному спуску линейных весов
[ редактировать ]Другой возможный алгоритм обучения — градиентный спуск . При обучении градиентному спуску веса корректируются на каждом временном шаге путем перемещения их в направлении, противоположном градиенту целевой функции (таким образом позволяя найти минимум целевой функции),
где является «параметром обучения».
В случае обучения линейных весов , алгоритм становится
в ненормированном случае и
в нормированном случае.
Для локальных линейных архитектур обучение градиентному спуску
Обучение операторов проектирования линейных весов
[ редактировать ]В случае обучения линейных весов и , алгоритм становится
в ненормированном случае и
в нормированном случае и
в локально-линейном случае.
Для одной базовой функции обучение операторов прогнозирования сводится к методу Ньютона .

Примеры
[ редактировать ]Логистическая карта
[ редактировать ]Основные свойства радиальных базисных функций можно проиллюстрировать с помощью простой математической карты, логистической карты , которая отображает единичный интервал сам на себя. Его можно использовать для создания удобного потока данных прототипа. Логистическую карту можно использовать для изучения аппроксимации функций , прогнозирования временных рядов и теории управления . Карта возникла из области динамики населения и стала прототипом хаотических временных рядов. Карта в полностью хаотическом режиме имеет вид
где t — индекс времени. Значение x в момент времени t+1 является параболической функцией x в момент времени t. Это уравнение представляет собой основную геометрию хаотического временного ряда, созданного логистической картой.
Генерация временного ряда из этого уравнения является прямой задачей . Приведенные здесь примеры иллюстрируют обратную задачу ; идентификация основной динамики или фундаментального уравнения логистической карты на основе образцов временного ряда. Цель – найти оценку
для ф.
Аппроксимация функции
[ редактировать ]Ненормированные радиальные базисные функции
[ редактировать ]Архитектура
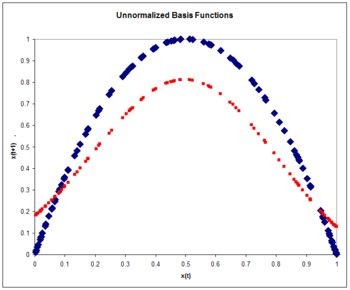
где
- .
Поскольку входные данные являются скаляром , а не вектором , размерность входных данных равна единице. Мы выбираем количество базисных функций N = 5 и размер обучающего набора, равный 100 экземплярам, сгенерированным хаотичным временным рядом. Вес принимается константа, равная 5. Веса пять примеров из временного ряда. Веса проходят подготовку операторов проекции:
где скорость обучения принимается равным 0,3. Обучение осуществляется за один проход по 100 тренировочным точкам. Среднеквадратическая ошибка составляет 0,15.
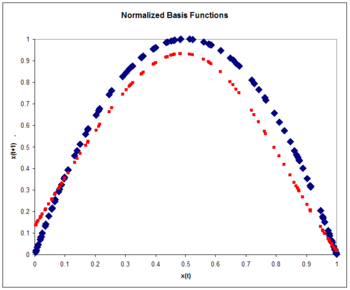
Нормализованные радиальные базисные функции
[ редактировать ]Нормализованная архитектура RBF
где
- .
Снова:
- .
Опять же, мы выбираем количество базисных функций равным пяти, а размер обучающего набора — 100 экземпляров, сгенерированных хаотичным временным рядом. Вес принимается константа, равная 6. Веса пять примеров из временного ряда. Веса проходят подготовку операторов проекции:
где скорость обучения снова принимается равным 0,3. Обучение проводится за один проход по 100 тренировочным точкам. Среднеквадратическая ошибка на тестовом наборе из 100 образцов составляет 0,084, что меньше ненормализованной ошибки. Нормализация приводит к повышению точности. Обычно точность нормализованных базисных функций увеличивается даже больше, чем ненормализованных функций, по мере увеличения размерности входных данных.

Прогнозирование временных рядов
[ редактировать ]После оценки базовой геометрии временного ряда, как в предыдущих примерах, прогноз временного ряда можно сделать путем итерации:
- .
На рисунке показано сравнение фактического и расчетного временных рядов. Предполагаемый временной ряд начинается в нулевой момент времени с точным знанием x(0). Затем он использует оценку динамики для обновления оценки временного ряда для нескольких временных шагов.
Обратите внимание, что оценка точна только для нескольких временных шагов. Это общая характеристика хаотических временных рядов. Это свойство чувствительной зависимости от начальных условий, характерное для хаотических временных рядов. Небольшая первоначальная ошибка со временем усиливается. Мера расхождения временных рядов с почти одинаковыми начальными условиями известна как показатель Ляпунова .
Управление хаотичным временным рядом
[ редактировать ]
Мы предполагаем, что выходными данными логистической карты можно манипулировать с помощью управляющего параметра. такой, что
- .
Цель состоит в том, чтобы выбрать параметр управления таким образом, чтобы привести временной ряд к желаемому результату. . Это можно сделать, если мы выберем параметр управления в качестве
где
является приближением к основной естественной динамике системы.
Алгоритм обучения имеет вид
где
- .
См. также
[ редактировать ]- Ядро радиальной базисной функции
- обучение на основе примеров
- Адаптивное табулирование in situ
- Прогнозная аналитика
- Теория хаоса
- Иерархический RBF
- Контроллер артикуляции модели мозжечка
- Мгновенно обучаемые нейронные сети
Ссылки
[ редактировать ]- ^ Брумхед, Д.С.; Лоу, Дэвид (1988). Радиальные базисные функции, многопараметрическая функциональная интерполяция и адаптивные сети (Технический отчет). РСРЭ . 4148. Архивировано из оригинала 9 апреля 2013 года.
- ^ Брумхед, Д.С.; Лоу, Дэвид (1988). «Многомерная функциональная интерполяция и адаптивные сети» (PDF) . Сложные системы . 2 : 321–355. Архивировано (PDF) из оригинала 1 декабря 2020 г. Проверено 29 января 2019 г.
- ^ Jump up to: а б Швенкер, Фридхельм; Кестлер, Ганс А.; Пальм, Гюнтер (2001). «Три этапа обучения для сетей с радиальными базисными функциями». Нейронные сети . 14 (4–5): 439–458. CiteSeerX 10.1.1.109.312 . дои : 10.1016/s0893-6080(01)00027-2 . ПМИД 11411631 .
- ^ Бехайм, Ларби; Зитуни, Адель; Беллуар, Фабьен (январь 2004 г.). «Новый классификатор нейронных сетей RBF с оптимизированным количеством скрытых нейронов» .
- ^ Ибрикчи, Тургай; Брандт, Мэн; Ван, Гуаньюй; Ачиккар, Мустафа (23–26 октября 2002 г.). Расстояние Махаланобиса с радиальной сетью базисных функций на вторичных структурах белка . Материалы второй совместной 24-й ежегодной конференции и ежегодного осеннего собрания Общества биомедицинской инженерии . Общество инженерии в медицине и биологии, материалы ежегодной международной конференции IEEE . Том. 3. Хьюстон, Техас, США (опубликовано 6 января 2003 г.). стр. 2184–5. дои : 10.1109/IEMBS.2002.1053230 . ISBN 0-7803-7612-9 . ISSN 1094-687X .
- ^ Парк, Дж.; И.В. Сандберг (лето 1991 г.). «Универсальное приближение с использованием сетей с радиальными базисными функциями». Нейронные вычисления . 3 (2): 246–257. дои : 10.1162/neco.1991.3.2.246 . ПМИД 31167308 . S2CID 34868087 .
Дальнейшее чтение
[ редактировать ]- Дж. Муди и К. Дж. Даркен, «Быстрое обучение в сетях локально настроенных процессоров», Neural Computation, 1, 281–294 (1989). Также см. Сети радиальных базисных функций согласно Муди и Даркену.
- Т. Поджо и Ф. Джирози, « Сети для аппроксимации и обучения », Proc. IEEE 78(9), 1484-1487 (1990).
- Роджер Д. Джонс , Ю.К. Ли, К.В. Барнс, Г.В. Флейк, К. Ли, П.С. Льюис и С. Цянь, Аппроксимация функций и прогнозирование временных рядов с помощью нейронных сетей , Материалы Международной совместной конференции по нейронным сетям, 17–21 июня , с. И-649 (1990 г.).
- Мартин Д. Буманн (2003). Радиальные базисные функции: теория и реализации . Кембриджский университет. ISBN 0-521-63338-9 .
- Йи, Пол В. и Хайкин, Саймон (2001). Регуляризованные радиальные базисные сети: теория и приложения . Джон Уайли. ISBN 0-471-35349-3 .
- Дэвис, Джон Р.; Коггешолл, Стивен В.; Джонс, Роджер Д .; Шутцер, Дэниел (1995). «Интеллектуальные системы безопасности». У Фридмана, Рой С.; Флейн, Роберт А.; Ледерман, Джесс (ред.). Искусственный интеллект на рынках капитала . Чикаго: Ирвин. ISBN 1-55738-811-3 .
- Саймон Хайкин (1999). Нейронные сети: комплексный фундамент (2-е изд.). Река Аппер-Сэдл, Нью-Джерси: Прентис-Холл. ISBN 0-13-908385-5 .
- С. Чен, К.Ф.Н. Коуэн и П.М. Грант, « Алгоритм обучения ортогональным методом наименьших квадратов для сетей с радиальными базисными функциями », Транзакции IEEE в нейронных сетях, том 2, № 2 (март) 1991 г.








![{\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i} \right\Vert {\big)} =\exp \left[-\beta _{i }\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/810b210447cf6a4e00b141425a5da1cf6cb3914c)




























![{\displaystyle e_{ij}={\begin{cases}a_{i},&{\mbox{if }}i\in [1,N]\\b_{ij},&{\mbox{if }} i\in [N+1,2N]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e69e7a0b20246396ad4ecf0619932d3818cb14fb)
![{\displaystyle v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big)}\ {\stackrel {\mathrm {def} }{=}}\ {\ begin{cases}\delta _{ij}\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox {if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)\rho {\big (}\left\Vert \mathbf {x} -\mathbf {c } _{i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6194ed23e27bf63b899a072ce2803f31fba1f84)
![{\displaystyle v_{ij}{\big (}\mathbf {x} -\mathbf {c} _{i}{\big)}\ {\stackrel {\mathrm {def} }{=}}\ {\ begin{cases}\delta _{ij}u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big )},&{\mbox{ if }}i\in [1,N]\\\left(x_{ij}-c_{ij}\right)u{\big (}\left\Vert \mathbf {x} -\mathbf {c} _ {i}\right\Vert {\big )},&{\mbox{if }}i\in [N+1,2N]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f7d20e63f94b312d972d1c925a999de68c68735)






![{\displaystyle K_{t}(\mathbf {w})\ {\stackrel {\mathrm {def} {=}}\ {\big [}y(t)-\varphi {\big (}\mathbf { x} (t),\mathbf {w} {\big )}{\big ]}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47c25fbbbb15c069216597e2a3489f0c7ba6ac62)








![{\displaystyle \left[{\begin{matrix}g_{11}&g_{12}&\cdots &g_{1N}\\g_{21}&g_{22}&\cdots &g_{2N}\\\vdots &&\ ddots &\vdots \\g_{N1}&g_{N2}&\cdots &g_{NN}\end{matrix}}\right]\left[{\begin{matrix}w_{1}\\w_{2}\ \\vdots \\w_{N}\end{matrix}}\right]=\left[{\begin{matrix}b_{1}\\b_{2}\\\vdots \\b_{N}\end {матрица}}\вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a4456b5dd861c3af9665875ed2e674003029074)









![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6ff0ca244dbf79403808304d1970f20cee63383)
![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big ) }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30d53a925c043711f42e74be811973f9c14563ea)
![{\displaystyle e_{ij}(t+1)=e_{ij}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}v_{ij}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ed23c9f1311d7090b1f9354acd1ea651133e87b)

![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}{\frac {\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\ Vert {\big )}}{\sum _{i=1}^{N}\rho ^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _ {i}\right\Vert {\big )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daada7fa66c0c152fa6ddbe9b4688bab0e069771)
![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}{\frac {u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right\Vert {\big )}}{\sum _{i=1}^{N}u^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i }\right\Vert {\big )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ded07d14fa15e102334231468d90bc62d88fba0e)
![{\displaystyle e_{ij}(t+1)=e_{ij}(t)+\nu {\big [}y(t)-\varphi {\big (}\mathbf {x} (t),\ mathbf {w} {\big )}{\big ]}{\frac {v_{ij}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )} }{\sum _{i=1}^{N}\sum _{j=1}^{n}v_{ij}^{2}{\big (}\mathbf {x} (t)-\mathbf {c} _{i}{\big )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca63b9d8b8402fb255847feee9f93cbedcfd71bd)
![{\displaystyle x(t+1)\ {\stackrel {\mathrm {def} {=}}\ f\left[x(t)\right]=4x(t)\left[1-x(t) \верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d18e751a88c7fd2ac285b21f9c567db55c214e97)
![{\displaystyle x(t+1)=f\left[x(t)\right]\approx \varphi (t)=\varphi \left[x(t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db59ba99d8c9e0d2e5d34cae9692a5f3a22cf33b)

![{\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i} \right\Vert {\big)} =\exp \left[-\beta _{i }\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]=\exp \left[-\beta _{i}\left(x(t )-c_{i}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c7d4d37abe3b8601a437cb4769cddc6cf3833e)

![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}x(t+1)-\varphi {\big (}\mathbf {x} (t) ,\mathbf {w} {\big )}{\big ]}{\frac {\rho {\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\ right\Vert {\big )}}{\sum _{i=1}^{N}\rho ^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c } _{i}\right\Vert {\big )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4fce40bfbe9b946581809f2a627f174aaf33c64)

![{\displaystyle \rho {\big (}\left\Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert {\big)} =\exp \left[-\beta \left\ Vert \mathbf {x} -\mathbf {c} _{i}\right\Vert ^{2}\right]=\exp \left[-\beta \left(x(t)-c_{i}\right )^{2}\вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b386dbd43b5eb5df76b52f6e6214f2b4339d4dae)
![{\displaystyle a_{i}(t+1)=a_{i}(t)+\nu {\big [}x(t+1)-\varphi {\big (}\mathbf {x} (t) ,\mathbf {w} {\big )}{\big ]}{\frac {u{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _{i}\right \Vert {\big )}}{\sum _{i=1}^{N}u^{2}{\big (}\left\Vert \mathbf {x} (t)-\mathbf {c} _ {i}\right\Vert {\big )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be34ccc983222e1bbeb72d63eab95e64393dceb0)


![{\displaystyle {x}(t+1)\approx \varphi (t)=\varphi [\varphi (t-1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ebe0e8d1ef472dc874ee8861bb9968afe83ad5a)
![{\displaystyle c[x(t),t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a43de76171d5e934b86617d2c4f31173f85f1943)
![{\displaystyle {x}_{}^{}(t+1)=4x(t)[1-x(t)]+c[x(t),t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff5cb6dda1ba3c7e3514d4472f64c4b2cd1ab18f)

![{\displaystyle c_{}^{}[x(t),t]\ {\stackrel {\mathrm {def} {=}}\ -\varphi [x(t)]+d(t+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e75069785f599ea18ae354ac38e34f625816011a)
![{\displaystyle y[x(t)]\approx f[x(t)]=x(t+1)-c[x(t),t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/398cd41f2ca68133f79c5f62a81068049fca98b8)

![{\displaystyle \varepsilon \ {\stackrel {\ mathrm {def} {=}} \ f[x(t)]-\varphi [x(t)]=x(t+1)-c[x(t) ),t]-\varphi [x(t)]=x(t+1)-d(t+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6acad5ff76bdcad25bf1beb62674724290392c10)