Параллельная внешняя память

В информатике модель параллельной внешней памяти (PEM) представляет собой с поддержкой кэша и внешней памятью абстрактную машину . ^[1] Это аналогия параллельных вычислений модели однопроцессорной внешней памяти (EM). Подобным образом, это аналогия с поддержкой кэша параллельной машины с произвольным доступом (PRAM). Модель PEM состоит из нескольких процессоров вместе с соответствующими частными кэшами и общей основной памятью.

Модель

Определение

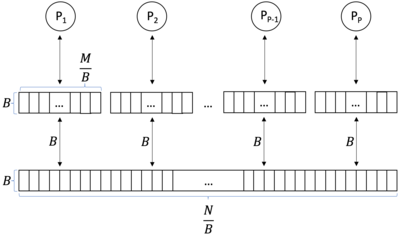
Модель PEM ^[1] представляет собой комбинацию модели EM и модели PRAM. Модель PEM — это вычислительная модель, состоящая из $P$ процессоры и двухуровневая иерархия памяти . Эта иерархия памяти состоит из большой внешней памяти (основной памяти) размером $N$ и $P$ небольшая внутренняя память (кеши) . Процессоры совместно используют основную память. Каждый кэш предназначен только для одного процессора. Процессор не может получить доступ к чужому кэшу. Тайники имеют размер $M$ который разделен на блоки размером $B$ . Процессоры могут выполнять операции только с данными, которые находятся в их кэше. Данные могут передаваться между основной памятью и кэшем блоками размером $B$ .

Сложность ввода-вывода

Мерой сложности модели PEM является сложность ввода-вывода, ^[1] который определяет количество параллельных передач блоков между основной памятью и кэшем. Во время параллельной передачи блоков каждый процессор может передать блок. Итак, если $P$ процессоры параллельно загружают блок данных размером $B$ формируют основную память в свои кэши, это считается сложностью ввода-вывода $O(1)$ нет $O(P)$ . Программа в модели PEM должна минимизировать передачу данных между основной памятью и кэшами и как можно больше оперировать данными в кэшах.

Конфликты чтения/записи

В модели PEM нет прямой сети связи между процессорами P. Процессоры должны взаимодействовать косвенно через основную память. Если несколько процессоров пытаются одновременно получить доступ к одному и тому же блоку в основной памяти, возникают конфликты чтения/записи. ^[1] происходить. Как и в модели PRAM, рассматриваются три различных варианта этой проблемы:

Одновременное чтение и параллельная запись (CRCW): один и тот же блок в основной памяти может одновременно читаться и записываться несколькими процессорами.
Параллельное чтение и эксклюзивная запись (CREW): один и тот же блок в основной памяти может одновременно читаться несколькими процессорами. Только один процессор может записывать данные в блок одновременно.
Эксклюзивное чтение Эксклюзивная запись (EREW): один и тот же блок в основной памяти не может быть прочитан или записан несколькими процессорами одновременно. Только один процессор может одновременно обращаться к блоку.

Следующие два алгоритма ^[1] решить проблему ЭКИПАЖА и ЭРВ, если $P\leq B$ процессоры записывают в один и тот же блок одновременно. Первый подход заключается в сериализации операций записи. Только один процессор за другим записывает в блок. В результате получается в общей сложности $P$ параллельные блочные передачи. Второй подход требует $O(\log(P))$ параллельная передача блоков и дополнительный блок для каждого процессора. Основная идея состоит в том, чтобы запланировать операции записи в виде двоичного дерева и постепенно объединить данные в один блок. В первом раунде $P$ процессоры объединяют свои блоки в $P/2$ блоки. Затем $P/2$ процессоры объединяют в себе $P/2$ блоки в $P/4$ . Эта процедура продолжается до тех пор, пока все данные не объединятся в один блок.

Сравнение с другими моделями


Модель	Многоядерный	Поддержка кэша
Машина произвольного доступа (ОЗУ)	Нет	Нет
Параллельная машина произвольного доступа (PRAM)	Да	Нет
Внешняя память (ЕМ)	Нет	Да
Параллельная внешняя память (PEM)	Да	Да

Примеры

Многостороннее разбиение

Позволять $M=\{m_{1},...,m_{d-1}\}$ быть вектором d-1 опорных точек, отсортированным в порядке возрастания. Пусть $A$ — неупорядоченное множество из N элементов. D-образный раздел ^[1] представляет собой $A$ множество $\Pi =\{A_{1},...,A_{d}\}$ , где $\cup _{i=1}^{d}A_{i}=A$ и $A_{i}\cap A_{j}=\emptyset$ для $1\leq i<j\leq d$ . $A_{i}$ называется i-м ведром. Количество элементов в $A_{i}$ больше, чем $m_{i-1}$ и меньше, чем $m_{i}^{2}$ . В следующем алгоритме ^[1] вход разделен на смежные сегменты размера N/P. $S_{1},...,S_{P}$ в основной памяти. Процессор i преимущественно работает на сегменте $S_{i}$ . Алгоритм многостороннего разбиения ( PEM_DIST_SORT^[1] PEM суммирования префиксов ) использует алгоритм ^[1] рассчитать сумму префикса с оптимальным $O\left({\frac {N}{PB}}+\log P\right)$ Сложность ввода-вывода. Этот алгоритм имитирует оптимальный алгоритм суммы префиксов PRAM.

// Compute parallelly a d-way partition on the data segments  $S_{i}$ 
for each processor i in parallel do
    Read the vector of pivots  $M$  into the cache.
    Partition  $S_{i}$  into d buckets and let vector  $M_{i}=\{j_{1}^{i},...,j_{d}^{i}\}$  be the number of items in each bucket.
end for

Run PEM prefix sum on the set of vectors  $\{M_{1},...,M_{P}\}$  simultaneously.

// Use the prefix sum vector to compute the final partition
for each processor i in parallel do
    Write elements  $S_{i}$  into memory locations offset appropriately by  $M_{i-1}$  and  $M_{i}$ .
end for

Using the prefix sums stored in  $M_{P}$  the last processor P calculates the vector  $B$  of bucket sizes and returns it.

Если вектор $d=O\left({\frac {M}{B}}\right)$ опорные точки M и входной набор A расположены в непрерывной памяти, то проблема d-стороннего разделения может быть решена в модели PEM с помощью $O\left({\frac {N}{PB}}+\left\lceil {\frac {d}{B}}\right\rceil >\log(P)+d\log(B)\right)$ Сложность ввода-вывода. Содержимое последних сегментов должно располагаться в непрерывной памяти.

Выбор

Задача выбора поиске k-го наименьшего элемента в неупорядоченном списке $A$ размера $N.$ заключается в Следующий код ^[1] использует PRAMSORT который представляет собой оптимальный алгоритм сортировки PRAM, который работает в $O(\log N)$ , и SELECT, который представляет собой алгоритм выбора оптимального для кэша однопроцессорного процессора.

if  $N\leq P$  then 
     ${\texttt {PRAMSORT}}(A,P)$ 
    return  $A[k]$ 
end if 

//Find median of each  $S_{i}$ 
for each processor  $i$  in parallel do 
     $m_{i}={\texttt {SELECT}}(S_{i},{\frac {N}{2P}})$ 
end for 

// Sort medians
 ${\texttt {PRAMSORT}}(\lbrace m_{1},\dots ,m_{2}\rbrace ,P)$ 

// Partition around median of medians
 $t={\texttt {PEMPARTITION}}(A,m_{P/2},P)$ 

if  $k\leq t$  then 
    return  ${\texttt {PEMSELECT}}(A[1:t],P,k)$ 
else 
    return  ${\texttt {PEMSELECT}}(A[t+1:N],P,k-t)$ 
end if

Предполагая, что входные данные хранятся в непрерывной памяти, PEMSELECT имеет сложность ввода-вывода:

O\left({\frac {N}{PB}}+\log(PB)\cdot \log({\frac {N}{P}})\right)

Сортировка распределения

Сортировка по распределению разделяет входной список $A$ размера $N$ на $d$ непересекающиеся сегменты одинакового размера. Затем каждый сегмент рекурсивно сортируется, и результаты объединяются в полностью отсортированный список.

Если $P=1$ задача делегируется оптимальному для кэша однопроцессорному алгоритму сортировки.

В противном случае следующий алгоритм ^[1] используется:

// Sample  ${\tfrac {4N}{\sqrt {d}}}$  elements from  $A$ 
for each processor  $i$  in parallel do
    if  $M<|S_{i}|$  then
         $d=M/B$ 
        Load  $S_{i}$  in  $M$ -sized pages and sort pages individually
    else
         $d=|S_{i}|$ 
        Load and sort  $S_{i}$  as single page
    end if
    Pick every  ${\sqrt {d}}/4$ 'th element from each sorted memory page into contiguous vector  $R^{i}$  of samples
end for 

in parallel do
    Combine vectors  $R^{1}\dots R^{P}$  into a single contiguous vector  ${\mathcal {R}}$ 
    Make  ${\sqrt {d}}$  copies of  ${\mathcal {R}}$ :  ${\mathcal {R}}_{1}\dots {\mathcal {R}}_{\sqrt {d}}$ 
end do

// Find  ${\sqrt {d}}$  pivots  ${\mathcal {M}}[j]$ 
for  $j=1$  to  ${\sqrt {d}}$  in parallel do
     ${\mathcal {M}}[j]={\texttt {PEMSELECT}}({\mathcal {R}}_{i},{\tfrac {P}{\sqrt {d}}},{\tfrac {j\cdot 4N}{d}})$ 
end for

Pack pivots in contiguous array  ${\mathcal {M}}$ 

// Partition  $A$ around pivots into buckets  ${\mathcal {B}}$ 
 ${\mathcal {B}}={\texttt {PEMMULTIPARTITION}}(A[1:N],{\mathcal {M}},{\sqrt {d}},P)$ 

// Recursively sort buckets
for  $j=1$  to  ${\sqrt {d}}+1$  in parallel do
    recursively call  ${\texttt {PEMDISTSORT}}$  on bucket  $j$ of size  ${\mathcal {B}}[j]$ 
    using  $O\left(\left\lceil {\tfrac {{\mathcal {B}}[j]}{N/P}}\right\rceil \right)$  processors responsible for elements in bucket  $j$ 
end for

Сложность ввода/вывода PEMDISTSORT является:

O\left(\left\lceil {\frac {N}{PB}}\right\rceil \left(\log _{d}P+\log _{M/B}{\frac {N}{PB}}\right)+f(N,P,d)\cdot \log _{d}P\right)

где

f(N,P,d)=O\left(\log {\frac {PB}{\sqrt {d}}}\log {\frac {N}{P}}+\left\lceil {\frac {\sqrt {d}}{B}}\log P+{\sqrt {d}}\log B\right\rceil \right)

Если выбрано такое количество процессоров $f(N,P,d)=O\left(\left\lceil {\tfrac {N}{PB}}\right\rceil \right)$ и $M<B^{O(1)}$ тогда сложность ввода-вывода составит:

$O\left({\frac {N}{PB}}\log _{M/B}{\frac {N}{B}}\right)$

Другие алгоритмы PEM


PEM-алгоритм	Сложность ввода-вывода	Ограничения
Сортировка слиянием ^[1]	$O\left({\frac {N}{PB}}\log _{\frac {M}{B}}{\frac {N}{B}}\right)={\textrm {sort}}_{P}(N)$	$P\leq {\frac {N}{B^{2}}},M=B^{O(1)}$
Рейтинг списка ^[2]	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {\frac {N/B^{2}}{\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}$
Эйлерова башня ^[2]	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {\frac {N}{B^{2}}},M=B^{O(1)}$
дерева выражений Оценка ^[2]	$O\left({\textrm {sort}}_{P}(N)\right)$	$P\leq {\frac {N}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}$
Поиск MST ^[2]	$O\left({\textrm {sort}}_{P}(\|V\|)+{\textrm {sort}}_{P}(\|E\|)\log {\tfrac {\|V\|}{pB}}\right)$	$p\leq {\frac {\|V\|+\|E\|}{B^{2}\log B\cdot \log ^{O(1)}N}},M=B^{O(1)}$

Где ${\textrm {sort}}_{P}(N)$ — это время, необходимое для сортировки $N$ элементов с помощью $P$ процессоров в модели PEM.

См. также

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Арге, Ларс; Гудрич, Майкл Т.; Нельсон, Майкл; Ситчинава, Нодари (2008). «Фундаментальные параллельные алгоритмы для мультипроцессоров с частным кэшем». Материалы двадцатого ежегодного симпозиума по параллелизму в алгоритмах и архитектурах . Нью-Йорк, Нью-Йорк, США: ACM Press. стр. 197–206. дои : 10.1145/1378533.1378573 . ISBN 9781595939739 . S2CID 11067041 .
^ Jump up to: ^а ^б ^с ^д Арге, Ларс; Гудрич, Майкл Т.; Ситчинава, Нодари (2010). «Алгоритмы параллельного графа внешней памяти». 2010 Международный симпозиум IEEE по параллельной и распределенной обработке (IPDPS) . IEEE. стр. 1–11. дои : 10.1109/ipdps.2010.5470440 . ISBN 9781424464425 . S2CID 587572 .

[:0-1] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л Арге, Ларс; Гудрич, Майкл Т.; Нельсон, Майкл; Ситчинава, Нодари (2008). «Фундаментальные параллельные алгоритмы для мультипроцессоров с частным кэшем». Материалы двадцатого ежегодного симпозиума по параллелизму в алгоритмах и архитектурах . Нью-Йорк, Нью-Йорк, США: ACM Press. стр. 197–206. дои : 10.1145/1378533.1378573 . ISBN 9781595939739 . S2CID 11067041 .

[:1-2] Jump up to: ^а ^б ^с ^д Арге, Ларс; Гудрич, Майкл Т.; Ситчинава, Нодари (2010). «Алгоритмы параллельного графа внешней памяти». 2010 Международный симпозиум IEEE по параллельной и распределенной обработке (IPDPS) . IEEE. стр. 1–11. дои : 10.1109/ipdps.2010.5470440 . ISBN 9781424464425 . S2CID 587572 .

[1]

[2]

v т и Параллельные вычисления
Общий	Распределенные вычисления Параллельные вычисления Массивная параллель Облачные вычисления Высокопроизводительные вычисления Многопроцессорность Многоядерный процессор ГПГПУ Компьютерная сеть Систолический массив
Уровни	Кусочек Инструкция Нить Задача Данные Память Петля Трубопровод
Многопоточность	Временной Одновременный (SMT) Одновременное и гетерогенное Спекулятивный (СпМТ) упреждающий Кооператив Кластерная многопоточная обработка (CMT) Аппаратный разведчик
Теория	Модель ПРАМ PEM-модели Анализ параллельных алгоритмов Закон Амдала Закон Густавсона Экономическая эффективность Метрика Карпа – Флатта Замедлять Ускорение
Элементы	Процесс Нить Волокно Окно инструкций Множество
Координация	Многопроцессорность Согласованность памяти Согласованность кэша Аннулирование кэша Барьер Синхронизация Контрольная точка приложения
Программирование	Потоковая обработка Программирование потоков данных Модели Неявный параллелизм Явный параллелизм Параллелизм Неблокирующий алгоритм
Аппаратное обеспечение	Таксономия Флинна СИСД SIMD Обработка массивов (SIMT) Конвейерная обработка Ассоциативная обработка МИСД МИМД Архитектура потока данных Конвейерный процессор Суперскалярный процессор Векторный процессор Мультипроцессор симметричный асимметричный Память общий распределенный распределенный общий ОДИН НУМА ЕСТЬ Массивно-параллельный компьютер Компьютерный кластер Кластер Беовульф Сетевой компьютер Аппаратное ускорение
API	Атеджи ПХ Способствовать росту Часовня HPX Очарование++ Том Коаррей Фортран ДРУГОЙ Дриада С++ AMP Глобальные массивы GPUОткрыть ИМБ OpenMP OpenCL OpenHMPP OpenACC Параллельные расширения НДС pthreads РафтЛиб РПЦм СКП TBB ЗПЛ
Проблемы	Автоматическое распараллеливание Тупик Детерминированный алгоритм Смущающе параллельно Параллельное замедление Состояние гонки Программная блокировка Масштабируемость Голод
Категория: Параллельные вычисления