Плазменные колебания

Плазменные колебания , также известные как волны Ленгмюра (в честь Ирвинга Ленгмюра ), представляют собой быстрые колебания электронной плотности в проводящих средах, таких как плазма или металлы, в ультрафиолетовой области. Колебания можно описать как нестабильность диэлектрической функции газа свободных электронов . Частота слабо зависит от длины волны колебания. Квазичастица , возникающая в результате квантования этих колебаний, является плазмоном .

Волны Ленгмюра были открыты американскими физиками Ирвингом Ленгмюром и Льюи Тонксом в 1920-х годах. По форме они параллельны волнам неустойчивости Джинса , вызванным гравитационными неустойчивостями в статической среде.

Механизм

Рассмотрим электрически нейтральную плазму в равновесии, состоящую из газа положительно заряженных ионов и отрицательно заряженных электронов . Если сместить на небольшую величину электрон или группу электронов относительно ионов, кулоновская сила притянет электроны назад, действуя как восстанавливающая сила.

«Холодные» электроны

Если пренебречь тепловым движением электронов, то можно показать, что плотность заряда колеблется с плазменной частотой

$\omega _{\mathrm {pe} }={\sqrt {\frac {n_{\mathrm {e} }e^{2}}{m^{*}\varepsilon _{0}}}},\left[\mathrm {rad/s} \right]$ ( единицы СИ ),

$\omega _{\mathrm {pe} }={\sqrt {\frac {4\pi n_{\mathrm {e} }e^{2}}{m^{*}}}},\left[\mathrm {rad/s} \right]$ ( единицы СГС ),

где $n_{\mathrm {e} }$ - плотность электронов, $e$ электрический заряд , $m^{*}$ - эффективная масса электрона, а $\varepsilon _{0}$ - диэлектрическая проницаемость свободного пространства . Обратите внимание, что приведенная выше формула получена в приближении бесконечности массы иона. Обычно это хорошее приближение, поскольку электроны намного легче ионов.

Доказательство с использованием уравнений Максвелла. Предполагая колебания плотности заряда $\rho (\omega )=\rho _{0}e^{-i\omega t}$ уравнение неразрывности:

$$\nabla \cdot \mathbf {j} =-{\frac {\partial \rho }{\partial t}}=i\omega \rho (\omega )$$

закон Гаусса

$$\nabla \cdot \mathbf {E} (\omega )=4\pi \rho (\omega )$$

и проводимость

$$\mathbf {j} (\omega )=\sigma (\omega )\mathbf {E} (\omega )$$

взяв расхождения с обеих сторон и подставив приведенные выше соотношения:

$$i\omega \rho (\omega )=4\pi \sigma (\omega )\rho (\omega )$$

что всегда верно, только если

$$1+{\frac {4\pi i\sigma (\omega )}{\omega }}=0$$

Но это еще и диэлектрическая проницаемость (см. Модель Друде ) $\epsilon (\omega )=1+{\frac {4\pi i\sigma (\omega )}{\omega }}$и условие прозрачности (т.е. $\epsilon \geq 0$ от определенной плазменной частоты $\omega _{\rm {p}}$ и выше), здесь то же самое условие $\epsilon =0$ применяются, чтобы сделать возможным также распространение волн плотности в плотности заряда.

Это выражение необходимо видоизменить в случае электрон- позитронной плазмы часто встречающейся в астрофизике . Поскольку частота не зависит от длины волны , эти колебания имеют бесконечную фазовую скорость и нулевую групповую скорость .

Обратите внимание, что когда $m^{*}=m_{\mathrm {e} }$, плазменная частота, $\omega _{\mathrm {pe} }$, зависит только от физических констант и плотности электронов $n_{\mathrm {e} }$. Числовое выражение для угловой плазменной частоты:

$$f_{\text{pe}}={\frac {\omega _{\text{pe}}}{2\pi }}~\left[{\text{Hz}}\right]$$

Металлы прозрачны только для света с частотой выше плазменной частоты металла. Для типичных металлов, таких как алюминий или серебро, $n_{\mathrm {e} }$ примерно 10 ²³ см ⁻³ , что переносит плазменную частоту в ультрафиолетовую область. Вот почему большинство металлов отражают видимый свет и кажутся блестящими.

«Тёплые» электроны

Когда эффекты электронов тепловой скорости ${\textstyle v_{\mathrm {e,th} }={\sqrt {k_{\mathrm {B} }T_{\mathrm {e} }/m_{\mathrm {e} }}}}$ Принимая во внимание, давление электронов действует как восстанавливающая сила, а электрическое поле и колебания распространяются с частотой и волновым числом, связанными продольным ленгмюровским числом волна:

$$\omega ^{2}=\omega _{\mathrm {pe} }^{2}+{\frac {3k_{\mathrm {B} }T_{\mathrm {e} }}{m_{\mathrm {e} }}}k^{2}=\omega _{\mathrm {pe} }^{2}+3k^{2}v_{\mathrm {e,th} }^{2},$$

называется Бома – Гросса дисперсионным соотношением . Если пространственный масштаб велик по сравнению с длиной Дебая , колебания лишь слабо модифицируются членом давления , но на малых масштабах член давления доминирует, и волны становятся бездисперсионными со скоростью ${\sqrt {3}}\cdot v_{\mathrm {e,th} }$. Однако для таких волн тепловая скорость электронов сравнима с фазовой скоростью , т. е.

$$v\sim v_{\mathrm {ph} }\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\omega }{k}},$$

поэтому плазменные волны могут ускорять электроны, движущиеся со скоростью, почти равной фазовой скорости волны. Этот процесс часто приводит к форме бесстолкновительного демпфирования, называемой демпфированием Ландау . Следовательно, часть с большим k в дисперсионном уравнении трудно наблюдать и она редко имеет последствия.

В ограниченной плазме краевые электрические поля могут приводить к распространению плазменных колебаний, даже когда электроны холодные.

В металле или полупроводнике влияние периодического потенциала ионов необходимо учитывать электронов . Обычно это делается с использованием эффективной массы вместо m .

Плазменные колебания и эффект отрицательной массы

Рисунок 1. Ядро с массой $m_{2}$ соединяется внутри через пружину с $k_{2}$ к оболочке с массой $m_{1}$. На систему действует синусоидальная сила $F(t)={\widehat {F}}\sin \omega t$.

Плазменные колебания могут вызвать эффект « отрицательной массы ». Механическая модель, вызывающая эффект отрицательной эффективной массы, изображена на рисунке 1 . Ядро с массой $m_{2}$ соединен внутри через пружину с постоянным $k_{2}$ к оболочке с массой $m_{1}$. На систему действует внешняя синусоидальная сила. $F(t)={\widehat {F}}\sin \omega t$. Если решить уравнения движения масс $m_{1}$ и $m_{2}$ и заменить всю систему единой эффективной массой $m_{\rm {eff}}$ мы получаем:

$$m_{\rm {eff}}=m_{1}+{m_{2}\omega _{0}^{2} \over \omega _{0}^{2}-\omega ^{2}},$$

где ${\textstyle \omega _{0}={\sqrt {k_{2}/m_{2}}}}$. Когда частота $\omega$ подходы $\omega _{0}$ сверху эффективная масса $m_{\rm {eff}}$ будет отрицательным.

Рисунок 2. Газ со свободными электронами $m_{2}$ встроен в ионную решетку $m_{1}$; $\omega _{\rm {p}}$ – плазменная частота (левый рисунок). Эквивалентная механическая схема системы (правый эскиз).

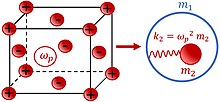
Отрицательная эффективная масса (плотность) также становится возможной на основе электромеханической связи, использующей плазменные колебания газа свободных электронов (см. Рисунок 2 ). Отрицательная масса появляется в результате вибрации металлической частицы с частотой $\omega$ что близко к частоте плазменных колебаний электронного газа $m_{2}$ относительно ионной решетки $m_{1}$. Плазменные колебания представлены упругой пружиной $k_{2}=\omega _{\rm {p}}^{2}m_{2}$, где $\omega _{\rm {p}}$ — плазменная частота. Таким образом, металлическая частица, колеблющаяся с внешней частотой ω, описывается эффективной массой

$$m_{\rm {eff}}=m_{1}+{m_{2}\omega _{\rm {p}}^{2} \over \omega _{\rm {p}}^{2}-\omega ^{2}},$$

что отрицательно, когда частота $\omega$ подходы $\omega _{\rm {p}}$ сверху. Сообщалось о метаматериалах, использующих эффект отрицательной массы вблизи плазменной частоты.

См. также

• Электронный след
• Плазмон
• Релятивистская квантовая химия
• Поверхностный плазмонный резонанс
• Верхнее гибридное колебание , в частности для обсуждения модификации режима при углах распространения, наклоненных к магнитному полю.
• Волны в плазме

Дальнейшее чтение

• Лонгэйр, Малкольм С. (1998), Формирование галактики , Берлин: Springer, ISBN  978-3-540-63785-1