Уравнение акустической волны

В физике уравнение акустической волны второго порядка представляет собой уравнение в частных производных , которое управляет распространением акустических волн через материальную среду, соответственно. поле стоячей волны . Уравнение описывает эволюцию акустического давления p или скорости частицы u в зависимости от положения x и времени t . Упрощенная (скалярная) форма уравнения описывает акустические волны только в одном пространственном измерении, тогда как более общая форма описывает волны в трех измерениях. Волны, распространяющиеся в заранее заданном направлении, также можно рассчитать с помощью одностороннего волнового уравнения первого порядка .

Для сред с потерями необходимо применять более сложные модели, чтобы учесть частотно-зависимое затухание и фазовую скорость. Такие модели включают уравнения акустических волн, которые включают дробные производные , см. также статью об акустическом затухании или обзорный документ.

В одном измерении

Уравнение

Волновое уравнение, описывающее поле стоячей волны в одном измерении (положение $x$) является

${\partial ^{2}p \over \partial x^{2}}-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0,$

где $p$ – акустическое давление (локальное отклонение от давления окружающей среды), где $c$ это скорость звука .

Решение

При условии, что скорость $c$ — константа, не зависящая от частоты (бездисперсионный случай), то наиболее общее решение имеет вид

$p=f(ct-x)+g(ct+x)$

где $f$ и $g$ — любые две дважды дифференцируемые функции. Это можно представить как суперпозицию двух сигналов произвольного профиля, одного ( $f$), перемещаясь вверх по оси X, а другая ( $g$) вниз по оси X со скоростью $c$. Частный случай синусоидальной волны, бегущей в одном направлении, получается выбором либо $f$ или $g$ быть синусоидой, а другой - нулем, что дает

$p=p_{0}\sin(\omega t\mp kx)$.

где $\omega$ - угловая частота волны и $k$ это его волновое число .

Вывод

Вывод уравнения акустической волны

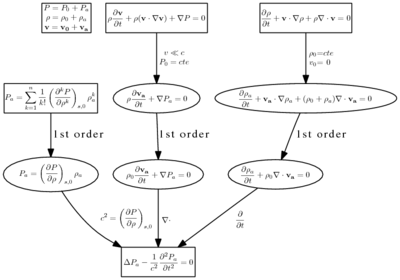
Вывод волнового уравнения включает три этапа: вывод уравнения состояния, линеаризованного одномерного уравнения неразрывности и линеаризованного одномерного уравнения силы.

Уравнение состояния ( закон идеального газа )

$PV=nRT$

В адиабатическом процессе давление P как функция плотности $\rho$ может быть линеаризовано до

$P=C\rho \,$

где C — некоторая константа. Разбив давление и плотность на их средние и полные компоненты и отметив, что $C={\frac {\partial P}{\partial \rho }}$:

$P-P_{0}=\left({\frac {\partial P}{\partial \rho }}\right)(\rho -\rho _{0})$.

Адиабатический модуль объемного сжатия жидкости определяется как

$B=\rho _{0}\left({\frac {\partial P}{\partial \rho }}\right)_{adiabatic}$

что дает результат

$P-P_{0}=B{\frac {\rho -\rho _{0}}{\rho _{0}}}$.

Конденсация s определяется как изменение плотности при заданной плотности окружающей среды.

$s={\frac {\rho -\rho _{0}}{\rho _{0}}}$

Линеаризованное уравнение состояния принимает вид

$p=Bs\,$ где p — акустическое давление ( $P-P_{0}$).

Уравнение неразрывности (сохранения массы) в одном измерении имеет вид

${\frac {\partial \rho }{\partial t}}+{\frac {\partial }{\partial x}}(\rho u)=0$.

Где u — скорость потока жидкости.Опять же, уравнение необходимо линеаризовать, а переменные разделить на средние и переменные компоненты.

${\frac {\partial }{\partial t}}(\rho _{0}+\rho _{0}s)+{\frac {\partial }{\partial x}}(\rho _{0}u+\rho _{0}su)=0$

Переставляя местами и отмечая, что плотность окружающей среды не меняется ни во времени, ни в положении и что конденсация, умноженная на скорость, представляет собой очень небольшое число:

${\frac {\partial s}{\partial t}}+{\frac {\partial }{\partial x}}u=0$

Уравнение силы Эйлера (сохранение импульса) — последний необходимый компонент. В одном измерении уравнение имеет вид:

$\rho {\frac {Du}{Dt}}+{\frac {\partial P}{\partial x}}=0$,

где $D/Dt$ представляет собой конвективную, субстанциональную или материальную производную , которая является производной в точке, движущейся вместе со средой, а не в фиксированной точке.

Линеаризация переменных:

$(\rho _{0}+\rho _{0}s)\left({\frac {\partial }{\partial t}}+u{\frac {\partial }{\partial x}}\right)u+{\frac {\partial }{\partial x}}(P_{0}+p)=0$.

После перестановки и пренебрежения малыми членами полученное уравнение становится линеаризованным одномерным уравнением Эйлера:

$\rho _{0}{\frac {\partial u}{\partial t}}+{\frac {\partial p}{\partial x}}=0$.

Взятие производной по времени уравнения неразрывности и пространственной производной уравнения силы приводит к:

${\frac {\partial ^{2}s}{\partial t^{2}}}+{\frac {\partial ^{2}u}{\partial x\partial t}}=0$

$\rho _{0}{\frac {\partial ^{2}u}{\partial x\partial t}}+{\frac {\partial ^{2}p}{\partial x^{2}}}=0$.

Умножив первое на $\rho _{0}$, вычитая эти два и подставляя линеаризованное уравнение состояния,

$-{\frac {\rho _{0}}{B}}{\frac {\partial ^{2}p}{\partial t^{2}}}+{\frac {\partial ^{2}p}{\partial x^{2}}}=0$.

Конечный результат

${\partial ^{2}p \over \partial x^{2}}-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0$

где $c={\sqrt {\frac {B}{\rho _{0}}}}$ это скорость распространения.

В трёх измерениях

Уравнение

Фейнман обеспечивает вывод волнового уравнения для звука в трех измерениях как

$\nabla ^{2}p-{1 \over c^{2}}{\partial ^{2}p \over \partial t^{2}}=0,$

где $\nabla ^{2}$ – оператор Лапласа , $p$ – акустическое давление (локальное отклонение от давления окружающей среды), $c$ это скорость звука .

Аналогичное волновое уравнение, но для векторного поля, скорости частицы имеет вид

$\nabla ^{2}\mathbf {u} \;-{1 \over c^{2}}{\partial ^{2}\mathbf {u} \; \over \partial t^{2}}=0$.

В некоторых ситуациях удобнее решать волновое уравнение для абстрактного скалярного потенциала скорости поля , имеющего вид

$\nabla ^{2}\Phi -{1 \over c^{2}}{\partial ^{2}\Phi \over \partial t^{2}}=0$

а затем вывести физические величины: скорость частицы и акустическое давление по уравнениям (или определению, в случае скорости частицы):

$\mathbf {u} =\nabla \Phi \;$,

$p=-\rho {\partial \over \partial t}\Phi$.

Решение

Следующие решения получены разделением переменных в разных системах координат. Это векторные решения, то есть они имеют неявный коэффициент зависимости от времени $e^{i\omega t}$ где $\omega =2\pi f$ - угловая частота . Явная зависимость от времени определяется выражением

$p(r,t,k)=\operatorname {Real} \left[p(r,k)e^{i\omega t}\right]$

Здесь $k=\omega /c\$ это волновое число .

Декартовы координаты

$p(r,k)=Ae^{\pm ikr}$.

Цилиндрические координаты

$p(r,k)=AH_{0}^{(1)}(kr)+\ BH_{0}^{(2)}(kr)$.

где асимптотические приближения к функциям Ганкеля , когда $kr\rightarrow \infty$, являются

$H_{0}^{(1)}(kr)\simeq {\sqrt {\frac {2}{\pi kr}}}e^{i(kr-\pi /4)}$

$H_{0}^{(2)}(kr)\simeq {\sqrt {\frac {2}{\pi kr}}}e^{-i(kr-\pi /4)}$.

Сферические координаты

$p(r,k)={\frac {A}{r}}e^{\pm ikr}$.

В зависимости от выбранного соглашения Фурье один из них представляет собой бегущую наружу волну, а другой - нефизическую бегущую внутрь волну. Волна решения, бегущая внутрь, нефизична только из-за сингулярности, возникающей при r = 0; внутренние бегущие волны действительно существуют.

См. также

• Акустика
• Акустическое затухание
• Акустическая теория
• Волновое уравнение
• Одностороннее волновое уравнение
• Дифференциальные уравнения
• Термодинамика
• Гидродинамика
• Давление
• Закон идеального газа