Функция Бесселя

Функции Бесселя , впервые определенные математиком Даниэлем Бернулли , а затем обобщенные Фридрихом Бесселем , являются каноническими решениями y ( x ) Бесселя. дифференциального уравнения
Наиболее важными являются случаи, когда является целым или полуцелым числом . Функции Бесселя для целых чисел также известны как цилиндрические функции или цилиндрические гармоники , поскольку они появляются в решении уравнения Лапласа в цилиндрических координатах . Сферические функции Бесселя с полуцелыми числами получаются при решении уравнения Гельмгольца в сферических координатах .
Приложения функций Бесселя [ править ]
Уравнение Бесселя возникает при нахождении разделимых решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических или сферических координатах . Поэтому функции Бесселя особенно важны для многих задач распространения волн и статических потенциалов. При решении задач в цилиндрических системах координат получаются функции Бесселя целого порядка ( α = n ); в сферических задачах получают полуцелые порядки ( α = n + 1/2 ) . Например:
- Электромагнитные волны в цилиндрическом волноводе
- Амплитуды давления невязких вращательных течений
- Теплопроводность в цилиндрическом объекте
- Режимы вибрации тонкой круглой или кольцевой акустической мембраны (например, пластика барабана или другого мембранофона ) или более толстых пластин, таких как листовой металл (см. Теорию пластин Кирхгофа – Лява , Теорию пластин Миндлина – Рейсснера )
- Проблемы диффузии на решетке
- Решения радиального уравнения Шрёдингера (в сферических и цилиндрических координатах) для свободной частицы
- Представление фейнмановского пропагатора в квантовой теории поля в позиционном пространстве
- Определение закономерностей акустического излучения
- Частотно-зависимое трение в кольцевых трубопроводах
- Динамика плавающих тел
- Угловое разрешение
- Дифракция от спиральных объектов, включая ДНК
- Функция плотности вероятности произведения двух нормально распределенных случайных величин [1]
- Анализ поверхностных волн, генерируемых микротреморами, в геофизике и сейсмологии .
Функции Бесселя появляются и в других задачах, таких как обработка сигналов (например, см. синтез FM-звука , окно Кайзера или фильтр Бесселя ).
Определения [ править ]
Поскольку это линейное дифференциальное уравнение, решения можно масштабировать до любой амплитуды. Амплитуды, выбранные для функций, взяты из ранних работ, в которых функции появлялись как решения определенных интегралов, а не как решения дифференциальных уравнений. Поскольку дифференциальное уравнение имеет второй порядок, должно быть два линейно независимых решения. Однако в зависимости от обстоятельств удобны различные рецептуры этих растворов. Различные варианты обобщены в таблице ниже и описаны в следующих разделах.
| Тип | Первый вид | Второй вид |
|---|---|---|
| Функции Бесселя | Дж а | Да |
| Модифицированные функции Бесселя | я α | К α |
| Функции Ханкеля | ЧАС (1) α = J α + iY α | ЧАС (2) α = J α − iY α |
| Сферические функции Бесселя | дж н | затем |
| Сферические функции Ханкеля | час (1) п = j n + iy n | час (2) п = j n - iy n |
рода иногда обозначаются N n и nn n соответственно, а не Y n и y Функции Бесселя второго рода и сферические функции Бесселя второго . [2] [3]
Функции Бесселя первого рода: J α [ править ]
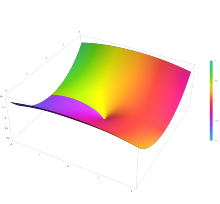

Функции Бесселя первого рода, обозначаемые как J α ( x ) , являются решениями дифференциального уравнения Бесселя. Для целого или положительного α функции Бесселя первого рода конечны в начале координат ( x = 0 ); в то время как для отрицательных нецелых α функции Бесселя первого рода расходятся при приближении x к нулю. Определить функцию можно с помощью раз ряд Маклорена (обратите внимание, что α не обязательно должно быть целым числом, а нецелые степени не допускаются в ряду Тейлора), который можно найти, применив метод Фробениуса к уравнению Бесселя: [4]
Для нецелого числа α функции J α ( x ) и J − α ( x ) линейно независимы и, следовательно, являются двумя решениями дифференциального уравнения. С другой стороны, для целого порядка n справедливо следующее соотношение (гамма-функция имеет простые полюса для каждого из неположительных целых чисел): [5]
Это означает, что два решения больше не являются линейно независимыми. В этом случае второе линейно независимое решение оказывается функцией Бесселя второго рода, как обсуждается ниже.
Интегралы Бесселя [ править ]
Другое определение функции Бесселя для целочисленных значений n возможно с использованием интегрального представления: [6]
Именно такой подход использовал Бессель. [8] и из этого определения он вывел несколько свойств функции. Определение может быть расширено до нецелых порядков с помощью одного из интегралов Шлефли для Re( x ) > 0 : [6] [9] [10] [11] [12]
Связь с гипергеометрическим рядом [ править ]
Функции Бесселя можно выразить через обобщенный гипергеометрический ряд следующим образом: [13]
Это выражение связано с развитием функций Бесселя через функцию Бесселя–Клиффорда .
с Лагерра Связь полиномами
Через полиномы Лагерра L k и произвольно выбранный параметр t функцию Бесселя можно выразить как [14]
Функции Бесселя второго рода: Y α [ править ]

Функции Бесселя второго рода, обозначаемые Y α ( x ) , иногда обозначаемые вместо этого N α ( x ) , являются решениями дифференциального уравнения Бесселя, имеющими особенность в начале координат ( x = 0 ) и многозначными . Их иногда называют функциями Вебера , так как они были введены Х. М. Вебером ( 1873 ), а также функциями Неймана после Карла Неймана . [15]
Для нецелого числа Y α α ( x ) связано с J α ( x ) соотношением
В случае целочисленного порядка n функция определяется путем достижения предела, когда нецелое значение α стремится к n :
Если n — целое неотрицательное число, мы имеем ряд [16]

где — дигамма-функция , логарифмическая производная гамма -функции . [17]
Существует также соответствующая интегральная формула (для Re( x ) > 0 ): [18]
В случае, когда n = 0 ,
Y α ( x ) необходим как второе линейно независимое решение уравнения Бесселя, когда α является целым числом. Но Y α ( x ) имеет большее значение. Его можно рассматривать как «естественного» партнера J α ( x ) . См. также подраздел о функциях Ханкеля ниже.
Более того, когда α — целое число, как и в случае с функциями первого рода, справедливо следующее соотношение:
И J α ( x ) , и Y α ( x ) являются голоморфными функциями на x комплексной плоскости, разрезанной вдоль отрицательной вещественной оси. Когда α является целым числом, функции Бесселя являются целыми функциями x J . Если x зафиксирован на ненулевом значении, то функции Бесселя являются целыми функциями от α .
Функции Бесселя второго рода, когда α — целое число, являются примером решения второго рода в теореме Фукса .
Функции Ханкеля: H (1)
а , ч (2)
а [ править ]

n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i
Другой важной формулировкой двух линейно независимых решений уравнения Бесселя являются функции Ганкеля первого и второго рода , H (1)
α ( x ) и H (2)
α ( x ) , определяемый как [19]
где я — мнимая единица . Эти линейные комбинации известны также как функции Бесселя третьего рода ; это два линейно независимых решения дифференциального уравнения Бесселя. Они названы в честь Германа Ханкеля .
Эти формы линейной комбинации удовлетворяют многочисленным простым на вид свойствам, таким как асимптотические формулы или интегральные представления. Здесь «простой» означает появление множителя вида e я ж (х) . Серьезно где , вещественны, функции Бесселя первого и второго рода представляют собой действительную и мнимую части соответственно первой функции Ганкеля и вещественную и отрицательную мнимую части второй функции Ганкеля. Таким образом, приведенные выше формулы являются аналогами формулы Эйлера с заменой H (1)
а ( Икс ) , Ч (2)
α ( x ) для и , для , , как явно показано в асимптотическом разложении .
Функции Ханкеля используются для выражения цилиндрических волновых решений уравнения цилиндрических волн, распространяющихся наружу и внутрь, соответственно (или наоборот, в зависимости от соглашения о знаках для частоты ).
Используя предыдущие соотношения, их можно выразить как
Если α является целым числом, необходимо вычислить предел. Следующие отношения действительны независимо от того, является ли α целым числом или нет: [20]
В частности, если α = m + 1 / 2 , где m — неотрицательное целое число, из приведенных выше соотношений прямо следует, что
Они полезны при разработке сферических функций Бесселя (см. ниже).
Функции Ханкеля допускают следующие интегральные представления для Re( x ) > 0 : [21]
Модифицированные функции Бесселя: I α , K α [ править ]
Функции Бесселя действительны даже для комплексных аргументов x , а важным частным случаем является случай чисто мнимого аргумента. В этом случае решения уравнения Бесселя называются модифицированными функциями Бесселя (или иногда гиперболическими функциями Бесселя ) первого и второго рода и определяются как [22]
может быть выражено через функции Ганкеля:
Используя эти две формулы, получим результат + , широко известный как интеграл Николсона или формула Николсона, можно получить следующим образом:
при условии, что условие Re( x ) > 0 выполнено. Также можно показать, что
только тогда, когда | Ре(α) | < 1/2 , = и Re(x) ≥ 0 но не тогда, когда x 0 . [23]
Мы можем выразить первую и вторую функции Бесселя через модифицированные функции Бесселя (они справедливы, если − π < arg z ≤ п / 2 ): [24]
I α ( x ) и K α ( x ) — два линейно независимых решения модифицированного уравнения Бесселя : [25]
В отличие от обычных функций Бесселя, которые колеблются как функции действительного аргумента, I α и K α являются экспоненциально растущими и убывающими функциями соответственно. обычная функция Бесселя Jα и , функция Iα Как и обращается в ноль при x = 0 при α > 0 конечна при x = 0 при α = 0 . Аналогично, K α расходится в точке x = 0 с особенностью логарифмического типа для K 0 , и 1/2 а ) С(| | (2/ х ) | а | в противном случае. [26]
 |  |
Две интегральные формулы для модифицированных функций Бесселя: (для Re( x ) > 0 ): [27]
Функции Бесселя можно описать как преобразования Фурье степеней квадратичных функций. Например (для Re(ω) > 0 ):
Это можно доказать, показав равенство приведенному выше интегральному определению для K 0 . Это делается путем интегрирования замкнутой кривой в первом квадранте комплексной плоскости.
Модифицированные функции Бесселя K 1/3 и K 2/3 могут быть представлены в виде быстро сходящихся интегралов. [28]
Модифицированная функция Бесселя полезно представить распределение Лапласа как смесь нормальных распределений в экспоненциальном масштабе.
Модифицированную функцию Бесселя второго рода также называли следующими именами (ныне редкими):
- Функция бассета в честь Альфреда Барнарда Бассета
- Модифицированная функция Бесселя третьего рода.
- Модифицированная функция Ханкеля [29]
- Функция Макдональда после Гектора Манро Макдональда
Сферические функции Бесселя: j n , y n [ править ]

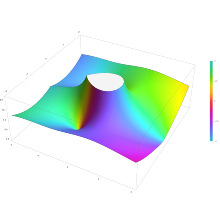


При решении уравнения Гельмгольца в сферических координатах методом разделения переменных радиальное уравнение имеет вид
Два линейно независимых решения этого уравнения называются сферическими функциями Бесселя j n и y n и связаны с обычными функциями Бесселя J n и Y n соотношением [30]
y n обозначается nn η или n ; также некоторые авторы называют эти функции сферическими функциями Неймана .
Из связей с обычными функциями Бесселя непосредственно видно, что:
Сферические функции Бесселя также можно записать в виде ( формулы Рэлея ) [31]
Нулевая сферическая функция Бесселя j 0 ( x ) также известна как (ненормированная) функция sinc . Первые несколько сферических функций Бесселя: [32]
Генерирующая функция [ править ]
Сферические функции Бесселя имеют производящие функции [34]
Разложения в конечные ряды [ править ]
В отличие от целочисленных функций Бесселя J n ( x ), Y n ( x ) , сферические функции Бесселя j n ( x ), y n ( x ) имеют выражение в виде конечного ряда: [35]
Дифференциальные отношения [ править ]
В дальнейшем f n представляет собой любое из j n , y n , h (1)
п , ч (2)
n для n = 0, ±1, ±2, ... [36]
Сферические функции Ханкеля: h (1)
п , ч (2)
н [ править ]

n ( x ) с n = -0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i

n ( x ) с n = −0,5 в комплексной плоскости от −2 − 2 i до 2 + 2 i
Существуют также сферические аналоги функций Ганкеля :
Фактически, существуют простые выражения в замкнутой форме для функций Бесселя полуцелого порядка через стандартные тригонометрические функции и, следовательно, для сферических функций Бесселя. В частности, для неотрицательных целых чисел n :
и ч (2)
n является его комплексно-сопряженным числом (для вещественного x ). Отсюда, например, следует, что j 0 ( x ) = грех x / x и y 0 ( x ) знак равно - cos x / x и так далее.
Сферические функции Ханкеля появляются в задачах, связанных с распространением сферических волн , например, в мультипольном разложении электромагнитного поля .
Функции Риккати–Бесселя: S n , C n , ξ n , ζ n [ править ]
Функции Риккати – Бесселя лишь незначительно отличаются от сферических функций Бесселя:
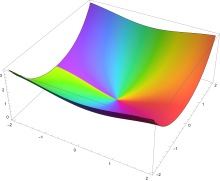
Они удовлетворяют дифференциальному уравнению
Например, такого рода дифференциальное уравнение появляется в квантовой механике при решении радиальной составляющей уравнения Шредингера с гипотетическим цилиндрическим бесконечным потенциальным барьером. [37] Это дифференциальное уравнение и решения Риккати-Бесселя также возникают в задаче рассеяния электромагнитных волн сферой, известной как рассеяние Ми после первого опубликованного решения Ми (1908). См., например, Ду (2004). [38] для последних разработок и ссылок.
Следуя Дебаю , обозначения ψn , Cn χn ( используются вместо Sn , ) иногда 1909 .
формы Асимптотические
Функции Бесселя имеют следующие асимптотики . Для мелких споров , получается, когда не является отрицательным целым числом: [4]
Когда α является отрицательным целым числом, мы имеем
Для функции Бесселя второго рода имеем три случая:
Для больших действительных аргументов z ≫ | α 2 − 1 / 4 | , невозможно написать истинную асимптотическую форму для функций Бесселя первого и второго рода (если только α не является полуцелым ), потому что они имеют нули вплоть до бесконечности, что должно быть точно сопоставлено любым асимптотическим разложением. Однако для заданного значения arg z можно написать уравнение, содержащее член порядка | г | −1 : [39]
(Для α = 1/2 последних членов в ; этих формулах выпадают полностью см. сферические функции Бесселя выше.)
Асимптотики функций Ганкеля:
Их можно распространить на другие значения arg z, используя уравнения, связывающие H (1)
α ( зе я π ) и Ч (2)
α ( зе я π ) до Ч (1)
α ( z ) и Ч (2)
α ( z ) . [40]
Интересно, что хотя функция Бесселя первого рода является средним из двух функций Ганкеля, J α ( z ) не является асимптотической по отношению к среднему из этих двух асимптотических форм, когда z отрицательно (поскольку ни одна, ни другая не будет там правильно, в зависимости от используемого аргумента z ). Но асимптотики функций Ханкеля позволяют записать асимптотики функций Бесселя первого и второго рода для комплексных (невещественных) z при условии, что | г | стремится к бесконечности при постоянном фазовом угле arg z (с использованием квадратного корня, имеющего положительную действительную часть):
Для модифицированных функций Бесселя Ханкель разработал асимптотические (большие аргументы) разложения : также [41] [42]
Существует также асимптотическая форма (для больших действительных ) [43]
Когда α = 1/2 мы имеем , все члены, кроме первого, обращаются в нуль, и
Для мелких споров , у нас есть
Свойства [ править ]
Для целочисленного порядка α = n : J n часто определяется через ряд Лорана для производящей функции
Бесконечный ряд функций Бесселя в виде где возникают во многих физических системах и в замкнутой форме определяются рядом Суна. [44] Например, когда N = 3: . В более общем смысле ряд Сунга и чередующийся ряд Сунга записываются как:
Разложение в ряд с помощью функций Бесселя ( ряд Каптейна ) имеет вид
Еще одним важным соотношением для целочисленных порядков является расширение Якоби – Ангера :
В общем, сериал
Отдельные функции допускают специальное представление
В более общем смысле, если f имеет точку ветвления вблизи начала координат такой природы, что
Другой способ определения функций Бесселя — это формула представления Пуассона и формула Мелера-Сонина:
Поскольку уравнение Бесселя становится эрмитовым (самосопряженным), если оно делится на x , решения должны удовлетворять соотношению ортогональности для соответствующих граничных условий. В частности, отсюда следует, что:
Аналогичное соотношение для сферических функций Бесселя следует сразу:
Если определить коробчатую функцию x , которая зависит от малого параметра ε, как:
Тогда замена переменных дает уравнение замыкания : [48]
Другое важное свойство уравнений Бесселя, следующее из тождества Абеля , связано с вронскианом решений:
При α > −1 четная целая функция рода 1 x − а J α ( x ) имеет только вещественные нули. Позволять
(Имеется большое количество других известных интегралов и тождеств, которые здесь не воспроизводятся, но которые можно найти в литературе.)
Рекуррентные отношения [ править ]
Функции J α , Y α , H (1)
α и H (2)
все α удовлетворяют рекуррентным соотношениям [49]
Модифицированные функции Бесселя подчиняются аналогичным соотношениям:
Рекуррентное соотношение читается
Трансцендентность [ править ]
В 1929 году Карл Людвиг Зигель доказал, что J ν ( x ) , J ' ν ( x ) и логарифмическая производная J' ν ( x ) / J ν ( x ) — трансцендентные числа , когда ν рационально, а x алгебраическое и ненулевое. [51] Из того же доказательства также следует, что K ν ( x ) трансцендентно при тех же предположениях. [52]
Теорема умножения [ править ]
Функции Бесселя подчиняются теореме умножения
Нули функции Бесселя [ править ]
Гипотеза Бурже [ править ]
Сам Бессель первоначально доказал, что для неотрицательных целых чисел n уравнение J n ( x ) = 0 имеет бесконечное число решений относительно x . [55] Однако когда функции J n ( x ) изображены на одном и том же графике, ни один из нулей не совпадает для разных значений n, за исключением нуля при x = 0 . Это явление известно как гипотеза Бурже в честь французского математика XIX века, изучавшего функции Бесселя. В частности, он утверждает, что для любых целых чисел n ≥ 0 и m ≥ 1 функции J n ( x ) и J n + m ( x ) не имеют общих нулей, кроме одного в точке x = 0 . Гипотезу доказал Карл Людвиг Зигель в 1929 году. [56]
Трансцендентность [ править ]
Сигел доказал в 1929 году, что когда рационально , все ненулевые корни J ν (x) и J ' ν (x) трансцендентны ν , [57] как и все корни K ν (x) . [52] Также известно, что все корни высших производных при n ≤ 18 трансцендентны, за исключением особых значений и . [57]
Численные подходы [ править ]
Численные исследования нулей функции Бесселя см. в Gil, Segura & Temme (2007) , Kravanja et al. (1998) и Молер (2004) .
Числовые значения [ править ]
Первый ноль в J 0 (т.е. j 0,1 , j 0,2 и j 0,3 ) встречается при аргументах примерно 2,40483, 5,52008 и 8,65373 соответственно. [58]
См. также [ править ]
- Функция гнева
- Полиномы Бесселя
- Функция Бесселя – Клиффорда
- Функция Бесселя – Мейтленда
- Ряд Фурье – Бесселя
- Хана – Экстона Бесселя q -функция
- Преобразование Ханкеля
- Неполные функции Бесселя
- Джексона Бесселя q -функция
- Функции Кельвина
- Kontorovich–Lebedev transform
- Алгоритм Ленца
- Правило сумм Лерша – Ньюбергера
- Функция Ломмеля
- Полином Ломмеля
- Полином Неймана
- Серия Шлёмильха
- Формула Сонина
- Функция Струве
- Колебания круговой мембраны
- Функция Вебера (определенная в функции Гнева )
- Проблема круга Гаусса
Примечания [ править ]
- ^ Виленский, Майкл; Браун, Джордан; Хейзелтон, Брина (июнь 2023 г.). «Почему и когда ожидать распределения гауссовских ошибок в эпоху реионизации измерений спектра мощности на частоте 21 см». Ежемесячные уведомления Королевского астрономического общества . 521 (4): 5191–5206. arXiv : 2211.13576 . дои : 10.1093/mnras/stad863 .
- ^ Вайсштейн, Эрик В. «Сферическая функция Бесселя второго рода» . Математический мир .
- ^ Вайсштейн, Эрик В. «Функция Бесселя второго рода» . Математический мир .
- ↑ Перейти обратно: Перейти обратно: а б Абрамовиц и Стегун, с. 360, 9.1.10 .
- ^ Абрамовиц и Стегун, с. 358, 9.1.5 .
- ↑ Перейти обратно: Перейти обратно: а б Темме, Нико М. (1996). Специальные функции: введение в классические функции математической физики (2-е печатное изд.). Нью-Йорк: Уайли. стр. 228–231. ISBN 0471113131 .
- ^ Вайсштейн, Эрик В. «Формула Хансена-Бесселя» . Математический мир .
- ^ Бессель, Ф. (1824). Соответствующий интеграл представляет собой ненумерованное уравнение между уравнениями 28 и 29. Обратите внимание, что уравнение Бесселя сегодня было бы написано .
- ^ Уотсон, с. 176
- ^ «Свойства функций Ганкеля и Бесселя» . Архивировано из оригинала 23 сентября 2010 г. Проверено 18 октября 2010 г.
- ^ «Интегральные представления функции Бесселя» . www.nbi.dk. Архивировано из оригинала 3 октября 2022 года . Проверено 25 марта 2018 г.
- ^ Арфкен и Вебер, упражнение 11.1.17.
- ^ Абрамовиц и Стегун, с. 362, 9.1.69 .
- ^ Сегё, Габор (1975). Ортогональные полиномы (4-е изд.). Провиденс, Род-Айленд: AMS.
- ^ «Функции Бесселя первого и второго рода» (PDF) . mhtlab.uwaterloo.ca . п. 3. Архивировано (PDF) из оригинала 9 октября 2022 г. Проверено 24 мая 2022 г.
- ^ Цифровая библиотека математических функций NIST , (10.8.1). Доступ онлайн: 25 октября 2016 г.
- ^ Вайсштейн, Эрик В. «Функция Бесселя второго рода» . Математический мир .
- ↑ Перейти обратно: Перейти обратно: а б Ватсон, с. 178 .
- ^ Абрамовиц и Стегун, с. 358, 9.1.3, 9.1.4 .
- ^ Абрамовиц и Стегун, с. 358, 9.1.6 .
- ^ Абрамовиц и Стегун, с. 360, 9.1.25 .
- ^ Абрамовиц и Стегун, с. 375, 9.6.2, 9.6.10, 9.6.11 .
- ^ Диксон; Феррар, WL (1930). «Прямое доказательство интеграла Николсона». Ежеквартальный математический журнал . Оксфорд: 236–238. дои : 10.1093/qmath/os-1.1.236 .
- ^ Абрамовиц и Стегун, с. 375, 9.6.3, 9.6.5 .
- ^ Абрамовиц и Стегун, с. 374, 9.6.1 .
- ^ Грейнер, Уолтер; Рейнхардт, Иоахим (2009). Квантовая электродинамика . Спрингер. п. 72. ИСБН 978-3-540-87561-1 .
- ^ Уотсон, с. 181 .
- ^ Хоконов, М.Х. (2004). «Каскадные процессы потери энергии за счет испускания жестких фотонов». Журнал экспериментальной и теоретической физики . 99 (4): 690–707. Бибкод : 2004JETP...99..690K . дои : 10.1134/1.1826160 . S2CID 122599440 . . Получено по формулам И. С. Градштейна и И. М. Рыжика , Таблица интегралов, рядов и произведений (Физматгиз, Москва, 1963; Academic Press, Нью-Йорк, 1980).
- ^ Упоминается как таковой в: Тейхроу, Д. (1957). «Смесь нормальных распределений с различными дисперсиями» (PDF) . Анналы математической статистики . 28 (2): 510–512. дои : 10.1214/aoms/1177706981 .
- ^ Абрамовиц и Стегун, с. 437, 10.1.1 .
- ^ Абрамовиц и Стегун, с. 439, 10.1.25, 10.1.26 .
- ^ Абрамовиц и Стегун, с. 438, 10.1.11 .
- ^ Абрамовиц и Стегун, с. 438, 10.1.12 .
- ^ Абрамовиц и Стегун, с. 439, 10.1.39 .
- ^ Л. В. Бабушкина, М. К. Керимов, А. И. Никитин, Алгоритмы вычисления функций Бесселя полуцелого порядка с комплексными аргументами, с. 110, с. 111 .
- ^ Абрамовиц и Стегун, с. 439, 10.1.23, 10.1.24 .
- ^ Гриффитс. Введение в квантовую механику, 2-е издание, с. 154.
- ^ Ду, Хонг (2004). «Расчет Ми-рассеяния». Прикладная оптика . 43 (9): 1951–1956. Бибкод : 2004ApOpt..43.1951D . дои : 10.1364/ao.43.001951 . ПМИД 15065726 .
- ^ Абрамовиц и Стегун, с. 364, 9.2.1 .
- ^ NIST Цифровая библиотека математических функций , раздел 10.11 .
- ^ Абрамовиц и Стегун, с. 377, 9.7.1 .
- ^ Абрамовиц и Стегун, с. 378, 9.7.2 .
- ^ Фрелих и Спенсер, 1981, Приложение B.
- ^ Сун, С.; Ховден, Р. (2022). «О бесконечных рядах функций Бесселя первого рода». arXiv : 2211.01148 [ math-ph ].
- ^ Абрамовиц и Стегун, с. 363, 9.1.82 и далее.
- ^ Уотсон, Дж.Н. (25 августа 1995 г.). Трактат по теории функций Бесселя . Издательство Кембриджского университета. ISBN 9780521483919 . Проверено 25 марта 2018 г. - через Google Книги.
- ^ Градштейн Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Героним Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015) [октябрь 2014 г.]. «8.411.10.». В Цвиллингере, Дэниел; Молл, Виктор Гюго (ред.). Таблица интегралов, рядов и произведений . Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. ISBN 978-0-12-384933-5 . LCCN 2014010276 .
- ^ Арфкен и Вебер, раздел 11.2.
- ^ Абрамовиц и Стегун, с. 361, 9.1.27 .
- ^ Абрамовиц и Стегун, с. 361, 9.1.30 .
- ^ Сигел, Карл Л. (2014). «О некоторых приложениях диофантовых приближений» . О некоторых применениях диофантовых приближений: перевод книги Карла Людвига Зигеля «О некоторых применениях диофантовых приближений» Клеменса Фукса с комментарием и статьей «Целочисленные точки на кривых: теорема Зигеля после доказательства Зигеля Клеменса Фукса и Умберто Заньера» (на немецком языке). Высшая нормальная школа. стр. 81–138. дои : 10.1007/978-88-7642-520-2_2 . ISBN 978-88-7642-520-2 .
- ↑ Перейти обратно: Перейти обратно: а б Джеймс, РД (ноябрь 1950 г.). «Обзор: Карл Людвиг Зигель, Трансцендентные числа» . Бюллетень Американского математического общества . 56 (6): 523–526. дои : 10.1090/S0002-9904-1950-09435-X .
- ↑ Перейти обратно: Перейти обратно: а б Абрамовиц и Стегун, с. 363, 9.1.74 .
- ^ Трусделл, К. (1950). «О теоремах сложения и умножения специальных функций» . Труды Национальной академии наук . 1950 (12): 752–757. Бибкод : 1950ПНАС...36..752Т . дои : 10.1073/pnas.36.12.752 . ПМЦ 1063284 . ПМИД 16578355 .
- ^ Бессель, Ф. (1824), статья 14.
- ^ Уотсон, стр. 484–485.
- ↑ Перейти обратно: Перейти обратно: а б Лорх, Ли; Малдун, Мартин Э. (1995). «Трансцендентность нулей высших производных функций, включающих функции Бесселя» . Международный журнал математики и математических наук . 18 (3): 551–560. дои : 10.1155/S0161171295000706 .
- ^ Абрамовиц и Стегун, стр. 409.
Ссылки [ править ]
- Абрамовиц, Милтон ; Стегун, Ирен Энн , ред. (1983) [июнь 1964 г.]. «Глава 9» . Справочник по математическим функциям с формулами, графиками и математическими таблицами . Серия «Прикладная математика». Том. 55 (Девятое переиздание с дополнительными исправлениями десятого оригинального издания с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон, округ Колумбия; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Дуврские публикации. стр. 355, 435. ISBN. 978-0-486-61272-0 . LCCN 64-60036 . МР 0167642 . LCCN 65-12253 . См. также главу 10 .
- Арфкен, Джордж Б. и Ханс Дж. Вебер, Математические методы для физиков , 6-е издание (Harcourt: Сан-Диего, 2005). ISBN 0-12-059876-0 .
- Бессель, Фридрих (1824). «Исследование той части планетарных возмущений, которые возникают из-за движения Солнца». Берлинские трактаты . Воспроизведено на страницах 84–109 в Трактаты Фридриха Вильгельма Бесселя . Лейпциг: Энгельманн. 1875. Английский перевод текста .
- Боуман, Франк «Введение в функции Бесселя» (Дувр: Нью-Йорк, 1958). ISBN 0-486-60462-4 .
- Гил, А.; Сегура, Дж.; Темме, Нью-Мексико (2007). Численные методы для специальных функций . Общество промышленной и прикладной математики.
- Краванья, П. ; Рагос, О.; Врахатис, Миннесота; Зафиропулос, Ф.А. (1998), «ZEBEC: Пакет математического программного обеспечения для вычисления простых нулей функций Бесселя вещественного порядка и комплексного аргумента», Computer Physics Communications , 113 (2–3): 220–238, Бибкод : 1998CoPhC.113. .220K , doi : 10.1016/S0010-4655(98)00064-2
- Ми, Г. (1908). «Вклад в оптику мутных сред, особенно коллоидных растворов металлов» . Анналы физики . 25 (3): 377. Бибкод : 1908АнП...330..377М . дои : 10.1002/andp.19083300302 .
- Олвер, ФВДж ; Максимон, LC (2010), «Функция Бесселя» , в Олвере, Фрэнке В.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN 978-0-521-19225-5 , МР 2723248 ..
- Пресс, WH ; Теукольский, С.А.; Феттерлинг, WT; Фланнери, Б.П. (2007), «Раздел 6.5. Функции Бесселя целочисленного порядка» , Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8 , заархивировано из оригинала 03 февраля 2021 г. , получено 28 сентября 2022 г.
- B Испания, М.Г. Смит, Функции математической физики , Van Nostand Reinhold Company, Лондон, 1970. Глава 9 посвящена функциям Бесселя.
- Н. М. Темме, Специальные функции. Введение в классические функции математической физики , John Wiley and Sons, Inc., Нью-Йорк, 1996. ISBN 0-471-11313-1 . Глава 9 посвящена функциям Бесселя.
- Уотсон, Дж. Н. , Трактат по теории функций Бесселя, второе издание , (1995) Издательство Кембриджского университета. ISBN 0-521-48391-3 .
- Вебер, Генрих (1873), «О представлении произвольных функций функциями Бесселя», Mathematical Annals , 6 (2): 146–161, doi : 10.1007/BF01443190 , S2CID 122409461 .
Внешние ссылки [ править ]
- Лизоркин, П.И. (2001) [1994], «Функции Бесселя» , Энциклопедия Математики , EMS Press .
- Кармазина Л.Н.; Прудников, А.П. (2001) [1994], «Цилиндровая функция» , Энциклопедия Математики , EMS Press .
- Розов, Н.Х. (2001) [1994], «Уравнение Бесселя» , Математическая энциклопедия , EMS Press .
- Страницы функций Wolfram с функциями Бесселя J и Y , а также модифицированными Бесселя I и K. функциями Страницы содержат формулы, средства оценки функций и калькуляторы для построения графиков.
- Вайсштейн, Эрик В. «Функции Бесселя первого рода» . Математический мир .
- Функции Бесселя J ν , Y ν , I ν и K ν Librow в справочнике Function .
- Ф.В.Дж. Олвер, Л.К. Максимон, Функции Бесселя (глава 10 Цифровой библиотеки математических функций).
- Молер, CB (2004). Численные вычисления с MATLAB (PDF) . Общество промышленной и прикладной математики. Архивировано из оригинала (PDF) 8 августа 2017 г.


















![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&=J_{\alpha }(x)+iY_{\alpha }(x),\\[5pt]H_{ \alpha }^{(2)}(x)&=J_{\alpha }(x)-iY_{\alpha }(x),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa434f6bcee175b4ff90fde5ba2fb596a41b90c3)






![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_ {\alpha }(x)}{i\sin \alpha \pi }},\\[5pt]H_{\alpha }^{(2)}(x)&={\frac {J_{-\alpha } (x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin \alpha \pi }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2748efe7f4138a71b2bf84ed77bc90d4bf0810)
![{\displaystyle {\begin{aligned}H_{-\alpha }^{(1)}(x)&=e^{\alpha \pi i}H_{\alpha }^{(1)}(x), \\[6mu]H_{-\alpha }^{(2)}(x)&=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x).\end{ выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99f0226c9673919c5c9a95041395384711081474)
![{\displaystyle {\begin{aligned}J_{-(m+{\frac {1}{2}})}(x)&=(-1)^{m+1}Y_{m+{\frac {1} {2}}}(x),\\[5pt]Y_{-(m+{\frac {1}{2}})}(x)&=(-1)^{m}J_{m+{\frac {1}{2}}}(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9f3ac2da371d4ddcb7b0694f5e7fca8c7453803)
![{\displaystyle {\begin{aligned}H_{\alpha }^{(1)}(x)&={\frac {1}{\pi i}}\int _{-\infty }^{+\infty +\pi i}e^{x\sinh t-\alpha t}\,dt,\\[5pt]H_{\alpha }^{(2)}(x)&=-{\frac {1} \pi i}}\int _{-\infty }^{+\infty -\pi i}e^{x\sinh t-\alpha t}\,dt,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28973dd4cdae45d03d4ed47926313658638682d6)
![{\displaystyle {\begin{aligned}I_{\alpha }(x)&=i^{-\alpha }J_{\alpha }(ix)=\sum _{m=0}^{\infty }{\ frac {1}{m!\,\Gamma (m+\alpha +1)}}\left({\frac {x}{2}}\right)^{2m+\alpha },\\[5pt]K_{ \alpha }(x)&={\frac {\pi }{2}}{\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin \alpha \pi } },\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a0b68640cfbec56a6b6ad53c432371549dcfedd)






![{\displaystyle {\begin{aligned}J_{\alpha }(iz)&=e^{\frac {\alpha \pi i}{2}}I_{\alpha }(z),\\[1ex]Y_ {\alpha }(iz)&=e^{\frac {(\alpha +1)\pi i}{2}}I_{\alpha }(z)-{\tfrac {2}{\pi }}e ^{-{\frac {\alpha \pi i}{2}}}K_{\alpha }(z).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4460424d9d6b98161589dd4aa46ad6429678c189)

![{\displaystyle {\begin{aligned}I_{\alpha }(x)&={\frac {1}{\pi }}\int _{0}^{\pi }e^{x\cos \theta } \cos \alpha \theta \,d\theta -{\frac {\sin \alpha \pi }{\pi }}\int _{0}^{\infty }e^{-x\cosh t-\alpha t}\,dt,\\[5pt]K_{\alpha }(x)&=\int _{0}^{\infty }e^{-x\cosh t}\cosh \alpha t\,dt. \end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c907de8d37caf8e5e482ce5005e8941ab401bd4b)

![{\displaystyle {\begin{aligned}K_{\frac {1}{3}}(\xi )&={\sqrt {3}}\int _{0}^{\infty }\exp \left(- \xi \left(1+{\frac {4x^{2}}{3}}\right){\sqrt {1+{\frac {x^{2}}{3}}}}\right)\ ,dx,\\[5pt]K_{\frac {2}{3}}(\xi )&={\frac {1}{\sqrt {3}}}\int _{0}^{\infty } {\frac {3+2x^{2}}{\sqrt {1+{\frac {x^{2}}{3}}}}}\exp \left(-\xi \left(1+{\ frac {4x^{2}}{3}}\right){\sqrt {1+{\frac {x^{2}}{3}}}}\right)\,dx.\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/526dd0ae355e44f4bd2608b20d39d07da0fff979)








![{\displaystyle {\begin{alignedat}{2}j_{n}(x)&={\frac {\pi }{2x}}J_{n+{\frac {1}{2}}}(x)= \\&={\frac {1}{2x}}\left[e^{ix}\sum _{r=0}^{n}{\frac {i^{rn-1}(n+r) !}{r!(nr)!(2x)^{r}}}+e^{-ix}\sum _{r=0}^{n}{\frac {(-i)^{rn-1 }(n+r)!}{r!(nr)!(2x)^{r}}}\right]\\&={\frac {1}{x}}\left[\sin \left(x -{\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{\frac {n}{2}}\right]}{\frac {(-1 )^{r}(n+2r)!}{(2r)!(n-2r)!(2x)^{2r}}}+\cos \left(x-{\frac {n\pi }{2 }}\right)\sum _{r=0}^{\left[{\frac {n-1}{2}}\right]}{\frac {(-1)^{r}(n+2r +1)!}{(2r+1)!(n-2r-1)!(2x)^{2r+1}}}\right]\\y_{n}(x)&=(-1)^ {n+1}j_{-n-1}(x)=(-1)^{n+1}{\frac {\pi }{2x}}J_{-\left(n+{\frac {1} {2}}\right)}(x)=\\&={\frac {(-1)^{n+1}}{2x}}\left[e^{ix}\sum _{r=0 }^{n}{\frac {i^{r+n}(n+r)!}{r!(nr)!(2x)^{r}}}+e^{-ix}\sum _{ r=0}^{n}{\frac {(-i)^{r+n}(n+r)!}{r!(nr)!(2x)^{r}}}\right]=\ \&={\frac {(-1)^{n+1}}{x}}\left[\cos \left(x- {\frac {n\pi }{2}}\right)\sum _ {r=0}^{\left[{\frac {n}{2}}\right]}{\frac {(-1)^{r}(n+2r)!}{(2r)!(n -2r)!(2x)^{2r}}}+\sin \left(x- {\frac {n\pi }{2}}\right)\sum _{r=0}^{\left[{ \frac {n-1}{2}}\right]}{\frac {(-1)^{r}(n+2r+1)!}{(2r+1)!(n-2r-1) !(2x)^{2r+1}}}\right]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bb3372a5d9d734b5aa2e867e7d28a7a2b825cd2)








![{\displaystyle Y_{\alpha }(z)\sim {\begin{cases}{\dfrac {2}{\pi }}\left(\ln \left({\dfrac {z}{2}}\right )+\gamma \right)&{\text{if }}\alpha =0\\[1ex]-{\dfrac {\Gamma (\alpha )}{\pi }}\left({\dfrac {2} {z}}\right)^{\alpha }+{\dfrac {1}{\Gamma (\alpha +1)}}\left({\dfrac {z}{2}}\right)^{\alpha }\cot(\alpha \pi )&{\text{if }}\alpha {\text{ — положительное целое число (один член доминирует, если }}\alpha {\text{ не является мнимым)}},\\[1ex ]-{\dfrac {(-1)^{\alpha }\Gamma (-\alpha )}{\pi }}\left({\dfrac {z}{2}}\right)^{\alpha }& {\text{if }}\alpha {\text{ — отрицательное целое число,}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0478d18ffc1f12108ee81de9db5e1f89f322db6)


![{\displaystyle {\begin{aligned}J_{\alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z}}}e^{i\left(z- {\frac { \alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text{for }}-\pi <\arg z<0,\\[1ex]J_{ \alpha }(z)&\sim {\frac {1}{\sqrt {2\pi z}}}e^{-i\left(z- {\frac {\alpha \pi }{2}}- {\frac {\pi }{4}}\right)}&&{\text{for }}0<\arg z<\pi ,\\[1ex]Y_{\alpha }(z)&\sim -i {\frac {1}{\sqrt {2\pi z}}}e^{i\left(z- {\frac {\alpha \pi }{2}}-{\frac {\pi }{4} }\right)}&&{\text{for }}-\pi <\arg z<0,\\[1ex]Y_{\alpha }(z)&\sim i{\frac {1}{\sqrt { 2\pi z}}}e^{-i\left(z- {\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}&&{\text {for }}0<\arg z<\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c892df890c00f5a4bc2d13ae3b02ea0abb79aec1)


![{\displaystyle {\begin{aligned}I_{\alpha }(z)={\frac {1}{{\sqrt {2\pi z}}{\sqrt[{4}]{1+{\frac { \alpha ^{2}}{z^{2}}}}}}}\exp \left(-\alpha \operatorname {arsinh} \left({\frac {\alpha }{z}}\right)+ z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}\right)\left(1+{\mathcal {O}}\left({\frac { 1}{z{\sqrt {1+{\frac {\alpha ^{2}}{z^{2}}}}}}}\right)\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f57e4803db262b5efdc20c32da3835c3fd4f0f9d)
![{\displaystyle {\begin{aligned}I_{{1}/{2}}(z)&={\sqrt {\frac {2}{\pi }}}{\frac {\sinh(z)}{ \sqrt {z}}}\sim {\frac {e^{z}}{\sqrt {2\pi z}}}&&{\text{for }}\left|\arg z\right|<{\ tfrac {\pi }{2}},\\[1ex]K_{{1}/{2}}(z)&={\sqrt {\frac {\pi }{2}}}{\frac {e ^{-z}}{\sqrt {z}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec3a7941e679aaacaf61d90117613ee90a23851)

![{\displaystyle {\begin{aligned}I_{\alpha }(z)&\sim {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {z}{2}} \right)^{\alpha },\\[1ex]K_{\alpha }(z)&\sim {\begin{cases}-\ln \left({\dfrac {z}{2}}\right) -\gamma &{\text{if }}\alpha =0\\[1ex]{\frac {\Gamma (\alpha )}{2}}\left({\dfrac {2}{z}}\right )^{\alpha }&{\text{if }}\alpha >0\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfbbf3eae419f2a44adfb496e7ccb657439bdaf7)



![{\textstyle \sum _{\nu =-\infty }^{\infty }J_{3\nu +p}(x)={\frac {1}{3}}\left[1+2\cos { (x{\sqrt {3}}/2-2\pi p/3)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eaa4c63e9da373d3678e16136bd9a11688985bd)














![{\displaystyle {\begin{aligned}J_{\nu }(z)&={\frac {\left({\frac {z}{2}}\right)^{\nu }}{\Gamma \left (\nu +{\frac {1}{2}}\right){\sqrt {\pi }}}}\int _{-1}^{1}e^{izs}\left(1-s^ {2}\right)^{\nu -{\frac {1}{2}}}\,ds\\[5px]&={\frac {2}{{\left({\frac {z}{ 2}}\right)}^{\nu }\cdot {\sqrt {\pi }}\cdot \Gamma \left({\frac {1}{2}}-\nu \right)}}\int _ {1}^{\infty }{\frac {\sin zu}{\left(u^{2}-1\right)^{\nu +{\frac {1}{2}}}}}\, du\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248363b3af99701e32dcec48127f0dfc6e7586bf)
![{\displaystyle \int _{0}^{1}xJ_{\alpha }\left(xu_{\alpha,m}\right)J_{\alpha }\left(xu_{\alpha,n}\right)\ ,dx={\frac {\delta _{m,n}}{2}}\left[J_{\alpha +1}\left(u_{\alpha,m}\right)\right]^{2} = {\frac {\delta _{m,n}}{2}}\left[J_{\alpha }'\left(u_{\alpha,m}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4901ce8ec95f647c69297f8a6a92d245466ba632)
![{\displaystyle \int _{0}^{1}x^{2}j_{\alpha }\left(xu_{\alpha,m}\right)j_{\alpha }\left(xu_{\alpha,n }\right)\,dx={\frac {\delta _{m,n}}{2}}\left[j_{\alpha +1}\left(u_{\alpha ,m}\right)\right ]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de6fbc1b8ac85fb7dd6253a931d1b78cec9b89ae)












![{\displaystyle {\begin{aligned}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{m}\left[x^{\alpha }Z_{ \alpha }(x)\right]&=x^{\alpha -m}Z_{\alpha -m}(x),\\\left({\frac {1}{x}}{\frac {d }{dx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]&=(-1)^{m} {\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}.\end{alpha +m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c59565e99a36cfef8426d543521d8e4df7bc07a2)



![{\displaystyle {\begin{aligned}C_{\alpha -1}(x)-C_{\alpha +1}(x)&={\frac {2\alpha }{x}}C_{\alpha }( x),\\[1ex]C_{\alpha -1}(x)+C_{\alpha +1}(x)&=2{\frac {d}{dx}}C_{\alpha }(x) ,\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8390e0da90e49d8017a003ce6e00d8a2358dc06)







