сверхрешетка

Сверхрешетка — это периодическая структура из слоев двух (или более) материалов. Обычно толщина одного слоя составляет несколько нанометров . Это также может относиться к структуре более низкой размерности, такой как массив квантовых точек или квантовых ям .

Открытие

Сверхрешетки были открыты в начале 1925 года Йоханссоном и Линде. после изучения систем золото - медь и палладий -медь с помощью их особых рентгенограмм. Дальнейшие экспериментальные наблюдения и теоретические модификации в этой области были проведены Брэдли и Джеем. Горский, Борелиус, Делингер и Граф, Брэгг и Уильямс и Бете. Теории основывались на переходе расположения атомов в кристаллических решетках из неупорядоченного состояния в упорядоченное .

Механические свойства

Дж. С. Келер теоретически предсказал что при использовании чередующихся (нано) слоев материалов с высокими и низкими упругими постоянными сопротивление сдвигу увеличивается до 100 раз, поскольку -Рида Франка источник дислокаций не может работать в нанослоях.

Повышенная механическая твердость таких сверхрешетчатых материалов была впервые подтверждена Лехоцким в 1978 году на Al-Cu и Al-Ag. а затем несколькими другими, такими как Барнетт и Спроул. на твердых PVD- покрытиях.

Полупроводниковые свойства

Если сверхрешетка состоит из двух полупроводниковых материалов с разными запрещенными зонами , каждая квантовая яма устанавливает новые правила отбора , которые влияют на условия прохождения зарядов через структуру. Два разных полупроводниковых материала поочередно наносятся друг на друга, образуя периодическую структуру в направлении роста. С момента предложения Эсаки и Цу в 1970 году синтетических сверхрешеток , были достигнуты успехи в физике таких сверхтонких полупроводников, которые сейчас называются квантовыми структурами. Концепция квантового ограничения привела к наблюдению квантово-размерных эффектов в изолированных гетероструктурах с квантовыми ямами и тесно связана со сверхрешетками через явления туннелирования. Поэтому эти две идеи часто обсуждаются на одной и той же физической основе, но каждая из них имеет разную физику, полезную для приложений в электрических и оптических устройствах.

Типы полупроводниковых сверхрешеток

Минизонные сверхрешеточные структуры зависят от типа гетероструктуры : типа I , типа II или типа III . Для типа I дно зоны проводимости и верх валентной подзоны образуются в одном полупроводниковом слое. При типе II подзоны проводимости и валентные зоны расположены в шахматном порядке как в реальном, так и в обратном пространстве , так что электроны и дырки удерживаются в разных слоях. Сверхрешетки типа III включают полуметаллический материал, такой как HgTe/ CdTe . Хотя дно подзоны проводимости и верх валентной подзоны формируются в одном и том же полупроводниковом слое в сверхрешетке типа III, которая аналогична сверхрешетке типа I, ширина запрещенной зоны сверхрешеток типа III может плавно регулироваться от полупроводниковой до нулевой зоны. материал запрещенной зоны и полуметалл с отрицательной запрещенной зоной.

Другой класс квазипериодических сверхрешеток назван в честь Фибоначчи . Сверхрешетку Фибоначчи можно рассматривать как одномерный квазикристалл , в котором либо прыжковый перенос электрона, либо энергия на месте принимают два значения, расположенные в последовательности Фибоначчи .

Полупроводниковые материалы

Сверхрешетка GaAs/AlAs и потенциальный профиль зон проводимости и валентной зоны вдоль направления роста (z).

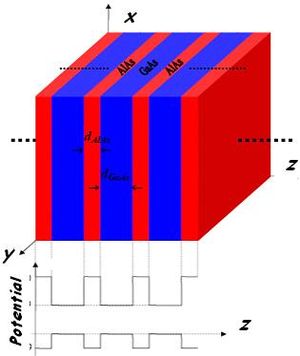
Полупроводниковые материалы, которые используются для изготовления сверхрешеточных структур, можно разделить по группам элементов: IV, III-V и II-VI. В то время как полупроводники групп III-V (особенно GaAs/Al _x Ga _1-x As) широко изучены, гетероструктуры группы IV, такие как система Si _x Ge _1-x, реализовать гораздо труднее из-за большого несоответствия решеток. Тем не менее деформационная модификация подзонных структур в этих квантовых структурах интересна и привлекает большое внимание.

В системе GaAs/AlAs как разница в постоянной решетки между GaAs и AlAs, так и разница в их коэффициентах теплового расширения невелики. Таким образом, остаточная деформация при комнатной температуре может быть минимизирована после охлаждения от температур эпитаксиального роста . Первая композиционная сверхрешетка была реализована с использованием системы материалов GaAs/Al _x Ga _1−x As.

Система графен / нитрид бора образует полупроводниковую сверхрешетку, когда два кристалла выровнены. Его носители заряда движутся перпендикулярно электрическому полю с небольшой диссипацией энергии. h-BN имеет гексагональную структуру, похожую на структуру графена. Сверхрешетка нарушила инверсионную симметрию . Локально топологические токи сравнимы по силе с приложенным током, что указывает на большие углы долины-Холла.

Производство

Сверхрешетки можно производить различными методами, но наиболее распространенными являются молекулярно-лучевая эпитаксия (МЛЭ) и распыление . С помощью этих методов можно создавать слои толщиной всего в несколько атомных расстояний. Пример задания сверхрешетки: [ Fe
₂₀ В
₃₀ ] ₂₀ . Он описывает двойной слой из 20 Å железа (Fe) и 30 Å ванадия (V), повторяющийся 20 раз, что дает общую толщину 1000 Å или 100 нм. Технология МЛЭ как средство изготовления полупроводниковых сверхрешеток имеет первостепенное значение. В дополнение к технологии MBE, металлоорганическое химическое осаждение из газовой фазы (MO-CVD) способствовало разработке сверхпроводниковых сверхрешеток, которые состоят из полупроводников четвертичных соединений III-V, таких как сплавы InGaAsP. Новые методы включают комбинацию обработки источника газа с технологиями сверхвысокого вакуума (СВВ), такими как металлорганические молекулы в качестве исходных материалов и MBE-источник газа с использованием гибридных газов, таких как арсин ( AsH
₃ ) и фосфин ( PH
₃ ) были разработаны.

Вообще говоря, МЛЭ представляет собой метод использования трех температур в бинарных системах, например, температуры подложки, температуры исходного материала элементов группы III и группы V в случае соединений III-V.

Структурное качество полученных сверхрешеток можно проверить с помощью спектров рентгеновской дифракции или нейтронной дифракции , которые содержат характерные сателлитные пики. Другими эффектами, связанными с чередующимся расслоением, являются: гигантское магнитосопротивление , настраиваемая отражательная способность рентгеновских и нейтронных зеркал, спиновая поляризация нейтронов и изменения упругих и акустических свойств. В зависимости от природы компонентов сверхрешетку можно назвать магнитной , оптической или полупроводниковой .

Рассеяние рентгеновских лучей и нейтронов на сверхрешетке [Fe ₂₀ V ₃₀ ] ₂₀ .

Структура мини-зоны

Схематическая структура периодической сверхрешетки показана ниже, где A и B — два полупроводниковых материала с соответствующей толщиной слоя a и b (период: $d=a+b$). Когда a и b не слишком малы по сравнению с межатомным расстоянием, адекватное приближение получается путем замены этих быстро меняющихся потенциалов эффективным потенциалом, полученным из зонной структуры исходных объемных полупроводников. Нетрудно решить одномерные уравнения Шредингера в каждом из отдельных слоев, решения которых $\psi$ представляют собой линейные комбинации действительных или мнимых экспонент.

При большой толщине барьера туннелирование является слабым возмущением по отношению к несвязанным бездисперсионным состояниям, которые также полностью ограничены. В этом случае дисперсионное соотношение $E_{z}(k_{z})$, периодическое течение $2\pi /d$ с более чем $d=a+b$ в силу теоремы Блоха полностью синусоидальна:

$\ E_{z}(k_{z})={\frac {\Delta }{2}}(1-\cos(k_{z}d))$

и эффективная масса меняет знак для $2\pi /d$:

$\ {m^{*}={\frac {\hbar ^{2}}{\partial ^{2}E/\partial k^{2}}}}|_{k=0}$

В случае мини-зон этот синусоидальный характер уже не сохраняется. Только высоко в мини-диапазоне (для волновых векторов, значительно превышающих $2\pi /d$) является вершиной, которая фактически «ощущается» и имеет знак изменения эффективной массы. Форма дисперсии мини-зон сильно влияет на транспорт мини-зон, и для широких мини-зон необходимы точные расчеты дисперсионных соотношений. Условием наблюдения одиночного минизонного транспорта является отсутствие межминизонного переноса каким-либо процессом. Тепловой квант k _B T должен быть много меньше разности энергий $E_{2}-E_{1}$ между первой и второй мини-зонами даже при наличии приложенного электрического поля.

Блох утверждает

Для идеальной сверхрешетки полный набор состояний собственных состояний может быть построен как произведение плоских волн. $e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi$ и z -зависимая функция $f_{k}(z)$ которое удовлетворяет уравнению собственных значений

$\left(E_{c}(z)-{\frac {\partial }{\partial z}}{\frac {\hbar ^{2}}{2m_{c}(z)}}{\frac {\partial }{\partial z}}+{\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\right)f_{k}(z)=Ef_{k}(z)$.

Как $E_{c}(z)$ и $m_{c}(z)$ — периодические функции с периодом сверхрешетки d , собственные состояния — состояние Блоха. $f_{k}(z)=\phi _{q,\mathbf {k} }(z)$ с энергией $E^{\nu }(q,\mathbf {k} )$. первого порядка В рамках теории возмущений по k ² , получим энергию

$E^{\nu }(q,\mathbf {k} )\approx E^{\nu }(q,\mathbf {0} )+\langle \phi _{q,\mathbf {k} }\mid {\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\mid \phi _{q,\mathbf {k} }\rangle$.

Сейчас, $\phi _{q,\mathbf {0} }(z)$ будет демонстрировать большую вероятность в яме, так что кажется разумным заменить второй член на

$E_{k}={\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{w}}}$

где $m_{w}$ — эффективная масса квантовой ямы.

Функции Ванье

По определению функции Блоха делокализованы по всей сверхрешетке. Это может создать трудности, если применяются электрические поля или учитываются эффекты, связанные с конечной длиной сверхрешетки. Поэтому часто бывает полезно использовать разные наборы базисных состояний, которые лучше локализованы. Заманчивым выбором было бы использование собственных состояний одиночных квантовых ям. Тем не менее, у такого выбора есть серьезный недостаток: соответствующие состояния являются решениями двух разных гамильтонианов , каждое из которых игнорирует наличие другой ямы. Таким образом, эти состояния не ортогональны, что создает сложности. Обычно в рамках этого подхода связь оценивается с помощью гамильтониана переноса. По этим причинам удобнее использовать набор функций Ванье .

Лестница Ванье-Старка

Приложение электрического поля F к сверхрешеточной структуре приводит к тому, что гамильтониан проявляет дополнительный скалярный потенциал eφ ( z ) = − eFz , который разрушает трансляционную инвариантность. В этом случае, учитывая собственное состояние с волновой функцией $\Phi _{0}(z)$ и энергия $E_{0}$, то набор состояний, соответствующих волновым функциям $\Phi _{j}(z)=\Phi _{0}(z-jd)$ являются собственными состояниями гамильтониана с энергиями E _j = E ₀ − jeFd . Эти состояния одинаково разнесены как в энергетическом, так и в реальном пространстве и образуют так называемую лестницу Ванье-Старка . Потенциал $\Phi _{0}(z)$ не ограничен для бесконечного кристалла, что предполагает непрерывный энергетический спектр. Тем не менее характерный энергетический спектр этих лестниц Ванье – Штарка можно было разрешить экспериментально.

Транспорт

Обзор различных стандартных подходов к транспортировке сверхрешеток.

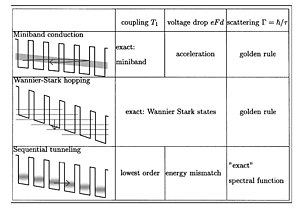
Движение носителей заряда в сверхрешетке отличается от движения в отдельных слоях: может быть повышена подвижность носителей заряда, что выгодно для высокочастотных устройств, а специфические оптические свойства используются в полупроводниковых лазерах .

Если к проводнику, например металлу или полупроводнику, приложено внешнее смещение, обычно генерируется электрический ток. Величина этого тока определяется зонной структурой материала, процессами рассеяния, напряженностью приложенного поля и равновесным распределением носителей тока в проводнике.

Частный случай сверхрешеток, называемый суперполосками, состоит из сверхпроводящих блоков, разделенных прокладками. В каждой минизоне сверхпроводящий параметр порядка, называемый сверхпроводящей щелью, принимает разные значения, создавая многозонную, двухзонную или многозонную сверхпроводимость.

Недавно Феликс и Перейра исследовали тепловой перенос фононами в периодических и квазипериодический сверхрешетки графен-hBN согласно последовательности Фибоначчи. Они сообщили, что вклад когерентного теплового транспорта (фононного типа волны) подавляется по мере увеличения квазипериодичности.

Другие размеры

Вскоре после того, как двумерные электронные газы ( 2DEG ) стали широко доступны для экспериментов, исследовательские группы попытались создать структуры. это можно было бы назвать 2D искусственными кристаллами. Идея состоит в том, чтобы подвергнуть электроны, находящиеся на границе раздела между двумя полупроводниками (т.е. вдоль направления z ), дополнительному потенциалу модуляции V ( x , y ). В отличие от классических сверхрешеток (1D/3D, то есть одномерной модуляции электронов в трехмерном объеме), описанных выше, это обычно достигается путем обработки поверхности гетероструктуры: нанесения металлического затвора с соответствующим рисунком или травления. Если амплитуда V ( x , y ) велика (возьмем $V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0$ в качестве примера) по сравнению с уровнем Ферми, $|V_{0}|\gg E_{f}$, электроны в сверхрешетке должны вести себя аналогично электронам в атомном кристалле с квадратной решеткой (в примере эти «атомы» будут расположены в позициях ( na , ma ), где n , m — целые числа).

Разница заключается в масштабах длины и энергии. Константы решетки атомных кристаллов имеют порядок 1 Å, тогда как константы сверхрешеток ( а ) на несколько сотен или тысяч больше, что диктуется технологическими ограничениями (например, электронно-лучевая литография, используемая для формирования рисунка на поверхности гетероструктуры). В сверхрешетках соответственно меньше энергии. Использование простой квантовомеханической модели ограниченных частиц предполагает $E\propto 1/a^{2}$. Это соотношение является лишь приблизительным руководством и фактическими расчетами с актуальными в настоящее время графеном (природным атомным кристаллом) и искусственным графеном. (сверхрешетка) показывают, что характерные ширины зон составляют порядка 1 эВ и 10 мэВ соответственно. В режиме слабой модуляции ( $|V_{0}|\ll E_{f}$), происходят такие явления, как колебания соизмеримости или фрактальные энергетические спектры ( «бабочка Хофштадтера» ).

Искусственные двумерные кристаллы можно рассматривать как вариант 2D/2D (2D-модуляция 2D-системы), и экспериментально доступны другие комбинации: массив квантовых проводов (1D/2D) или фотонные кристаллы 3D/3D .

Приложения

Сверхрешетка системы палладий-медь используется в высокоэффективных сплавах для обеспечения более высокой электропроводности, чему способствует упорядоченная структура. Дополнительные легирующие элементы, такие как серебро , рений , родий и рутений, добавляются для лучшей механической прочности и высокотемпературной стабильности. Этот сплав используется для изготовления игл датчиков в картах датчиков .

См. также

• Упорядочение типа Cu-Pt в полупроводниках III-V
• Трубчатые наноструктуры
• Функция Ванье

Ссылки

• Х. Т. Гран, «Полупроводниковые сверхрешетки» , World Scientific (1995). ISBN   978-981-02-2061-7
• Шуллер, И. (1980). «Новый класс слоистых материалов». Письма о физических отзывах . 44 (24): 1597–1600. Бибкод : 1980PhRvL..44.1597S . doi : 10.1103/PhysRevLett.44.1597 .
• Мортен Ягд Кристенсен, «Эпитаксия, тонкие пленки и сверхрешетки» , Национальная лаборатория Рисё, (1997). ISBN   8755022987 Суперрешетка в Google Книгах [1]
• К. Хамагучи, «Основы физики полупроводников» , Springer (2001). Сверхрешетка в Google Книгах ISBN   3540416390
• Вакер, А. (2002). «Полупроводниковые сверхрешетки: модельная система нелинейного транспорта». Отчеты по физике . 357 (1): 1–7. arXiv : cond-mat/0107207 . Бибкод : 2002PhR...357....1W . CiteSeerX   10.1.1.305.3634 . дои : 10.1016/S0370-1573(01)00029-1 . S2CID   118885849 .
• Хауган, HJ; Шмулович, Ф.; Махалингам, К.; Браун, Дж.Дж.; Мунши, СР; Ульрих, Б. (2005). «Короткопериодические сверхрешетки InAs/GaSb типа II для детекторов среднего инфракрасного диапазона». Письма по прикладной физике . 87 (26): 261106. Бибкод : 2005ApPhL..87z1106H . дои : 10.1063/1.2150269 . [2]

Дальнейшее чтение

• Мендес, Э.Э.; Ублюдок, GR (1993). «Лестницы Ванье-Старка и блоховские колебания в сверхрешетках». Физика сегодня . 46 (6): 34–42. Бибкод : 1993PhT....46f..34M . дои : 10.1063/1.881353 .