ТАК(10)

Схема слабого изоспина W, более слабого изоспина W', сильных g3 и g8 и барионного минус лептонного B зарядов для частиц в модели SO(10), повернута, чтобы показать вложение модели Джорджи – Глэшоу и стандарта. Модель с электрическим зарядом примерно по вертикали. Помимо частиц Стандартной модели, теория включает 30 цветных X-бозонов, ответственных за распад протона , и два W'-бозона.

Схема зарядов частиц в модели SO(10), повернутая, чтобы показать вложение в E6 .

В физике элементарных частиц SO (10) относится к теории великого объединения (GUT), основанной на спиновой группе Spin(10). Сокращенное имя SO(10) является общепринятым. ^[1] среди физиков и происходит от алгебры Ли или, точнее, группы Ли SO (10), которая представляет собой специальную ортогональную группу , дважды покрываемую Spin (10).

SO(10) объединяет модели Джорджи-Глэшоу и Пати-Салама и объединяет все фермионы в поколении в единое поле. Для этого требуется 12 новых калибровочных бозонов в дополнение к 12 из SU(5) и 9 из SU(4)×SU(2)×SU(2) .

История

До появления теории SU(5), лежащей в основе модели Джорджи – Глэшоу , ^[2] Харальд Фрич и Питер Минковски , а также независимо Говард Джорджи обнаружили, что все содержимое материи включено в единое представление, спинориал 16 SO(10). ^[3] Однако стоит отметить, что Георги нашел теорию SO(10) всего за несколько часов до открытия SU(5) в конце 1973 года. ^[4]

Важные подгруппы

Он имеет правила ветвления до [SU(5)×U(1) _χ ]/ Z ₅ .

45\rightarrow 24_{0}\oplus 10_{-4}\oplus {\overline {10}}_{4}\oplus 1_{0}

16\rightarrow 10_{1}\oplus {\bar {5}}_{-3}\oplus 1_{5}

10\rightarrow 5_{-2}\oplus {\bar {5}}_{2}.

Если гиперзаряд содержится в SU (5), это традиционная модель Джорджи-Глэшоу , в которой 16 — это поля материи, 10 — электрослабое поле Хиггса и 24 — внутри 45 — поле Хиггса Великого Общего Теории. Тогда суперпотенциал ; может включать перенормируемые члены вида Tr (45 ⋅ 45) Тр (45 ⋅ 45 ⋅ 45); 10 ⋅ 45 ⋅ 10, 10 ⋅ 16* ⋅ 16 и 16* ⋅ 16. Первые три ответственны за нарушение калибровочной симметрии при низких энергиях и дают массу Хиггса , а два последних дают массы частиц материи и их юкавские связи. к Хиггсу.

Существует еще одно возможное ветвление, при котором гиперзаряд представляет собой линейную комбинацию генератора SU(5) и χ. Это известно как перевернутый SU(5) .

Другая важная подгруппа — это либо [SU(4) × SU(2) _L × SU(2) _R ]/ Z ₂ , либо Z ₂ ⋊ [SU(4) × SU(2) _L × SU(2) _R ]/ Z. ₂ ли лево-правая симметрия в зависимости от того, нарушена , что дает модель Пати-Салама , правило ветвления которой равно

45\rightarrow (15,1,1)\oplus (6,2,2)\oplus (1,3,1)\oplus (1,1,3)

16\rightarrow (4,2,1)\oplus ({\bar {4}},1,2).

Спонтанное нарушение симметрии

Нарушение симметрии SO(10) обычно выполняется с помощью комбинации (( a 45 _H OR a 54 _H ) AND ((a 16 _H AND a ${\overline {16}}_{H}$ ) ИЛИ (a 126 _H И a ${\overline {126}}_{H}$ )) ).

Допустим, мы выбираем _H. 54 Когда это поле Хиггса приобретает масштаб Великого объединения VEV , мы имеем нарушение симметрии до Z ₂ ⋊ [SU(4) × SU(2) _L × SU(2) _R ]/ Z ₂ , т.е. модель Пати–Салама с Z ₂ симметрия слева направо .

Если вместо этого у нас будет 45 _H , это поле Хиггса может приобрести любую VEV в двумерном подпространстве, не нарушая стандартную модель. В зависимости от направления этой линейной комбинации мы можем нарушить симметрию к SU(5)×U(1), модели Джорджи–Глэшоу с U(1) (diag(1,1,1,1,1,- 1,-1,-1,-1,-1)), перевернутый SU(5) (diag(1,1,1,-1,-1,-1,-1,-1,1,1)) , SU(4)×SU(2)×U(1) (diag(0,0,0,1,1,0,0,0,-1,-1)), минимальная лево-правая модель (diag (1,1,1,0,0,-1,-1,-1,0,0)) или SU(3)×SU(2)×U(1)×U(1) для любого другого ненулевого VEV .

Выбор Diag(1,1,1,0,0,-1,-1,-1,0,0) называется механизмом Димопулоса-Вильчека, также известным как «отсутствующий механизм VEV», и он пропорционален B-L .

Выбор 16 _H и a ${\overline {16}}_{H}$ разбивает калибровочную группу до SU(5) Джорджи – Глэшоу. Тот же комментарий относится и к выбору 126 _H и ${\overline {126}}_{H}$ .

Это комбинация ОБА 45/54 и 16/. ${\overline {16}}$ или 126/ ${\overline {126}}$ который разбивает SO(10) на Стандартную модель .

Электрослабый бозон Хиггса и проблема дублет-триплетного расщепления

Электрослабые дублеты Хиггса происходят от SO(10) 10 _H . К сожалению, в этой самой 10 есть и тройки. Массы дублетов должны быть стабилизированы на электрослабом масштабе, который на много порядков меньше, чем масштаб GUT, тогда как триплеты должны быть действительно тяжелыми, чтобы предотвратить распад протона , опосредованный триплетом . См. задачу о расщеплении дублет-триплета .

Среди решений этой проблемы — механизм Димопулоса-Вильчека или выбор Diag(1,1,1,0,0,-1,-1,-1,0,0) из <45>. К сожалению, после 16/ ${\overline {16}}$ или 126/ ${\overline {126}}$ сектор взаимодействует с сектором 45. ^[5]

Содержание

Иметь значение

Представления материи существуют в трех копиях (поколениях) 16-ти представлений. Муфта Юкава 10 _H 16 _f 16 _f . Сюда входит правостороннее нейтрино. Можно либо включить три копии синглетных представлений $φ$ и связь Юкавы. $<{\overline {16}}_{H}>16_{f}\phi$ («двойной качающийся механизм»); или же добавьте взаимодействие Юкавы $<{\overline {126}}_{H}>16_{f}16_{f}$ или добавить неперенормируемую связь $<{\overline {16}}_{H}><{\overline {16}}_{H}>16_{f}16_{f}$ . См. механизм качелей .

Поле 16 _f разветвляется на [SU(5)×U(1) _χ ]/ Z ₅ и SU(4) × SU(2) _L × SU(2) _R как

16\rightarrow 10_{1}\oplus {\bar {5}}_{-3}\oplus 1_{5}

16\rightarrow (4,2,1)\oplus ({\bar {4}},1,2).

Поля датчиков

45 полей разветвляются на [SU(5)×U(1) _χ ]/ Z ₅ и SU(4) × SU(2) _L × SU(2) _R как

45\rightarrow 24_{0}\oplus 10_{-4}\oplus {\overline {10}}_{4}\oplus 1_{0}

45\rightarrow (15,1,1)\oplus (6,2,2)\oplus (1,3,1)\oplus (1,1,3)

и стандартной модели [SU(3) _C × SU(2) _L × U(1) _Y ]/ Z ₆ как

{\begin{aligned}45\rightarrow &(8,1)_{0}\oplus (1,3)_{0}\oplus (1,1)_{0}\oplus \\&(3,2)_{-{\frac {5}{6}}}\oplus ({\bar {3}},2)_{\frac {5}{6}}\oplus \\&(3,1)_{\frac {2}{3}}\oplus ({\bar {3}},1)_{-{\frac {2}{3}}}\oplus (1,1)_{1}\oplus (1,1)_{-1}\oplus (1,1)_{0}\oplus \\&(3,2)_{\frac {1}{6}}\oplus ({\bar {3}},2)_{-{\frac {1}{6}}}.\\\end{aligned}}

Четыре линии — это бозоны SU(3) _C , SU(2) _L и U(1) _B−L ; лептокварки SU (5), которые не меняют заряд X ; лептокварки Пати -Салама SU(2) _R и бозоны ; и новые лептокварки SO(10). (Стандартный электрослабый U(1) _Y представляет собой линейную комбинацию $(1,1) 0$ -бозонов.)

Распад протона

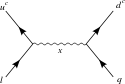
Эти графики относятся к X-бозонам и бозонам Хиггса .
Распад протона измерения 6, опосредованный X- бозоном $(3,2)_{-{\frac {5}{6}}}$ в SU(5) ХОРОШО
Распад протона измерения 6, опосредованный X- бозоном $(3,2)_{\frac {1}{6}}$ в перевернутом SU(5) GUT

Обратите внимание, что SO(10) содержит как SU Джорджи–Глэшоу (5), так и перевернутую SU(5).

Аномалия, свободная от локальных и глобальных аномалий.

Давно известно, что модель SO(10) свободна от всех пертурбативных локальных аномалий, вычислимых с помощью диаграмм Фейнмана. Однако только в 2018 году стало ясно, что модель SO(10) также свободна от всех непертурбативных глобальных аномалий на неспиновых многообразиях — важное правило для подтверждения непротиворечивости теории великого объединения SO(10) со спином. (10) Калибровочная группа и киральные фермионы в 16-мерных спинорных представлениях, определенных на неспиновых многообразиях . ^[6]^[7]

См. также

Перевернутый ТАК(10)

Примечания

^ Баэз, Джон; Уэрта, Джон (11 марта 2010 г.). «Алгебра теорий великого объединения» . Бюллетень Американского математического общества . 47 (3): 483–552. arXiv : 0904.1556 . дои : 10.1090/S0273-0979-10-01294-2 . ISSN 0273-0979 .
^ Джорджи, Ховард; Глэшоу, Шелдон (1974). «Единство всех сил элементарных частиц». Письма о физических отзывах . 32 (8): 438. Бибкод : 1974PhRvL..32..438G . дои : 10.1103/PhysRevLett.32.438 . S2CID 9063239 .
^ Фрич, Х.; Минковский, П. (1975). «Единые взаимодействия лептонов и адронов». Анналы физики . 93 (1–2): 193–266. Бибкод : 1975AnPhy..93..193F . дои : 10.1016/0003-4916(75)90211-0 .
^ Физика, Американский институт (24 сентября 2021 г.). «Говард Джорджи» . www.aip.org . Проверено 12 декабря 2022 г.
^ * Джей Си Баез , Дж. Уэрта (2010). «Алгебра теорий Великого объединения». Бык. Являюсь. Математика. Соц . 47 (3): 483–552. arXiv : 0904.1556 . дои : 10.1090/S0273-0979-10-01294-2 . S2CID 2941843 .
^ Ван, Ювен; Вэнь, Сяо-Ган (1 июня 2020 г.). «Непертурбативное определение стандартных моделей». Обзор физических исследований . 2 (2): 023356. arXiv : 1809.11171 . Бибкод : 2018arXiv180911171W . doi : 10.1103/PhysRevResearch.2.023356 . ISSN 2469-9896 . S2CID 53346597 .
^ Ван, Ювен; Вэнь, Сяо-Ган; Виттен, Эдвард (май 2019 г.). «Новая аномалия SU (2)». Журнал математической физики . 60 (5): 052301. arXiv : 1810.00844 . Бибкод : 2019JMP....60e2301W . дои : 10.1063/1.5082852 . ISSN 1089-7658 . S2CID 85543591 .

[1] Баэз, Джон; Уэрта, Джон (11 марта 2010 г.). «Алгебра теорий великого объединения» . Бюллетень Американского математического общества . 47 (3): 483–552. arXiv : 0904.1556 . дои : 10.1090/S0273-0979-10-01294-2 . ISSN 0273-0979 .

[GG-2] Джорджи, Ховард; Глэшоу, Шелдон (1974). «Единство всех сил элементарных частиц». Письма о физических отзывах . 32 (8): 438. Бибкод : 1974PhRvL..32..438G . дои : 10.1103/PhysRevLett.32.438 . S2CID 9063239 .

[Minkowski1975-3] Фрич, Х.; Минковский, П. (1975). «Единые взаимодействия лептонов и адронов». Анналы физики . 93 (1–2): 193–266. Бибкод : 1975AnPhy..93..193F . дои : 10.1016/0003-4916(75)90211-0 .

[4] Физика, Американский институт (24 сентября 2021 г.). «Говард Джорджи» . www.aip.org . Проверено 12 декабря 2022 г.

[5] * Джей Си Баез , Дж. Уэрта (2010). «Алгебра теорий Великого объединения». Бык. Являюсь. Математика. Соц . 47 (3): 483–552. arXiv : 0904.1556 . дои : 10.1090/S0273-0979-10-01294-2 . S2CID 2941843 .

[1809.11171-6] Ван, Ювен; Вэнь, Сяо-Ган (1 июня 2020 г.). «Непертурбативное определение стандартных моделей». Обзор физических исследований . 2 (2): 023356. arXiv : 1809.11171 . Бибкод : 2018arXiv180911171W . doi : 10.1103/PhysRevResearch.2.023356 . ISSN 2469-9896 . S2CID 53346597 .

[1810.00844-7] Ван, Ювен; Вэнь, Сяо-Ган; Виттен, Эдвард (май 2019 г.). «Новая аномалия SU (2)». Журнал математической физики . 60 (5): 052301. arXiv : 1810.00844 . Бибкод : 2019JMP....60e2301W . дои : 10.1063/1.5082852 . ISSN 1089-7658 . S2CID 85543591 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]