Сингулярная функция

График числа витков карты круга является примером сингулярной функции.

В математике f действительная функция на интервале [ a , b ] называется сингулярной, если она обладает следующими свойствами:

• f непрерывен ] на [ a , b . (**)
• существует множество N меры ) существует и равна нулю , такое, что для всех x вне N производная 0 f   ′ ( x то есть производная f обращается в нуль почти всюду .
• f непостоянна на [ a , b ].

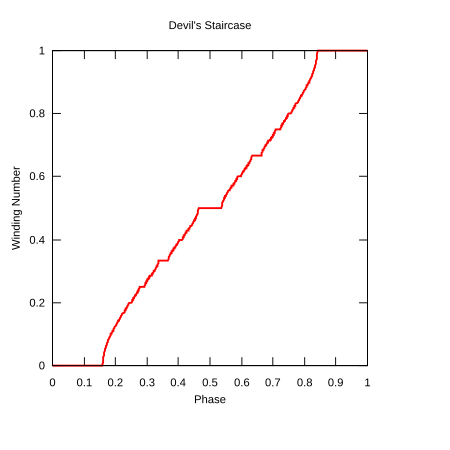
Стандартным примером сингулярной функции является функция Кантора , которую иногда называют дьявольской лестницей (термин, также используемый для сингулярных функций в целом). Однако есть и другие функции, получившие это имя. Один определяется в терминах круговой карты .

Если f ( x ) = 0 для всех x ≤ a и f ( x ) = 1 для всех x ≥ b , то функцию можно использовать для представления кумулятивной функции распределения для случайной величины , которая не является ни дискретной случайной величиной (поскольку вероятность равна нулю для каждой точки) и не является абсолютно непрерывной случайной величиной (поскольку плотность вероятности равна нулю везде, где она существует).

Сингулярные функции возникают, например, как последовательности пространственно модулированных фаз или структур в твердых телах и магнитах , прототипно описываемые моделью Френкеля-Конторовой и моделью ANNNI , а также в некоторых динамических системах . Пожалуй, наиболее известно то, что они лежат в основе дробного квантового эффекта Холла .

При обращении к функциям с особенностью

При обсуждении математического анализа в целом или, более конкретно, реального анализа , комплексного анализа или дифференциальных уравнений , функцию, содержащую математическую особенность , обычно называют «сингулярной функцией». Это особенно верно, когда речь идет о функциях, которые стремятся к бесконечности в точке или на границе. Например, можно сказать: « 1/x становится сингулярной в начале координат, поэтому 1/x — сингулярная функция».

Передовые методы работы с функциями, содержащими особенности, были разработаны в рамках предмета, называемого дистрибутивным или обобщенным функциональным анализом. Определена слабая производная , позволяющая использовать сингулярные функции в уравнениях с частными производными и т. д.

См. также

• Абсолютная непрерывность
• Математическая сингулярность
• Обобщенная функция
• Распределение
• Функция вопросительного знака Минковского

Ссылки

(**) Данное условие зависит от ссылок

• Лебег, Х. (1955–1961), Теория функций действительной переменной , Ф. Унгар
• Халмош, PR (1950), Теория меры , v. Ностранд
• Ройден, HL (1988), Real Analysis , Прентис-Холл, Энглвуд Клиффс, Нью-Джерси
• Лебег, Х. (1928), Уроки интегрирования и поиска примитивных функций , Готье-Виллар