Формализм оператора продукта

Не путать с расширением продукта оператора .

В ЯМР-спектроскопии — формализм оператора произведения это метод, используемый для определения результата последовательности импульсов строгим, но простым способом. С помощью этого метода можно предсказать, как объемная намагниченность будет меняться со временем под действием импульсов, приложенных в разных направлениях. Это чистое улучшение полуклассической векторной модели, которая не способна предсказать многие результаты ЯМР-спектроскопии и представляет собой упрощение полного формализма матрицы плотности.

В этой модели для одного спина существуют четыре базовых оператора: $I_{x}$, $I_{y}$, $I_{z}$ и $E/2$ которые представляют соответственно поляризацию (разницу населенностей между двумя спиновыми состояниями), одноквантовую когерентность (намагниченность в плоскости xy) и единичный оператор. существует множество других неклассических операторов Для связанных систем . Используя этот подход, эволюция намагниченности при свободной прецессии представляется выражением $I_{z}$ и соответствует вращению вокруг оси z с фазовым углом, пропорциональным химическому сдвигу рассматриваемого спина:

$I_{x}{\xrightarrow {\omega \tau I_{z}}}\cos(\omega \tau )I_{x}-\sin(\omega \tau )I_{y}$

Импульсы вокруг осей x и y можно представить как $I_{x}$ и $I_{y}$ соответственно; они позволяют взаимно преобразовывать намагниченность между плоскостями и, в конечном итоге, наблюдать ее в конце последовательности. Поскольку каждый спин будет развиваться по-разному в зависимости от его смещения, с помощью этого формализма можно точно рассчитать, где в конечном итоге окажется намагниченность, и, следовательно, разработать последовательности импульсов для измерения нужного сигнала, исключая при этом другие.

Формализм оператора произведения особенно полезен при описании экспериментов в двумерных измерениях, таких как COSY, HSQC и HMBC.

Мотивация для наборов частиц со спином 1/2

На протяжении всего этого раздела приведенная постоянная Планка $\hbar =1$ для удобства.

Формализм оператора произведения обычно применяется к наборам частиц со спином 1/2 , поскольку тот факт, что отдельные операторы удовлетворяют $L_{x}^{2}=L_{y}^{2}=L_{z}^{2}\propto \mathbf {1}$, где $\mathbf {1}$ является тождественным оператором , делает коммутационные отношения операторов произведения особенно простыми. В принципе этот формализм можно распространить на более высокие спины, но на практике неприводимого сферического тензора чаще используется общая трактовка . Поэтому ниже мы рассматриваем только случай спина 1/2.

Основная идея формализма состоит в том, чтобы облегчить следование оператору плотности системы. $\rho$, который развивается под действием гамильтониана $H$ согласно уравнению Лиувилля-фон Неймана как

${\frac {\partial \rho }{\partial t}}=-\mathrm {i} [H,\rho ].$

Для независимого от времени гамильтониана оператор плотности наследует свои решения от оператора эволюции времени Шредингера $U(t)=\exp(-\mathrm {i} Ht)$ как

$\rho (t)=U(t)\,\rho (0)\,U^{-1}(t)=\exp(-\mathrm {i} Ht)\,\rho (0)\,\exp(+\mathrm {i} Ht)$

Двойственность оператора-состояния плотности

Предположим, что один спин-1/2 $L$ находится в штате $|\uparrow \,\rangle$, которое является собственным состоянием оператора z-спина $L_{z}$, то есть $L_{z}|\uparrow \,\rangle ={\frac {1}{2}}|\uparrow \,\rangle$. Сходным образом $L_{z}|\downarrow \,\rangle =-{\frac {1}{2}}|\downarrow \,\rangle$. Используя разложение эрмитова оператора $A$ в терминах проекций на свои собственные сети $|a\rangle$ с собственными значениями $a$ как $A=\sum a|a\rangle \langle a|$, соответствующий оператор плотности

${\begin{aligned}\rho _{|\uparrow \,\rangle }&=|\uparrow \,\rangle \langle \,\uparrow |\\&={\frac {1}{2}}(|\uparrow \,\rangle \langle \,\uparrow |+|\downarrow \,\rangle \langle \,\downarrow |)+{\frac {1}{2}}(|\uparrow \,\rangle \langle \,\uparrow |-|\downarrow \,\rangle \langle \,\downarrow |)\\&={\frac {1}{2}}\mathbf {1} +L_{z},\end{aligned}}$

где $\mathbf {1}$ является идентификационным оператором. Аналогично, оператор плотности состояния $|\downarrow \,\rangle$ является

$\rho _{|\downarrow \,\rangle }={\frac {1}{2}}\mathbf {1} -L_{z}$

Поскольку спиновые операторы $L_{x},L_{y},L_{z}$ все они бесследны , а математическое ожидание оператора $A$ для системы с оператором плотности $\rho$ является $\langle A\rangle =\operatorname {tr} (\rho A)$, члены, пропорциональные единичному оператору $\mathbf {1}$ не влияют на ожидания спиновых операторов. Кроме того, эти части не меняются во времени, поскольку они тривиально коммутируют с гамильтонианом. Следовательно, эти условия можно игнорировать, и состояние $|\uparrow \,\rangle$ соответствует оператору плотности $+L_{z}$, в то время как государство $|\downarrow \,\rangle$ соответствует оператору плотности $-L_{z}$. Точно так же поляризация вдоль положительной оси x, то есть состояние $|\uparrow _{x}\,\rangle$, соответствует оператору плотности $+L_{x}$. Эта идея естественным образом распространяется на множественные спины, где состояния и операторы являются прямыми продуктами односпиновых состояний и операторов. Следовательно, операторные члены в операторе плотности имеют прямую двойственность с состояниями.

В случае двух вращений $L,S$члены оператора плотности (игнорируя тождество само по себе) можно интерпретировать как представляющие

• $L_{z},S_{z}$ - продольная намагниченность
• $L_{x},L_{y},S_{x},S_{y}$ - синфазная поперечная намагниченность, которая является наблюдаемой величиной в ЯМР.
• $2L_{x}S_{z},2L_{y}S_{z},2L_{z}S_{x},2L_{z}S_{y}$ - противофазное продольное намагничивание
• $2L_{z}S_{z}$ - продольный двухспиновый порядок
• $2L_{x}S_{x},2L_{x}S_{y},2L_{y}S_{x},2L_{y}S_{y}$ - другие связи, которые труднее интерпретировать, но которые могут трансформироваться в другие термины.

где например $L_{z}$ это сокращение от произведения Кронекера. $L_{z}\otimes \mathbf {1} _{S}$, где $\mathbf {1} _{S}$ является идентификационным оператором на $S$ вращение и аналогично $L_{x}S_{z}$ это сокращение от $L_{x}\otimes S_{z}$.

Множители два в «истинных» двухспиновых операторах должны обеспечить удобные коммутационные соотношения в этом конкретном случае спина 1/2 - см. ниже. Обратите также внимание, что вместо этого мы могли бы расширить оператор плотности в базисе $L_{z},L_{\pm }=L_{x}\pm \mathrm {i} \,L_{y}$ и т. д., где поперечные операторы были заменены операторами повышения и понижения . При квадратурном обнаружении наблюдаемая, связанная с отдельным спином, фактически является неэрмитовой $L_{\pm }$, поэтому иногда это удобнее.

Эволюция оператора плотности

Рассмотрим операторы $A,B,C$ подчиняющиеся циклическим коммутационным соотношениям

${\begin{aligned}\left.[A,B]\right.&=\mathrm {i} C,\\\left.[B,C]\right.&=\mathrm {i} A,\\\left.[C,A]\right.&=\mathrm {i} B.\end{aligned}}$

Фактически для следующего вывода необходимы только первые два соотношения, но поскольку мы обычно работаем с операторами, связанными с декартовыми направлениями, такими как отдельные операторы углового момента, третий коммутатор следует за аргументом симметрии.

коммутации Введем также супероператор ${\hat {F}}$ оператора $F$ (в нашем случае это более формально связано с присоединенным представлением алгебры Ли, элементами которой являются $A,B,C$), который действует как

${\hat {F}}\,\bullet =[F,\bullet ]$

В частности, для циклических операторов имеем

${\begin{aligned}{\hat {B}}A&=[B,A]=-\mathrm {i} C,\\{\hat {B}}^{2}A&=[B,[B,A]]=[B,-\mathrm {i} C]=-\mathrm {i} [B,C]=A,\end{aligned}}$

и, следовательно, для целого числа $n\geq 0$

${\begin{aligned}{\hat {B}}^{2n}A&=A,\\{\hat {B}}^{2n+1}A&=-\mathrm {i} C.\end{aligned}}$

Идентичность для двух операторов $F,G$ является

$\exp(F)G\exp(-F)=\exp({\hat {F}})G,$

которое можно получить, положив $F\to tF$ где $t$ является скалярным параметром, дифференцирующим обе части по отношению к $t$и отмечая, что обе стороны удовлетворяют одному и тому же дифференциальному уравнению по этому параметру с одинаковыми начальными условиями при $t=0$. В частности, для некоторого скалярного параметра $\theta$, у нас есть

${\begin{aligned}\exp(-\mathrm {i} \theta B)A\exp(+\mathrm {i} \theta B)&=\exp(-\mathrm {i} \theta {\hat {B}})A\\&=\sum _{n=0}^{\infty }{\frac {(-\mathrm {i} \theta )^{n}}{n!}}{\hat {B}}^{n}A\\&=\sum _{n=0}^{\infty }\left[{\frac {(-\mathrm {i} \theta )^{2n}}{(2n)!}}\,A+{\frac {(-\mathrm {i} \theta )^{2n+1}}{(2n+1)!}}\cdot -\mathrm {i} C\right]\\&=A\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}\theta ^{2n}-C\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\\&=\cos \theta \,A-\sin \theta \,C,\end{aligned}}$

( 1 )

где окончательное равенство следует из признания ряда Тейлора для синуса и косинуса. Теперь предположим, что оператор плотности в нулевой момент времени равен $\rho (0)=A$, и ему разрешено свободно развиваться под действием гамильтониана $H=\alpha \,B$ где $\alpha$ является неким скаляром. Используя приведенные выше результаты, оператор плотности в некоторое позднее время $t$ будет предоставлен

$\rho (t)=\exp(-\mathrm {i} \alpha t\,B)A\exp(+\mathrm {i} \alpha t\,B)=\cos \alpha t\,A-\sin \alpha t\,C.$

( 2 )

Интерпретация этого заключается в том, что, хотя сам угловой момент ядерного спина не связан с вращениями в трехмерном пространстве так же, как угловой момент, эволюцию оператора плотности можно рассматривать как вращения в абстрактном пространстве, в котором операторы $A,B,C$ являются генераторами вращений вокруг осей. Примером такого набора генераторов являются как раз операторы спина $L_{x},L_{y},L_{z}$ сами себя.

Теперь мы также вводим «стрелочную нотацию», обычно используемую в ЯМР, которая описывает общую эволюцию, приведенную выше, как сокращение.

$A\xrightarrow {\alpha \,Bt} \cos \alpha t\,A-\sin \alpha t\,C$.

Если говорить более конкретно о радиочастотных импульсах, применяемых во время экспериментов ЯМР, то жесткий импульс с углом кончика $\theta$ вокруг направления $q$ написано как $(\theta )_{q}$ над стрелкой и соответствует взятию $B=L_{q}$ в качестве генератора вращения в уравнении 1 . Если нет двусмысленности, метка стрелки может быть опущена или вместо нее может быть, например, текстом.

Обратите внимание, что более сложные вычисления теперь сведены к более простой процедуре, не требующей знания базовой квантовой механики, тем более что подпространства циклических операторов можно заранее свести в таблицы.

Примеры

Импульс перефокусировки на 180°

Гамильтониан для одного спина $L$ развивается при химическом сдвиге угловой частоты $\omega$ является

$H=\omega L_{z},$

это означает, что в ансамбле многих таких спинов с несколько разными химическими сдвигами происходит дефазировка намагниченности в $x$- $y$ самолет. Рассмотрим импульсную последовательность

$\left({\frac {\pi }{2}}\right)_{x}$ — $\tau$ — $(\pi )_{x}$ — $\tau ,$

где $\tau$ представляет собой временной интервал. Начиная с состояния равновесия со всей поляризацией вдоль $z$-ось, эволюция отдельного спина в ансамбле

${\begin{aligned}L_{z}\xrightarrow {\left({\frac {\pi }{2}}\right)_{x}} -L_{y}\xrightarrow {\omega L_{z}t} -L_{y}\cos \omega t+L_{x}\sin \omega t\xrightarrow {(\pi )_{x}} L_{y}\cos \omega t+L_{x}\sin \omega t\xrightarrow {\omega L_{z}t} &(L_{y}\cos \omega t-L_{x}\sin \omega t)\cos \omega t+(L_{x}\cos \omega t+L_{y}\sin \omega t)\sin \omega t\\&=L_{y}(\cos ^{2}\omega t+\sin ^{2}\omega t)+L_{x}(-\sin \omega t\cos \omega t+\cos \omega t\sin \omega t)\\&=L_{y}.\end{aligned}}$

Следовательно, эта последовательность перефокусирует поперечную намагниченность, создаваемую первым импульсом, независимо от величины химического сдвига.

В качестве доказательства полезности формализма предположим, что вместо этого мы попытались достичь того же результата, используя только состояния и, следовательно, операторы эволюции во времени Шредингера. Это равносильно попытке упростить унитарный пропагатор $U$ принимая исходное состояние $|\psi _{0}\rangle$до конечного состояния $|\psi \rangle$ как $|\psi \rangle =U|\psi _{0}\rangle$, где явно

$U=\exp(-\mathrm {i} \omega L_{z}t)\exp(-\mathrm {i} \pi L_{x})\exp(-\mathrm {i} \omega L_{z}t).$

По сути, мы хотим найти пропагатор в виде $U=\exp C$, то есть как одна экспонента комбинации операторов, потому что это дает эффективный гамильтониан, действующий во время последовательности. Поскольку аргументы экспонент в исходной форме пропагатора не коммутируют, это равнозначно решению конкретного примера проблемы Бейкера – Кэмпбелла – Хаусдорфа (БЧ). В этом относительно простом случае мы можем решить проблему BCH, используя тот факт, что $Uf(A)U^{\dagger }=f(UAU^{\dagger })$ для унитарного оператора $U$, оператор $A$ и функция $f$, а также математическое сходство операторов спина с генераторами физического вращения, позволяющее записать

$\exp(\mathrm {i} \pi L_{x})\exp(-\mathrm {i} \omega L_{z}t)\exp(-\mathrm {i} \pi L_{x})=\exp \left[-\mathrm {i} \omega t\exp(\mathrm {i} \pi L_{x})L_{z}\exp(-\mathrm {i} \pi L_{x})\right]=\exp(\mathrm {i} \omega L_{z}t)\implies \exp(-\mathrm {i} \omega L_{z}t)\exp(-\mathrm {i} \pi L_{x})=\exp(-\mathrm {i} \pi L_{x})\exp(\mathrm {i} \omega L_{z}t).$

Следовательно $U=\exp(-\mathrm {i} \pi L_{x})$ и остается только эффект импульса 180°, что согласуется с подходом оператора продукта. Для более крупных последовательностей импульсов такая обработка состояний быстро становится еще более громоздкой, если не более продвинутые методы, такие как точная эффективная теория Гамильтона (которая дает выражения в замкнутой форме для запутанных пропагаторов с помощью теоремы Кэли-Гамильтона используются и собственных разложений).

Амплитуда эха Хана в неоднородном магнитном поле

В качестве расширения рассмотренного выше импульса рефокусировки рассмотрим набор из двух импульсов с произвольными углами поворота. $\alpha _{1}$ и $\alpha _{2}$, это последовательность

$\left(\alpha _{1}\right)_{x}$ — $\tau$ — $\left(\alpha _{2}\right)_{x}$ — $\tau ,$

где снова $\tau$ представляет собой временной интервал. Свободный отказ от ненужных терминов, эволюция одного вращения со смещением $\omega$ сразу после второго импульса

$L_{z}\xrightarrow {\left(\alpha _{1}\right)_{x}} -L_{y}\sin \alpha _{1}+\cdots \xrightarrow {\omega L_{z}t} -L_{y}\sin \alpha _{1}\cos \omega t+L_{x}\sin \alpha _{1}\sin \omega t+\cdots \xrightarrow {\left(\alpha _{2}\right)_{x}} L_{x}\sin \alpha _{1}\sin \omega t-L_{y}\sin \alpha _{1}\cos \alpha _{2}\cos \omega t+\cdots .$

Теперь рассмотрим ансамбль спинов в магнитном поле, достаточно неоднородном, чтобы полностью дефазировать спины в интервале между импульсами. После второго импульса мы можем разложить оставшиеся члены в сумму двух спиновых населенностей, отличающихся только знаком $L_{y}$ термин в том смысле, что для отдельного спина мы имеем

$L_{x}\sin \omega t-\cos \alpha _{2}\,L_{y}\cos \omega t=\cos ^{2}{\frac {\alpha _{2}}{2}}\,(L_{x}\sin \omega t-L_{y}\cos \omega t)+\sin ^{2}{\frac {\alpha _{2}}{2}}\,(L_{x}\sin \omega t+L_{y}\cos \omega t),$

где мы использовали тождества $\cos ^{2}\theta +\sin ^{2}\theta =1$ и $\cos ^{2}\theta -\sin ^{2}\theta =\cos 2\theta$.

Это спины в новой популяции, порожденные вторым импульсом, а именно с $+L_{y}$, что приведет к образованию эха после эволюции для следующего $\tau$ интервал. Поэтому, не забывая включать $\sin \alpha _{1}$ Внесенный первым импульсом, амплитуда результирующего эха Хана относительно амплитуды, создаваемой идеальной последовательностью импульсов рефокусировки 90–180°, примерно равна

$\sin \alpha _{1}\sin ^{2}{\frac {\alpha _{2}}{2}}.$

Обратите внимание, что это не точный результат, поскольку он учитывает только перефокусировку поляризации, которая была поперечной непосредственно перед вторым импульсом. В действительности будут дополнительные поперечные компоненты, возникающие из-за изменения продольной намагниченности, оставшейся после первого импульса. Однако для многих углов вершины это хорошее практическое правило.

Чтобы вместо этого прийти к этому результату с использованием формализма состояний, нам пришлось бы нетривиально вычислить пропагатор вращения как

$U(\alpha )=\exp(-\mathrm {i} \alpha L_{x})=\cos {\frac {\alpha }{2}}\,\mathbf {1} -2\mathrm {i} \sin {\frac {\alpha }{2}}\,L_{x},$

а затем оценить вероятность перехода, рассматривая результат применения этого значения к состоянию, представляющему поляризацию в поперечной плоскости.

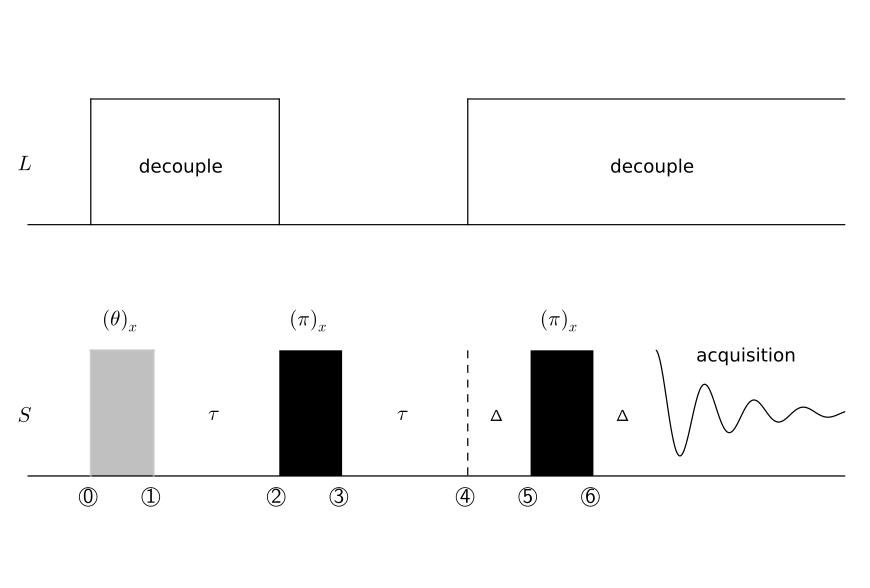
DEPT (улучшение без искажений за счет переноса поляризации)

DEPT (улучшение без искажений за счет переноса поляризации) — это последовательность импульсов, используемая для различения кратности водородных связей с углеродом, то есть она может разделять _{C, CH, CH 2} и CH ₃ группы . Это достигается за счет использования гетероядерной связи углерод-водород. $J$- соединение и изменение угла вершины конечного импульса в последовательности. Основная последовательность импульсов показана ниже.

В предположении слабой связи члены химического сдвига коммутируют с $J$-связывающий член в гамильтониане. Следовательно, мы можем игнорировать рефокусированный химический сдвиг (см . § Импульс рефокусировки на 180° ) в двух интервалах, содержащих $\pi$-импульсы, а именно $(1)\to (4)$ и $(3)\to (6)$, и дополнительно воздержитесь от оценки эволюции химического сдвига за последние ${\frac {\tau }{2}}$ период $(5)\to (6)$. Время разделения импульсов ${\frac {\tau }{2}}$ настраивается на силу сцепления $J$ (с соответствующим коэффициентом Гамильтона $\alpha =\pi J$) такой, что он удовлетворяет

${\frac {\tau }{2}}\cdot \pi J={\frac {\pi }{2}}\implies \tau ={\frac {1}{J}}$,

потому что тогда первый член в эволюционном операторе плотности в уравнении 2 исчезает при эволюции чистой связи между импульсами.

СН

Обозначим спин водорода как $L$, а спин углерода на $S$. Для наглядности предположим, что состояние равновесия имеет поляризацию только на $L$-спин (в действительности на $S$ спин, причем относительные населенности определяются тепловыми факторами Больцмана ). $J$-связывающий гамильтониан

$H=\pi J\,2L_{z}S_{z}$

что дает следующую эволюцию

${\begin{aligned}(0)&:\ L_{z}\\(0)\to (1)&:\ L_{z}\xrightarrow {\left({\frac {\pi }{2}}\right)_{xL}} -L_{y}\\(1)\to (2)&:\ {-L_{y}}\xrightarrow {J-{\text{coup.}}} 2L_{x}S_{z}\\(2)\to (3)&:\ 2L_{x}S_{z}\xrightarrow {\left({\frac {\pi }{2}}\right)_{xS}} -2L_{x}S_{y}\xrightarrow {\left(\pi \right)_{xL}} -2L_{x}S_{y}\\(3)\to (4)&:\ {-2L_{x}S_{y}}\xrightarrow {J-{\text{coup.}}} {-2L_{x}S_{y}}\\(4)\to (5)&:\ {-2L_{x}S_{y}}\xrightarrow {\left(\pi \right)_{xS}} 2L_{x}S_{y}\xrightarrow {(\theta )_{yL}} 2L_{x}S_{y}\cos \theta -2L_{z}S_{y}\sin \theta \\(5)\to (6)&:\ {2L_{x}S_{y}\cos \theta -2L_{z}S_{y}\sin \theta }\xrightarrow {J-{\text{coup.}}} 2L_{x}S_{y}\cos \theta +S_{x}\sin \theta \end{aligned}}$

Нетривиальные коммутаторы, используемые для идентификации циклического подпространства для $(1)\to (2)$ являются

${\begin{aligned}\left.[L_{y},2L_{z}S_{z}]\right.&=2(L_{y}\otimes \mathbf {1} _{L})(L_{z}\otimes S_{z})-2(L_{z}\otimes S_{z})(L_{y}\otimes \mathbf {1} _{L})\\&=2L_{y}L_{z}\otimes S_{z}-2L_{z}L_{y}\otimes S_{z}\\&=2[L_{y},L_{z}]\otimes S_{z}\\&=\mathrm {i} 2L_{x}S_{z},\end{aligned}}$

и, следовательно, следующее циклическое вращение

${\begin{aligned}\left.[2L_{z}S_{z},2L_{x}S_{z}]\right.&=4[L_{z},L_{x}]\otimes S_{z}^{2}\\&=4\mathrm {i} \,L_{y}\otimes {\frac {1}{4}}\mathbf {1} _{S}\\&=\mathrm {i} L_{y},\end{aligned}}$

где мы использовали «идентичность смешанного продукта» $(A\otimes B)(C\otimes D)=AC\otimes BD$, который связывает матрицу и произведение Кронекера для совместимых размеров $A,B,C,D$, а также тот факт, что поскольку два собственных значения любого из операторов спина 1/2 $S_{x},S_{y},S_{z}$ являются $s=\pm {\frac {1}{2}}$, любой из их квадратов определяется выражением $s^{2}\mathbf {1} _{S}$ по теореме Кэли-Гамильтона .

Отметим также, что $2L_{x}L_{y}$ термин инвариантен относительно $J$- эволюция сцепления. То есть этот член коммутирует с гамильтонианом, и в данном случае это можно подтвердить вручную, вычислив коммутатор $[2L_{x}L_{y},2L_{z}S_{z}]=0$ используя матричные представления операторов спина.

СН ₂

Теперь обозначим два спина водорода как $L,L'$ и спин углерода на $S$. $J$-связывающий гамильтониан теперь

$H=\pi J(2L_{z}S_{z}+2L_{z}'S_{z})$

что дает следующую эволюцию

${\begin{aligned}(0)&:\ L_{z}+L_{z}'\\(0)\to (1)&:\ L_{z}+L_{z}'\xrightarrow {\left({\frac {\pi }{2}}\right)_{xL}} -L_{y}+L_{z}'\xrightarrow {\left({\frac {\pi }{2}}\right)_{xL'}} -L_{y}-L_{y}'\\(1)\to (2)&:\ {-L_{y}-L_{y}'}\xrightarrow {J-{\text{coup.}}} 2L_{x}S_{z}+2L_{x}'S_{z}\\(2)\to (3)&:\ 2L_{x}S_{z}+2L_{x}'S_{z}\xrightarrow {\left({\frac {\pi }{2}}\right)_{xS}} -2L_{x}S_{y}-2L_{x}'S_{y}\xrightarrow {\left(\pi \right)_{xL}} -2L_{x}S_{y}-2L_{x}'S_{y}\xrightarrow {\left(\pi \right)_{xL'}} -2L_{x}S_{y}-2L_{x}'S_{y}\\(3)\to (4)&:\ -2L_{x}S_{y}-2L_{x}'S_{y}\xrightarrow {J-{\text{coup.}}} 4L_{x}L_{z}'S_{x}+4L_{z}L_{x}'S_{x}\\(4)\to (5)&:\ 4L_{x}L_{z}'S_{x}+4L_{z}L_{x}'S_{x}\xrightarrow {\left(\pi \right)_{xS}} 4L_{x}L_{z}'S_{x}+4L_{z}L_{x}'S_{x}\xrightarrow {(\theta )_{yL}} 4L_{z}L_{x}'S_{x}\cos \theta -4L_{z}L_{z}'S_{x}\sin \theta +{\text{others}}\xrightarrow {(\theta )_{yL'}} -8L_{z}L_{z}'S_{x}\cos \theta \sin \theta +{\text{others}}\\(5)\to (6)&:\ -8L_{z}L_{z}'S_{x}\cos \theta \sin \theta +{\text{others}}\xrightarrow {J_{LS}-{\text{coup.}}} -4L_{z}'S_{y}\cos \theta \sin \theta +{\text{others}}\xrightarrow {J_{L'S}-{\text{coup.}}} 2S_{x}\cos \theta \sin \theta +{\text{others}}\end{aligned}}$

где «другие» обозначают различные термины, которые можно безопасно игнорировать, поскольку они не превратятся в наблюдаемую поперечную поляризацию на целевом спине. $S$. Необходимые циклические коммутаторы для работы с $J$-эволюция связи - это следующие три набора (и их $L\leftrightarrow L'$ версии при необходимости)

${\begin{aligned}\left.[L_{x}S_{y},2L_{z}'S_{z}]\right.&=2L_{x}\otimes L_{z}'\otimes [S_{y},S_{z}]\\&=\mathrm {i} \,2L_{x}L_{z}'S_{x}\end{aligned}}$

${\begin{aligned}\left.[2L_{z}'S_{z},2L_{x}L_{z}'S_{x}]\right.&=4L_{x}\otimes {L_{z}'}^{2}\otimes [S_{z},S_{x}]\\&=4L_{x}\otimes {\frac {1}{4}}\mathbf {1} _{L'}\otimes \mathrm {i} S_{y}\\&=\mathrm {i} L_{x}S_{y},\end{aligned}}$

${\begin{aligned}\left.[2L_{z}L_{z}'S_{x},2L_{z}S_{z}]\right.&=4L_{z}^{2}\otimes L_{z}'\otimes [S_{x},S_{z}]\\&=4\cdot {\frac {1}{4}}\mathbf {1} _{L}\otimes L_{z}'\otimes -\mathrm {i} S_{y}\\&=\mathrm {i} \cdot -L_{z}'S_{y}\end{aligned}}$

${\begin{aligned}\left.[2L_{z}L_{z},-L_{z}'S_{y}]\right.&=-L_{z}\otimes L_{z}'\otimes [S_{z},S_{y}]\\&=\mathrm {i} \,2L_{z}L_{z}'S_{x},\end{aligned}}$

${\begin{aligned}\left.[2L_{z}'S_{y},2L_{z}'S_{z}]\right.&=4\mathbf {1} _{L}\otimes L_{z}'^{2}\otimes [S_{y},S_{z}]\\&=4\mathbf {1} _{L}\otimes {\frac {1}{4}}\mathbf {1} _{L'}\otimes \mathrm {i} S_{x}\\&=\mathrm {i} S_{x}\end{aligned}}$

${\begin{aligned}\left.[2L_{z}'S_{z},S_{x}]\right.&=2\mathbf {1} _{L}\otimes L_{z}'\otimes [S_{z},S_{x}]\\&=\mathrm {i} \,2L_{z}'\otimes S_{y}.\end{aligned}}$

CH_CH3

Аналогичное (но более длительное) рассмотрение дает окончательный наблюдаемый член как $3S_{x}\cos ^{2}\theta \sin \theta$.

APT (прикрепленный протонный тест)

см. в § DEPT (улучшение без искажений за счет переноса поляризации) Обозначения, используемые в этом примере, .

APT похож на DEPT в том, что он определяет кратность углерода. Однако он имеет дополнительные вырождения: он дает одинаковые положительные сигналы для C и CH ₂ и одинаковые отрицательные сигналы для CH и CH ₃ . Один из вариантов базовой последовательности импульсов показан ниже.

Ключевое наблюдение заключается в том, что, поскольку мы снова можем игнорировать перефокусированный химический сдвиг, единственная значимая динамика происходит в интервале без разделения водорода, где мы можем рассматривать исключительно $J$-муфта. Используя интервал вдвое длиннее, чем в случае DEPT, мы гарантируем, что оператор плотности $L_{y}$ в начале интервала просто меняется знак после связи (поскольку это соответствует $\alpha t=\pi$ в общем лечении и $\cos \pi =-1,\,\sin \pi =0$). Гамильтонианы для связей с каждым из $n$ отдельные соседние атомы водорода коммутируют, поэтому общий эффект умножается на коэффициент $(-1)^{n}$. Этим и объясняется переменный знак сигнала, упомянутый выше.

Ссылки

• Джеймс Килер. «Понимание ЯМР-спектроскопии» (перепечатано в Кембриджском университете ) . Калифорнийский университет в Ирвайне . Проверено 5 августа 2012 г.
• Дэвид Донн; Дэвид Горенштейн. «Иллюстрированное изображение формализма оператора продукта» (PDF) . Техасский университет . Архивировано из оригинала (PDF) 14 мая 2013 г. Проверено 5 августа 2012 г.
• Хенниг, Юрген (1991). «Эхо - как генерировать, распознавать, использовать или избегать их в последовательностях МР-изображений. Часть I: Фундаментальные и не очень фундаментальные свойства спинового эха». Концепции магнитного резонанса . 3 (3): 125–143. дои : 10.1002/cmr.1820030302 .
• Матееску, Георге Д; Валериу, Адриан (1993). «Матрица плотности 2D ЯМР и обработка продукта оператором». Журнал химического образования . 70 (6): А172. Бибкод : 1993JChEd..70S.172. . дои : 10.1021/ed070pA172.3 .
• Симинович, Дэвид; Унтидт, Томас; Нильсен, Нильс Хр. (2004). «Точная эффективная теория Гамильтона. II. Полиномиальное разложение матричных функций и запутанных унитарных экспоненциальных операторов». Журнал химической физики . 120 (1): 51–66. Бибкод : 2004ЖЧФ.120...51С . дои : 10.1063/1.1628216 . ПМИД   15267261 .
• Чжан, Юнин; Хан, Фей; Ершов, Алексей (2013). «Формализм оператора продукта». EMag Рес . дои : 10.1002/9780470034590.emrstm1310 . ISBN  978-0470034590 .